


高考数学一轮复习课时作业:50 圆的方程 Word版含解析
展开 课时作业50 圆的方程
课时作业50 圆的方程
一、选择题
1.已知圆C的圆心是直线x-y+1=0与x轴的交点,且圆C与直线x+y+3=0相切,则圆C的方程是( A )
A.(x+1)2+y2=2 B.(x+1)2+y2=8
C.(x-1)2+y2=2 D.(x-1)2+y2=8
解析:直线x-y+1=0与x轴的交点为(-1,0).根据题意,圆C的圆心坐标为(-1,0).因为圆与直线x+y+3=0相切,所以半径为圆心到切线的距离,即r=d==,则圆的方程为(x+1)2+y2=2.故选A.
2.(2019·河北邯郸联考)以(a,1)为圆心,且与两条直线2x-y+4=0与2x-y-6=0同时相切的圆的标准方程为( A )
A.(x-1)2+(y-1)2=5
B.(x+1)2+(y+1)2=5
C.(x-1)2+y2=5
D.x2+(y-1)2=5
解析:因为两平行直线2x-y+4=0与2x-y-6=0的距离为d==2.故所求圆的半径为r=,所以圆心(a,1)到直线2x-y+4=0的距离为=,即a=1或a=-4.又因为圆心(a,1)到直线2x-y-6=0的距离也为r=,所以a=1.因此所求圆的标准方程为(x-1)2+(y-1)2=5.故选A.
3.已知直线l:x+my+4=0,若曲线x2+y2+6x-2y+1=0上存在两点P,Q关于直线l对称,则m的值为( D )
A.2 B.-2
C.1 D.-1
解析:因为曲线x2+y2+6x-2y+1=0表示的是圆,其标准方程为(x+3)2+(y-1)2=9,若圆(x+3)2+(y-1)2=9上存在两点P,Q关于直线l对称,则直线l:x+my+4=0过圆心(-3,1),所以-3+m+4=0,解得m=-1.
4.(2019·贵阳市监测考试)经过三点A(-1,0),B(3,0),C(1,2)的圆与y轴交于M,N两点,则|MN|=( A )
A.2 B.2
C.3 D.4
解析:根据A,B两点的坐标特征可知圆心在直线x=1上,设圆心为P(1,m),则半径r=|m-2|,所以(m-2)2=22+m2,解得m=0,所以圆心为P(1,0),所以圆的方程为(x-1)2+y2=4,当x=0时,y=±,所以|MN|=2.
5.(2019·西安八校联考)若过点A(3,0)的直线l与曲线(x-1)2+y2=1有公共点,则直线l斜率的取值范围为( D )
A.(-,) B.[-,]
C.(-,) D.[-,]
解析:解法1:数形结合可知,直线l的斜率存在,设直线l的方程为y=k(x-3),则圆心(1,0)到直线y=k(x-3)的距离应小于等于半径1,即≤1,解得-≤k≤,故选D.
解法2:数形结合可知,直线l的斜率存在,设为k,当k=1时,直线l的方程为x-y-3=0,圆心(1,0)到直线l的距离为=>1,直线与圆相离,故排除A,B;当k=时,直线l的方程为x-y-3=0,圆心(1,0)到直线l的距离为=1,直线与圆相切,排除C,故选D.
6.(2019·河南豫西五校联考)在平面直角坐标系xOy中,以点(0,1)为圆心且与直线x-by+2b+1=0相切的所有圆中,半径最大的圆的标准方程为( B )
A.x2+(y-1)2=4 B.x2+(y-1)2=2
C.x2+(y-1)2=8 D.x2+(y-1)2=16
解析:直线x-by+2b+1=0过定点P(-1,2),如图.
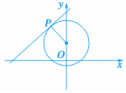
∴圆与直线x-by+2b+1=0相切于点P时,圆的半径最大,为,此时圆的标准方程为x2+(y-1)2=2,故选B.
二、填空题
7.已知圆C的圆心在x轴的正半轴上,点M(0,)在圆C上,且圆心到直线2x-y=0的距离为,则圆C的方程为(x-2)2+y2=9.
解析:因为圆C的圆心在x轴的正半轴上,设C(a,0),且a>0,所以圆心到直线2x-y=0的距离d==,解得a=2,
所以圆C的半径r=|CM|==3,
所以圆C的方程为(x-2)2+y2=9.
8.(2019·贵阳市摸底考试)过点M(2,2)的直线l与坐标轴的正方向分别相交于A,B两点,O为坐标原点,若△OAB的面积为8,则△OAB外接圆的标准方程是(x-2)2+(y-2)2=8.
解析:设直线l的方程为+=1(a>0,b>0),由直线l过点M(2,2),得+=1.又S△OAB=ab=8,所以a=4,b=4,所以△OAB是等腰直角三角形,且M是斜边AB的中点,则△OAB外接圆的圆心是点M(2,2),半径|OM|=2,所以△OAB外接圆的标准方程是(x-2)2+(y-2)2=8.
9.(2019·湖南湘东五校联考)圆心在抛物线y=x2(x<0)上,且和该抛物线的准线及y轴都相切的圆的标准方程为(x+1)2+(y-)2=1.
解析:依题意设圆的方程为(x-a)2+(y-a2)2=r2(a<0),又该圆与抛物线的准线及y轴均相切,所以+a2=r=-a⇒故所求圆的标准方程为(x+1)2+(y-)2=1.
三、解答题
10.已知以点P为圆心的圆经过点A(-1,0)和B(3,4),线段AB的垂直平分线交圆P于点C和D,且|CD|=4.
(1)求直线CD的方程;
(2)求圆P的方程.
解:(1)由题意知,直线AB的斜率k=1,中点坐标为(1,2).
则直线CD的方程为y-2=-(x-1),
即x+y-3=0.
(2)设圆心P(a,b),
则由点P在CD上得a+b-3=0. ①
又∵直径|CD|=4,∴|PA|=2,
∴(a+1)2+b2=40. ②
由①②解得或
∴圆心P(-3,6)或P(5,-2).
∴圆P的方程为(x+3)2+(y-6)2=40或(x-5)2+(y+2)2=40.
11.(2019·山西长治六校联考)已知圆C经过点A,B,直线x=0平分圆C,直线l与圆C相切,与圆C1:x2+y2=1相交于P,Q两点,且满足OP⊥OQ.
(1)求圆C的方程;
(2)求直线l的方程.
解:(1)依题意知圆心C在y轴上,可设圆心C的坐标为(0,b),圆C的方程为x2+(y-b)2=r2(r>0).
因为圆C经过A,B两点,所以2+2=2+2,
即+-b+b2=+-b+b2,解得b=4.
又易知r2=2+2=,
所以圆C的方程为x2+(y-4)2=.
(2)当直线l的斜率不存在时,由l与C相切得l的方程为x=±,此时直线l与C1交于P,Q两点,不妨设P点在Q点的上方,则P,,Q,-或P-,,Q,则·=0,所以OP⊥OQ,满足题意.
当直线l的斜率存在时,易知其斜率不为0,
设直线l的方程为y=kx+m(k≠0,m≠0),
∵OP⊥OQ且C1的半径为1,
∴O到l的距离为,
又l与圆C相切,∴
由①②知|m|=|m-4|,∴m=2,
代入①得k=±,
∴l的方程为y=±x+2.
综上,l的方程为x=±或y=±x+2.
12.(2019·江西新余五校联考)已知圆O:x2+y2=9,过点C(2,1)的直线l与圆O交于P,Q两点,当△OPQ的面积最大时,直线l的方程为( D )
A.x-y-3=0或7x-y-15=0
B.x+y+3=0或7x+y-15=0
C.x+y-3=0或7x-y+15=0
D.x+y-3=0或7x+y-15=0
解析:当直线l的斜率不存在时,l的方程为x=2,则P,Q的坐标为(2,),(2,-),所以S△OPQ=×2×2=2.当直线l的斜率存在时,设l的方程为y-1=k(x-2),则圆心到直线PQ的距离d=,由平面几何知识得|PQ|=2,S△OPQ
=·|PQ|·d=·2·d=≤
=,当且仅当9-d2=d2,即d2=时,S△OPQ取得最大值.因为2<,所以S△OPQ的最大值为,此时=,解得k=-1或k=-7,此时直线l的方程为x+y-3=0或7x+y-15=0.故选D.
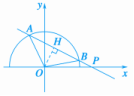
13.(2019·南宁、柳州联考)过点(,0)作直线l与曲线y=相交于A,B两点,O为坐标原点,当△AOB的面积取最大值时,直线l的斜率等于-.
解析:令P(,0),如图,易知|OA|=|OB|=1,所以S△AOB=|OA|·|OB|·sin∠AOB=sin∠AOB≤,当∠AOB=90°时,△AOB的面积取得最大值,此时过点O作OH⊥AB于点H,则|OH|=,于是sin∠OPH===,易知∠OPH为锐角,所以∠OPH=30°,则直线AB的倾斜角为150°,故直线AB的斜率为tan150°=-.
14.如图,在等腰△ABC中,已知|AB|=|AC|,B(-1,0),AC边的中点为D(2,0),则点C的轨迹所包围的图形的面积为4π.
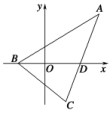
解析:解法1:设C坐标为(x,y),则A坐标为(4-x,-y),∵|AB|=|AC|,
∴=,整理得(x-1)2+y2=4(y≠0),所以C的轨迹包围的图形面积为4π.
解法2:由已知|AB|=2|AD|,设点A(x,y),则(x+1)2+y2=4[(x-2)2+y2],所以点A的轨迹方程为(x-3)2+y2=4(y≠0),设C(x′,y′),由AC边的中点为D(2,0)知A(4-x′,-y′),所以C的轨迹方程为(4-x′-3)2+(-y′)2=4,即(x-1)2+y2=4(y≠0),所以点C的轨迹所包围的图形面积为4π.
15.(2019·福州高三考试)抛物线C:y=2x2-4x+a与两坐标轴有三个交点,其中与y轴的交点为P.
(1)若点Q(x,y)(1<x<4)在C上,求直线PQ斜率的取值范围;
(2)证明:经过这三个交点的圆E过定点.
解:(1)由题意得P(0,a)(a≠0),Q(x,2x2-4x+a)(1<x<4),
故kPQ==2x-4,
因为1<x<4,所以-2<kPQ<4,
所以直线PQ的斜率的取值范围为(-2,4).
(2)证明:P(0,a)(a≠0).
令2x2-4x+a=0,
则Δ=16-8a>0,a<2,且a≠0,
解得x=1±,
故抛物线C与x轴交于A(1-,0),B(1+,0)两点.
故可设圆E的圆心为M(1,t),
由|MP|2=|MA|2,
得12+(t-a)2=()2+t2,
解得t=+,
则圆E的半径
r=|MP|=.
所以圆E的方程为(x-1)2+(y--)2=1+(-)2,
所以圆E的一般方程为
x2+y2-2x-(a+)y+=0,
即x2+y2-2x-y+a(-y)=0.
由
得或
故圆E过定点(0,),(2,).
2024年新高考数学一轮复习题型归类与强化测试专题50圆的方程(Word版附解析): 这是一份2024年新高考数学一轮复习题型归类与强化测试专题50圆的方程(Word版附解析),共34页。试卷主要包含了【知识梳理】,【题型归类】,【培优训练】,【强化测试】等内容,欢迎下载使用。
高考数学一轮复习课时作业:1 集合 Word版含解析: 这是一份高考数学一轮复习课时作业:1 集合 Word版含解析,共7页。试卷主要包含了选择题,填空题等内容,欢迎下载使用。
(新高考)高考数学一轮复习课时练习9.3《圆的方程》(含解析): 这是一份(新高考)高考数学一轮复习课时练习9.3《圆的方程》(含解析),共14页。试卷主要包含了圆的定义与方程,已知圆经过点A和B等内容,欢迎下载使用。












