高考数学一轮复习课时作业：53 双曲线 Word版含解析

这是一份高考数学一轮复习课时作业：53 双曲线 Word版含解析，共10页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
课时作业53　双曲线一、选择题1．(2018·浙江卷)双曲线－y2＝1的焦点坐标是(　B　)A．(－，0)，(，0)    B．(－2,0)，(2,0)C．(0，－)，(0，)    D．(0，－2)，(0,2)解析：由题可知双曲线的焦点在x轴上，因为c2＝a2＋b2＝3＋1＝4，所以c＝2，故焦点坐标为(－2,0)，(2,0)．故选B.2．已知双曲线C的渐近线方程为y＝±2x，且经过点(2,2)，则C的方程为(　A　)A.－＝1   B.－＝1C.－＝1   D.－＝1解析：由题意，设双曲线C的方程为－x2＝λ(λ≠0)，因为双曲线C过点(2,2)，则－22＝λ，解得λ＝－3，所以双曲线C的方程为－x2＝－3，即－＝1.3．设双曲线－＝1(a>0，b>0)的右焦点是F，左、右顶点分别为A1，A2，过F作A1A2的垂线与双曲线交于B，C两点．若A1B⊥A2C，则该双曲线的渐近线的斜率为(　C　)A．±    B．±C．±1    D．±解析：由题设易知A1(－a,0)，A2(a,0)，B，C.∵A1B⊥A2C，∴·＝－1，整理得a＝b.∵渐近线方程为y＝±x，即y＝±x，∴渐近线的斜率为±1.4．设双曲线－＝1的左、右焦点分别为F1，F2，过点F1的直线l交双曲线左支于A，B两点，则|BF2|＋|AF2|的最小值为(　B　)A.    B．11C．12    D．16解析：由题意，得所以|BF2|＋|AF2|＝8＋|AF1|＋|BF1|＝8＋|AB|，显然，当AB垂直于x轴时其长度最短，|AB|min＝2·＝3，故(|BF2|＋|AF2|)min＝11.5．(2019·河南新乡模拟)已知双曲线C：－＝1(a>0，b>0)的右焦点为F，点B是虚轴的一个端点，线段BF与双曲线C的右支交于点A，若＝2，且||＝4，则双曲线C的方程为(　D　)A.－＝1   B.－＝1C.－＝1   D.－＝1解析：不妨设B(0，b)，由＝2，F(c,0)，可得A，代入双曲线C的方程可得×－＝1，即·＝，∴＝，①又||＝＝4，c2＝a2＋b2，∴a2＋2b2＝16，②由①②可得，a2＝4，b2＝6，∴双曲线C的方程为－＝1，故选D.6．(2019·山东泰安联考)已知双曲线C1：－＝1(a>0，b>0)，圆C2：x2＋y2－2ax＋a2＝0，若双曲线C1的一条渐近线与圆C2有两个不同的交点，则双曲线C1的离心率的范围是(　A　)A.   B.C．(1,2)    D．(2，＋∞)解析：由双曲线方程可得其渐近线方程为y＝±x，即bx±ay＝0，圆C2：x2＋y2－2ax＋a2＝0可化为(x－a)2＋y2＝a2，圆心C2的坐标为(a,0)，半径r＝a，由双曲线C1的一条渐近线与圆C2有两个不同的交点，得<a，即c>2b，即c2>4b2，又知b2＝c2－a2，所以c2>4(c2－a2)，即c2<a2，所以e＝<，又知e>1，所以双曲线C1的离心率的取值范围为，故选A.二、填空题7．实轴长为2，虚轴长为4的双曲线的标准方程为x2－＝1或y2－＝1.解析：2a＝2,2b＝4.当焦点在x轴时，双曲线的标准方程为x2－＝1；当焦点在y轴时，双曲线的标准方程为y2－＝1.8．(2019·河南安阳二模)已知焦点在x轴上的双曲线＋＝1，它的焦点到渐近线的距离的取值范围是(0,2)．解析：对于焦点在x轴上的双曲线－＝1(a>0，b>0)，它的焦点(c,0)到渐近线bx－ay＝0的距离为＝b.本题中，双曲线＋＝1即－＝1，其焦点在x轴上，则解得4<m<8，则焦点到渐近线的距离d＝∈(0,2)．9．设F1，F2分别是双曲线x2－＝1的左、右焦点，A是双曲线上在第一象限内的点，若|AF2|＝2且∠F1AF2＝45°，延长AF2交双曲线右支于点B，则△F1AB的面积等于4.解析：由题意可得|AF2|＝2，|AF1|＝4，则|AB|＝|AF2|＋|BF2|＝2＋|BF2|＝|BF1|.又∠F1AF2＝45°，所以△ABF1是以AF1为斜边的等腰直角三角形，则|AB|＝|BF1|＝2，所以其面积为×2×2＝4.10．(2019·福建六校联考)已知双曲线C：－＝1(a>0，b>0)的右焦点为F，左顶点为A，以F为圆心，FA为半径的圆交C的右支于P，Q两点，△APQ的一个内角为60°，则双曲线C的离心率为.解析：设左焦点为F1，由于双曲线和圆都关于x轴对称，又△APQ的一个内角为60°，所以△APQ为正三角形，则∠PFx＝60°，所以PF＝AF＝a＋c，∴PF1＝3a＋c，在△PFF1中，由余弦定理可得PF＝PF2＋FF－2PF·FF1cos120°.故3c2－ac－4a2＝0，整理得3e2－e－4＝0，解得e＝.三、解答题11．已知双曲线C：－＝1(a>0，b>0)的离心率为，点(，0)是双曲线的一个顶点．(1)求双曲线的方程；(2)经过双曲线右焦点F2作倾斜角为30°的直线，直线与双曲线交于不同的两点A，B，求|AB|.解：(1)∵双曲线C：－＝1(a>0，b>0)的离心率为，点(，0)是双曲线的一个顶点，∴解得c＝3，b＝，∴双曲线的方程为－＝1.(2)双曲线－＝1的右焦点为F2(3,0)，∴经过双曲线右焦点F2且倾斜角为30°的直线的方程为y＝(x－3)．联立得5x2＋6x－27＝0.设A(x1，y1)，B(x2，y2)，则x1＋x2＝－，x1x2＝－.所以|AB|＝×＝.12．(2019·湛江模拟)已知双曲线－＝1(a>0，b>0)的右焦点为F(c,0)．(1)若双曲线的一条渐近线方程为y＝x且c＝2，求双曲线的方程；(2)以原点O为圆心，c为半径作圆，该圆与双曲线在第一象限的交点为A，过A作圆的切线，斜率为－，求双曲线的离心率．解：(1)因为双曲线的渐近线方程为y＝±x，所以a＝b.所以c2＝a2＋b2＝2a2＝4，所以a2＝b2＝2，所以双曲线方程为－＝1.(2)设点A的坐标为(x0，y0)，所以直线AO的斜率满足·(－)＝－1，所以x0＝y0，①依题意，圆的方程为x2＋y2＝c2，将①代入圆的方程得3y＋y＝c2，即y0＝c，所以x0＝c，所以点A的坐标为，代入双曲线方程得－＝1，即b2c2－a2c2＝a2b2，②又因为a2＋b2＝c2，所以将b2＝c2－a2代入②式，整理得c4－2a2c2＋a4＝0，所以34－82＋4＝0，所以(3e2－2)(e2－2)＝0，因为e>1，所以e＝，所以双曲线的离心率为.13．(2019·河南洛阳联考)设F1，F2分别为双曲线－＝1的左、右焦点，过F1引圆x2＋y2＝9的切线F1P交双曲线的右支于点P，T为切点，M为线段F1P的中点，O为坐标原点，则|MO|－|MT|等于(　D　)A．4    B．3C．2    D．1解析：连接PF2，OT，则有|MO|＝|PF2|＝(|PF1|－2a)＝(|PF1|－6)＝|PF1|－3，|MT|＝·|PF1|－|F1T|＝|PF1|－＝|PF1|－4，于是有|MO|－|MT|＝－＝1，故选D.14．(2019·河南适应性测试)已知F1，F2分别是双曲线－＝1(a>0，b>0)的左、右焦点，P是双曲线上一点，若|PF1|＋|PF2|＝6a，且△PF1F2的最小内角为，则双曲线的渐近线方程为(　D　)A．y＝±2x    B．y＝±xC．y＝±x    D．y＝±x解析：不妨设P为双曲线右支上一点，则|PF1|>|PF2|，由双曲线的定义得|PF1|－|PF2|＝2a，又|PF1|＋|PF2|＝6a，所以|PF1|＝4a，|PF2|＝2a.又因为所以∠PF1F2为最小内角，故∠PF1F2＝.由余弦定理，可得＝，即(a－c)2＝0，所以c＝a，则b＝a，所以双曲线的渐近线方程为y＝±x，故选D.15．(2019·河北衡水中学二模)已知双曲线C：x2－＝1(b>0)的左、右焦点分别为F1、F2，点P是双曲线C上的任意一点，过点P作双曲线C的两条渐近线的平行线，分别与两条渐近线交于A，B两点，若四边形PAOB(O为坐标原点)的面积为，且·>0，则点P的横坐标的取值范围为(　A　)A.∪B.C.∪D.解析：由题易知四边形PAOB为平行四边形，且不妨设双曲线C的渐近线OA：bx－y＝0，OB：bx＋y＝0.设点P(m，n)，则直线PB的方程为y－n＝b(x－m)，且点P到渐近线OB的距离为d＝.由解得∴B，∴|OB|＝＝|bm－n|，∴S▱PAOB＝|OB|·d＝.又∵m2－＝1，∴b2m2－n2＝b2，∴S▱PAOB＝b.又S▱PAOB＝，∴b＝2.∴双曲线C的方程为x2－＝1，∴c＝3，∴F1(－3,0)，F2(3,0)，∴·＝(－3－m)(3－m)＋n2>0，即m2－9＋n2>0，又∵m2－＝1，∴m2－9＋8(m2－1)>0，解得m>或m<－，∴点P的横坐标的取值范围为－∞，－∪，故选A.16．(2019·河南天一大联考)已知F1(－c,0)、F2(c,0)为双曲线C：－＝1(a>0，b>0)的左、右焦点，过双曲线C的左焦点的直线与双曲线C的左支交于Q，R两点(Q在第二象限内)，连接RO(O为坐标原点)并延长交C的右支于点P，若|F1P|＝|F1Q|，∠F1PF2＝π，则双曲线C的离心率为.解析：如图，设|PF1|＝x，则|PF2|＝x－2a，作Q关于原点对称的点S，连接PS，RS，SF1.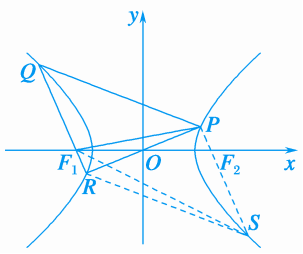因为双曲线关于原点中心对称，所以|PO|＝|OR|，S在双曲线上，所以四边形PSRQ是平行四边形，根据对称性知，F2在线段PS上，|F2S|＝|QF1|＝x，则∠F1PS＝，根据双曲线的定义，有|F1S|＝x＋2a，所以在△PF1S中，由余弦定理得(x＋2a)2＝x2＋(2x－2a)2－2·x(2x－2a)·，解得x＝a，所以|PF2|＝a，所以在△PF1F2中，由余弦定理得4c2＝2＋2－2××a×a，整理可得e＝＝.