高考数学一轮复习检测：第8章第6节 抛物线 含解析

这是一份高考数学一轮复习检测：第8章第6节 抛物线 含解析，共9页。试卷主要包含了已知点A在抛物线C，已知抛物线C，设抛物线C，抛物线C等内容，欢迎下载使用。
限时规范训练(限时练·夯基练·提能练)A级　基础夯实练1．已知点A(－2，3)在抛物线C：y2＝2px(p＞0)的准线上，记C的焦点为F，则直线AF的斜率为(　　)A．－　　　　　　　　　 B．－1C．－  D．－解析：选C.由已知，得准线方程为x＝－2，所以F的坐标为(2，0)．又A(－2，3)，所以直线AF的斜率为k＝＝－.2．若点A，B在抛物线y2＝2px(p＞0)上，O是坐标原点，若正三角形OAB的面积为4，则该抛物线方程是(　　)A．y2＝x  B．y2＝xC．y2＝2x  D．y2＝x解析：选A.根据抛物线的对称性，AB⊥x轴，由于正三角形的面积是4，故AB2＝4，故AB＝4，正三角形的高为2，故可以设点A的坐标为(2，2)代入抛物线方程得4＝4p，解得p＝，故所求的抛物线方程为y2＝x.故选A.3．(2018·皖北协作区联考)已知抛物线C：x2＝2py(p＞0)，若直线y＝2x被抛物线所截弦长为4，则抛物线C的方程为(　　)A．x2＝8y  B．x2＝4yC．x2＝2y  D．x2＝y解析：选C.由得或即两交点坐标为(0，0)和(4p，8p)，则＝4，得p＝1(舍去负值)，故抛物线C的方程为x2＝2y.4．(2018·湖南省五市十校联考)已知抛物线y2＝2x上一点A到焦点F的距离与其到对称轴的距离之比为5∶4，且|AF|＞2，则点A到原点的距离为(　　)A.  B．2C．4  D．8解析：选B.令点A到点F的距离为5a，点A到x轴的距离为4a，则点A的坐标为，代入y2＝2x中，解得a＝或a＝(舍)，此时A(2，2)，故点A到原点的距离为2.5．(2018·太原模拟)已知抛物线C：y2＝8x的焦点为F，准线为l，P是l上一点，Q是直线PF与C的一个交点．若＝4，则|QF|等于(　　)A.  B．C．3  D．2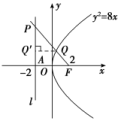解析：选C.因为＝4，所以||＝4||，所以＝.如图，过Q作QQ′⊥l，垂足为Q′，设l与x轴的交点为A，则|AF|＝4，所以＝＝，所以|QQ′|＝3，根据抛物线定义可知|QQ′|＝|QF|＝3.6．(2018·江西协作体联考)设抛物线C：y2＝2px(p＞0)的焦点为F，点M在C上，|MF|＝5.若以MF为直径的圆过点(0，2)，则C的方程为(　　)A．y2＝4x或y2＝8x  B．y2＝2x或y2＝8xC．y2＝4x或y2＝16x  D．y2＝2x或y2＝16x解析：选C.由已知得抛物线的焦点F，设点A(0，2)，抛物线上点M(x0，y0)，则＝，＝.由已知得，·＝0，即y－8y0＋16＝0，因而y0＝4，M.由|MF|＝5得，＝5，又p＞0，解得p＝2或p＝8，即抛物线方程为y2＝4x或y2＝16x.7．(2018·云南大理州模拟)在直角坐标系xOy中，有一定点M(－1，2)，若线段OM的垂直平分线过抛物线x2＝2py(p＞0)的焦点，则该抛物线的准线方程是________．解析：依题意可得线段OM的垂直平分线的方程为2x－4y＋5＝0，把焦点坐标代入可求得p＝，所以准线方程为y＝－.答案：y＝－8．(2018·河北六校模拟)抛物线C：y2＝2px(p＞0)的焦点为F，点O是坐标原点，过点O，F的圆与抛物线C的准线相切，且该圆的面积为36π，则抛物线的方程为________．解析：设满足题意的圆的圆心为M.根据题意可知圆心M在抛物线上，又因为圆的面积为36π，所以圆的半径为6，则|MF|＝xM＋＝6，即xM＝6－，又由题意可知xM＝，所以＝6－，解得p＝8.所以抛物线方程为y2＝16x.答案：y2＝16x9．设P是抛物线y2＝4x上的一个动点，则点P到点A(－1，1)的距离与点P到直线x＝－1的距离之和的最小值为________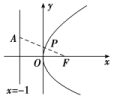． 解析：如图，易知抛物线的焦点为F(1，0)，准线方程是x＝－1，由抛物线的定义知，点P到直线x＝－1的距离等于点P到F的距离．于是问题转化为在抛物线上求一点P，使点P到点A(－1，1)的距离与点P到F(1，0)的距离之和最小，连接AF交抛物线于点P，此时最小值为|AF|＝＝.答案：10．(2018·湖北武汉调研测试)已知抛物线C：x2＝2py(p＞0)和定点M(0，1)，设过点M的动直线交抛物线C于A，B两点，抛物线C在A，B处的切线的交点为N.(1)若N在以AB为直径的圆上，求p的值；(2)若△ABN的面积的最小值为4，求抛物线C的方程．解：由题意知，直线AB的斜率一定存在，∴设直线AB：y＝kx＋1，A(x1，y1)，B(x2，y2)，将直线AB的方程代入抛物线C的方程得x2－2pkx－2p＝0，则x1＋x2＝2pk，x1x2＝－2p.①(1)由x2＝2py得y′＝，则A，B处的切线斜率的乘积为＝－，∵点N在以AB为直径的圆上，∴AN⊥BN，∴－＝－1，∴p＝2.(2)易得直线AN：y－y1＝(x－x1)，直线BN：y－y2＝(x－x2)，联立，得结合①式，解得即N(pk，－1)．|AB|＝|x2－x1|＝＝，点N到直线AB的距离d＝＝，则S△ABN＝·|AB|·d＝≥2，当k＝0时，取等号，∵△ABN的面积的最小值为4，∴2＝4，∴p＝2，故抛物线C的方程为x2＝4y.B级　能力提升练11．(2018·河北邯郸质检)已知抛物线y2＝2px(p＞0)过点A，其准线与x轴交于点B，直线AB与抛物线的另一个交点为M，若＝λ，则实数λ为(　　)A.  B．C．2  D．3解析：选C.把点A代入抛物线的方程得2＝2p×，解得p＝2，所以抛物线的方程为y2＝4x，则B(－1，0)，设M，则＝，＝(－1－，－yM)，由＝λ，得解得λ＝2或λ＝1(舍去)，故选C.12．(2018·河南郑州模拟)已知抛物线y2＝8x，点Q是圆C：x2＋y2＋2x－8y＋13＝0上任意一点，记抛物线上任意一点P到直线x＝－2的距离为d，则|PQ|＋d的最小值为(　　)A．5  B．4C．3  D．2 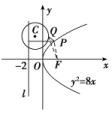解析：选C.如图，由题意知抛物线y2＝8x的焦点为F(2，0)，连接PF，FQ，则d＝|PF|，将圆C的方程化为(x＋1)2＋(y－4)2＝4，圆心为C(－1，4)，半径为2，则|PQ|＋d＝|PQ|＋|PF|，又|PQ|＋|PF|≥|FQ|(当且仅当F，P，Q三点共线时取得等号)．所以当F，Q，C三点共线时取得最小值，且为|CF|－|CQ|＝－2＝3，故选C.13．(2018·广东五校联考)已知过抛物线C：y2＝8x的焦点F的直线l交抛物线于P，Q两点，若R为线段PQ的中点，连接OR并延长交抛物线C于点S，则的取值范围是(　　)A．(0，2)  B．[2，＋∞)C．(0，2]  D．(2，＋∞)解析：选D.由题意知，抛物线y2＝8x的焦点F的坐标为(2，0)，直线l的斜率存在且不为0，设直线l的方程为y＝k(x－2)．由消去y整理得k2x2－4(k2＋2)x＋4k2＝0，设P(x1，y1)，Q(x2，y2)，R(x0，y0)，S(x3，y3)，则x1＋x2＝，故x0＝＝，y0＝k(x0－2)＝，所以kOS＝＝，直线OS的方程为y＝x，代入抛物线方程，解得x3＝，由条件知k2＞0.所以＝＝k2＋2＞2.选D.14．(2018·河南洛阳统一考试)已知抛物线C：x2＝4y的焦点为F，直线AB与抛物线C相交于A，B两点，若2＋－3＝0，则弦AB中点到抛物线C的准线的距离为________．解析：依题意得，抛物线的焦点为F(0，1)，准线方程是y＝－1，因为2(－)＋(－)＝0，即2＋＝0，所以F，A，B三点共线．设直线AB：y＝kx＋1(k≠0)，A(x1，y1)，B(x2，y2)，则由得x2＝4(kx＋1)，即x2－4kx－4＝0，x1x2＝－4　①；又2＋＝0，因此2x1＋x2＝0　②.由①②解得x＝2，弦AB的中点到抛物线C的准线的距离为[(y1＋1)＋(y2＋1)]＝(y1＋y2)＋1＝(x＋x)＋1＝＋1＝.答案：15．已知F是抛物线y2＝4x的焦点，点A，B在该抛物线上且位于x轴的两侧，·＝－4(其中O为坐标原点)，则△ABO面积的最小值是________．解析：不妨设A(x1，y1)，B(x2，y2)，y1＞0，由·＝－4，即x1x2＋y1y2＝－4得yy＋y1y2＝－4，得y1y2＝－8.所以S△ABO＝|x1y2－x2y1|＝|y1－y2|≥4，当y1＝2，y2＝－2时取等号，故△ABO面积的最小值为4.答案：4C级　素养加强练16．已知抛物线C：y2＝2px过点P(1，1)．过点作直线l与抛物线C交于不同的两点M，N，过点M作x轴的垂线分别与直线OP，ON交于点A，B，其中O为原点．(1)求抛物线C的方程，并求其焦点坐标和准线方程；(2)求证：A为线段BM的中点．解：(1)把P(1，1)代入y2＝2px得p＝，所以抛物线C：y2＝x，所以焦点坐标为，准线：x＝－.(2)证明：设l：y＝kx＋，M(x1，y1)，N(x2，y2)，OP：y＝x，ON：y＝x，由题知A(x1，x1)，B，由消去y得k2x2＋(k－1)x＋＝0，所以x1＋x2＝，x1·x2＝.所以y1＋＝kx1＋＋＝2kx1＋，由x1＋x2＝，x1x2＝，上式＝2kx1＋＝2kx1＋(1－k)·2x1＝2x1，所以A为线段BM的中点．