第1章二次函数章末复习教案（湘教版九下）

章末复习

【知识与技能】

掌握本章重要知识,能灵活运用二次函数的图象与性质解决实际问题.

【过程与方法】

通过梳理本章知识,回顾解决问题中所涉及的数形结合思想,转化化归思想的过程,加深对本章知识的理解.

【情感态度】

在运用本章知识解决具体问题过程中,进一步体会数学与生活的密切联系,激发学习兴趣.

【教学重点】

回顾本章知识点,构建知识体系.

【教学难点】

利用二次函数的相关知识解决具体问题.

一、知识框图，整体把握

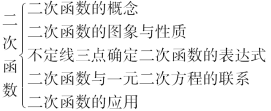
【教学说明】引导学生回顾本章知识点,展示本章知识结构框图,使学生系统了解本章知识及它们之间的关系,教学时,边回顾边建立结构框图.

二、释疑解惑，加深理解

1.由于y=ax2+bx+c配方后可得y= ,所以y=ax2+bx+c的图象总可由y=ax2平移得到.

2.对于现实生活中的许多问题，可以通过建立二次函数模型来解决.

3.利用二次函数解法实际问题时,自变量的取值范围要结合具体问题来确定.

三、典例精析，复习新知

例1  下列函数中,是二次函数的是(     )

A.y=8x2+1    B.y=x2+    C.y=(x-2)(x+2)-x2    D.y=ax2

【解析】选A.选项A符合二次函数的一般形式，是二次函数，正确；选项B不是整式形式，错误；选项C不含二次项，错误；选项D，二次项系数a=0时，不是二次函数，错误.

例2  抛物线y=-(x-1)2是由抛物线y=-(x+3)2向         平移         个单位得到的；平移后的抛物线对称轴是         ，顶点坐标是         ，当x=         时，函数y有最         值，其值是         .

【解析】本题因为a=-1＜0，所以抛物线开口向下，函数有最大值；掌握“左加右减”的平移规律时，关键是把握平移方向.

答案:右   4   直线x=1   (1,0)   1   大   0

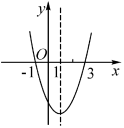
例3  如图为二次函数y=ax2+bx+c的图象，

在下列说法中：①ac＜0;②方程ax2+bx+c=0

的根是x1=-1,x2=3;③a+b+c＞0；④当x＞1时，

y随着x的增大而增大.正确的说法有             .(请写出所有正确说法的序号)

【解析】∵抛物线开口向上,即a＞0;与y轴的交点在x轴下方，即c＜0,∴ac＜0,①正确；

由函数图象与x轴的交点坐标（-1，0），（3，0），可得方程ax2+bx+c=0的根为x1=-1,x2=3,②正确；

由函数图象与x=1的交点位于x轴下方，即a+b+c＜0，③错误；

由函数图象可得抛物线的对称轴为x=1,当x＞1时，y随着x的增大而增大，故正确的说法有①②④.

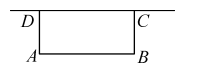
例4  如图，利用一面墙（墙长为15m)和30m长的篱笆来围矩形场地，若设垂直墙的一边长为x(m)，围成的矩形场地的面积为y(m2).

(1)求y与x之间的函数解析式，并写出自变量x的

取值范围;

(2)怎样围成一个面积为112m2的矩形场地？

（3）若要围成一个面积最大的矩形场地，则矩形场地的长和宽各应是多少？

【解析】

 (1)∵AD=BC=x,∴AB=30-2x,由题意得y=x(30-2x)=-2x2+30x(7.5≤x＜15);

(2)当y=112时，-2x2+30x=112,解得:x1=7,x2=8,

当x=7时，AD=BC=7m,AB=30-2×7=16m(大于围墙的长度，舍去）.

当x=8时，AD=BC=8cm,AB=30-2×8=14m(符合题意)

∴当垂直于墙面的边长为8m时，可以围成面积为112m2的矩形场地.

(3)y=-2x2+30x=-2（x-）2+

∴当x=m时，围成的面积最大，此时矩形的宽为m,长为15m.

四、运用新知，深化理解

1.(江苏扬州中考）将抛物线y=x2+1先向左平移2个单位，再向下平移3个单位，那么所得抛物线的函数解析式是（      ）

A.y=(x+2)2+3   B.y=(x+2)2-3   C.y=(x-2)2+3   D.y=(x-2)2-3

2.已知二次函数y=ax2+bx+c中，其函数y与自变量x之间的部分对应值如下表所示：

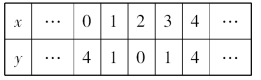
点A（x1,y1),B(x2,y2)在函数的图象上，则当1＜x1＜2,3＜x2＜4时，y1与y2的大小关系正确的是（      ）

A.y1＞y2    B.y1＜y2    C.y1≥y2    D.y1≤y2

3.（湖北咸宁中考）对于二次函数y=x2-2mx-3，有下列说法：

①它的图象与x轴有两个公共点；

②如果当x≤1时，y随x的增大而减小，则m=1;

③如果将它的图象向左平移3个单位后过原点，则m=-1;

④如果当x=4时的函数值与x=2008时的函数值相等，则当x=2012时的函数值为-3.

其中正确的说法是              .(把你认为正确说法的序号都填上)

4.如图所示，二次函数y=-x2+2x+m的图象与x轴的一个交点为A（3，0），另一个交点为B，且与y轴交于点C.

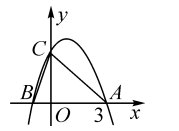（1）求m的值；

（2）求点B的坐标；

（3）该二次函数图象上有一点D（x,y)（其

中x＞0,y＞0),使S△ABD=S,求点D的坐标.

5.某商场销售某种品牌的纯牛奶,已知进价为每箱40元,生产厂家要求每箱售价在40元~70元之间.经市场调查发现;若以每箱50元销售,平均每天可售出90箱,价格每降低1元,平均每天多销售3箱;价格每升高1元,平均每天少销售3箱.

(1)写出售价x(元）与平均每天所得利润W(元）之间的函数关系式；

（2）每箱定价多少元时，才能使平均每天的利润最大？最大利润是多少？

【答案】1.B   2.B   3.①④  

4.(1)m=3   (2)y=-x2+2x+3   令y=0解得x=3或-1，∴B（-1，0）

（3）∵S△ABD=S△ABC，点D在第一象限.∴点C,D关于二次函数对称轴对称.

∵对称轴x=1,C(0,3),∴D(2,3)

5.解：（1）设销售量为y箱，则y=240-3x,

所以W=(x-40)y=(x-40)(240-3x)=-3(x-60)2+1200(40≤x≤70).

(2)当x=60时，W最大=1200.∴每箱定价为60元时，才能使平均每天的利润最大，最大利润是1200元.

五、师生互动，课堂小结

你能完整地回顾本章所学的二次函数的有关知识吗?你能用二次函数知识解决实际问题吗?你还有哪些疑问?

1.教材P37第3~6题.

2.完成同步练习册中本课时的练习.

本节通过学习归纳本章内容,建立二次函数模型,掌握二次函数性质,并利用二次函数性质去解决实际问题,查漏补缺,使学生对本章知识有通盘了解和掌握.