
【单元检测】北师大版数学八年级上册--第一章 《勾股定理》单元测试卷 (含答案)
展开第一章 《勾股定理》单元测试卷
一、选择题:本题共12个小题,每小题3分,共36分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.为了求出湖两岸的A、B两点之间的距离,一个观测者在点C设桩,使三角形ABC恰好为直角三角形.如图,通过测量,得到AC长160 m,BC长128 m,则从点A穿过湖到点B的距离是( )
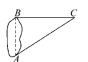
A.48 m B.90 m C.96 m D.69 m
2.五根小木棒,其长度分别为7,15,20,24,25,现将它们摆成两个直角三角形,其中正确的是( )
A.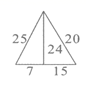 B.
B.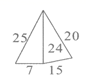 C.
C.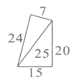 D.
D.
3.《九章算术》是我国古代的数学名著,其中“勾股”章有一题,大意是说:已知矩形门的高比宽多![]() 尺,门的对角线长
尺,门的对角线长![]() 尺,那么门的高和宽各是多少?如果设门的宽为
尺,那么门的高和宽各是多少?如果设门的宽为![]() 尺,根据题意可列方程( )
尺,根据题意可列方程( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
4.已知ΔABC的三边分别长为a,b,c,且满足![]() +|b-15|+
+|b-15|+![]() -16c+64=0,则ΔABC是( )
-16c+64=0,则ΔABC是( )
A.以a为斜边的直角三角形 B.以b为斜边的直角三角形
C.以c为斜边的直角三角形 D.不是直角三角形
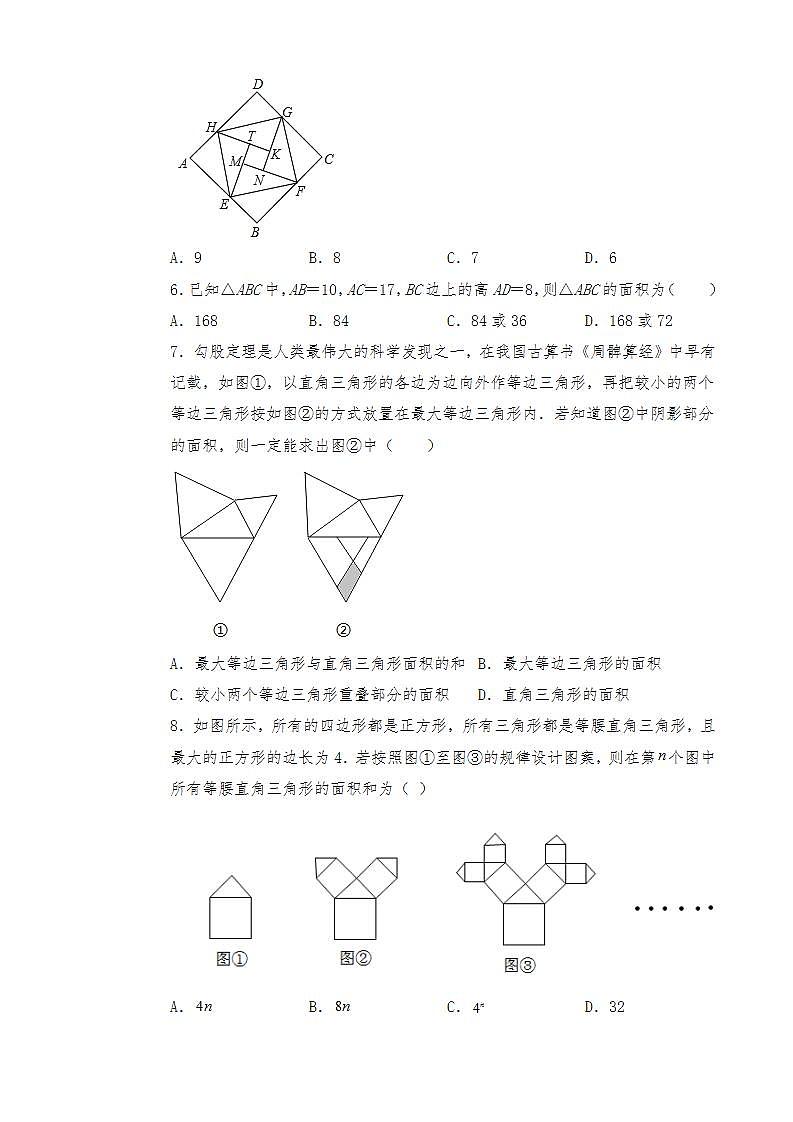
5.我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”,它是用八个全等的直角三角形拼接而成,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3.若![]() ,则S2的值是( )
,则S2的值是( )
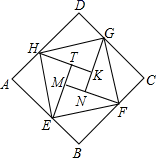
A.9 B.8 C.7 D.6
6.已知△ABC中,AB=10,AC=17,BC边上的高AD=8,则△ABC的面积为( )
A.168 B.84 C.84或36 D.168或72
7.勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载,如图①,以直角三角形的各边为边向外作等边三角形,再把较小的两个等边三角形按如图②的方式放置在最大等边三角形内.若知道图②中阴影部分的面积,则一定能求出图②中( )
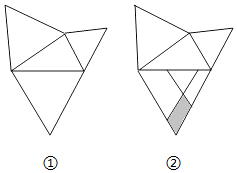
A.最大等边三角形与直角三角形面积的和 B.最大等边三角形的面积
C.较小两个等边三角形重叠部分的面积 D.直角三角形的面积
8.如图所示,所有的四边形都是正方形,所有三角形都是等腰直角三角形,且最大的正方形的边长为4.若按照图①至图③的规律设计图案,则在第![]() 个图中所有等腰直角三角形的面积和为( )
个图中所有等腰直角三角形的面积和为( )
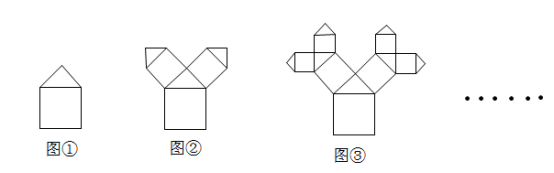
A.![]() B.
B.![]() C.
C.![]() D.32
D.32
9.如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线D′处.若AB=3,AD=4,则ED的长为
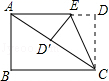
A.![]() B.3 C.1 D.
B.3 C.1 D.![]()
10.勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图![]() , 以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图
, 以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图![]() 的方式放 置在最大正方形内.若图
的方式放 置在最大正方形内.若图![]() 中阴影部分的面积为
中阴影部分的面积为 ![]() ,且
,且 ![]() ,则
,则 ![]() 的长为( )
的长为( )

图1 图2
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.如图,直角三角形纸片![]() 中,
中,![]() ,
,![]() ,D为斜边
,D为斜边![]() 中点,第1次将纸片折叠,使点A与点D重合,折痕与
中点,第1次将纸片折叠,使点A与点D重合,折痕与![]() 交于点
交于点![]() ;设
;设![]() 的中点为
的中点为![]() ,第2次将纸片折叠,使点A与点
,第2次将纸片折叠,使点A与点![]() 重合,折痕与
重合,折痕与![]() 交于点
交于点![]() ;设
;设![]() 的中点为
的中点为![]() ,第3次将纸片折叠,使点A与点
,第3次将纸片折叠,使点A与点![]() 重合,折痕与
重合,折痕与![]() 交于点
交于点![]() ,则
,则![]() 的长为()
的长为()
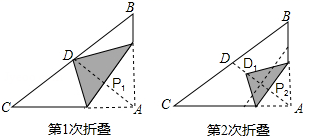
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.如图,在![]() 中,
中,![]() ,将边
,将边![]() 沿
沿![]() 折叠,使点B落在
折叠,使点B落在![]() 上的点
上的点![]() 处,再将边
处,再将边![]() 沿
沿![]() 折叠,使点A落在
折叠,使点A落在![]() 的延长线上的点
的延长线上的点![]() 处,两条折痕与斜边
处,两条折痕与斜边![]() 分别交于点N、M,则线段
分别交于点N、M,则线段![]() 的长为( )
的长为( )
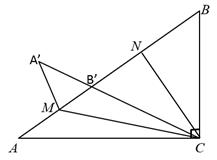
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题:本题共6个小题,每小题3分,共18分。
13.如图所示的正方形网格内,点A,B,C,D,E是网格线交点,那么![]() _____°.
_____°.

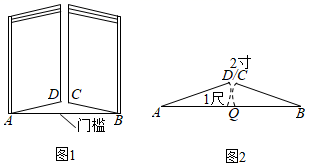
14.《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸,问门广几何?题目大意是:如图1、2(图2为图1的平面示意图),推开双门,双门间隙CD的距离为2寸,点C和点D距离门槛AB都为1尺(1尺=10寸),则AB的长是_____寸.
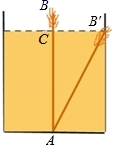
15.《九章算术》中有一道“引葭赴岸”问题:“仅有池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深,葭长各几何?”题意是:有一个池塘,其地面是边长为10尺的正方形,一棵芦苇AB生长在它的中央,高出水面部分BC为1尺.如果把芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部B恰好碰到岸边的B'(示意图如图,则水深为__尺.
16.如图,矩形![]() 中,
中,![]() ,
,![]() ,将矩形
,将矩形![]() 绕点
绕点![]() 顺时针旋转得到矩形
顺时针旋转得到矩形![]() ,边
,边![]() 与
与![]() 交于点
交于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,则
,则![]() 的长为______.
的长为______.
17.如图,Rt![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 是直线
是直线![]() 上一点,把
上一点,把![]() 沿
沿![]() 所在的直线翻折后,点
所在的直线翻折后,点![]() 落在点
落在点![]() 处,如果
处,如果![]() ,那么点
,那么点![]() 和点
和点![]() 间的距离等于______.
间的距离等于______.
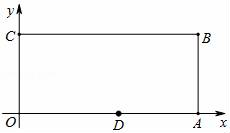
18.如图,已知在平面直角坐标系中,O为坐标原点,四边形OABC是长方形,点A、C、D的坐标分别为A(9,0)、C(0,4),D(5,0),点P从点O出发,以每秒1个单位长度的速度沿O→C→B→A运动,点P的运动时间为t秒.则当t=____秒时,△ODP是腰长为5的等腰三角形?
三、解答题(19题6分,其余每题8分,共46分)
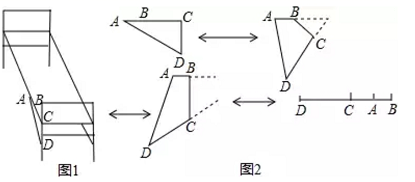
19.如图是一个可折叠的钢丝床的示意图,这是展开后支撑起来放在地面上的情况,如果折叠起来,床头部分被折到床面之上了(这里的A、B、C、D各点都是活动的).活动床头是根据三角形的稳定性和四边形的不稳定性设计而成的,其折叠过程可用如图的变换反映出来,如果已知四边形ABCD中,AB=6,CD=15,那么BC、AD取多长时,才能实现上述的折叠变化?
20.如图,在![]() 中,
中,![]() ,
,![]() 平分
平分![]() ,交
,交 ![]() 于点 D,过点 D 作
于点 D,过点 D 作 ![]() 于点 E.
于点 E.
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,求
,求![]() 的长.
的长.

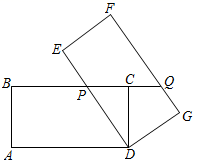
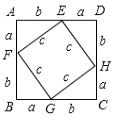
21.利用4个全等的直角三角形拼出了如图所示的图形.根据图形解决下列问题:
(1)四边形![]() ,四边形
,四边形![]() 均为________;
均为________;
(2)大正方形的面积可以表示为_______,还可以表示为________;
(3)根据(2)中大正方形面积的两种表示方法,你能得到勾股定理吗?请你说明理由.
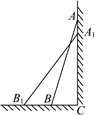
22.如图所示,A、B两块试验田相距200m,C为水源地,AC=160m,BC=120m,为了方便灌溉,现有两种方案修筑水渠.
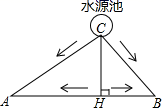
甲方案:从水源地C直接修筑两条水渠分别到A、B;
乙方案;过点C作AB的垂线,垂足为H,先从水源地C修筑一条水渠到AB所在直线上的H处,再从H分别向A、B进行修筑.
(1)请判断△ABC的形状(要求写出推理过程);
(2)两种方案中,哪一种方案所修的水渠较短?请通过计算说明.
23.如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时梯足B到墙脚C的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么点B将向外移动多少米?
(1)请你将小明对“思考题”的解答补充完整:
解:AC=![]() =2.4(米).
=2.4(米).
设点B将向外移动x米,即BB1=x米,
则B1C=(x+0.7)米,A1C=AC-AA1=2.4-0.4=2(米),
而A1B1=2.5米,在Rt△A1B1C中,由B1C2+A1C2=A1B12得方程__________________,
解方程得x1=________,x2=________.
∴点B将向外移动________米.
(2)解完“思考题”后,小明提出了如下两个问题:
(问题一)在“思考题”中,将“下滑0.4米”改为“下滑0.9米”,那么该题的答案会是0.9米吗?为什么?
(问题二)在“思考题”中,梯子的顶端从A处沿墙AC下滑的距离与点B向外移动的距离有可能相等吗?为什么?
24.阅读理解题:
(几何模型)
条件:如图1,A、B是直线l同旁的两个定点.
问题;在直线l上确定一点P,使PA+PB的值最小.
方法:作点A关于直线l的对称点A',连接A′B交l于点P,则PA+PB=A'P+PB=A'B,由“两点之间,线段最短”可知,点P即为所求的点.
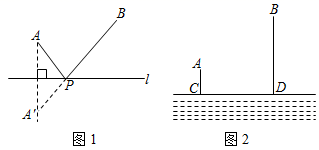
(模型应用)
如图2所示,两个村子A、B在一条河CD的同侧,A、B两村到河边的距离分别为AC=1千米,BD=3千米,CD=3千米.现要在河边CD上建造一水厂,向A、B两村送水,铺设水管的工程费用为每千米200元,请你在CD上选择水厂位置,使铺设水管的费用最省,并求出最省的铺设水管的费用W.
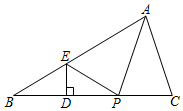
(拓展延伸)
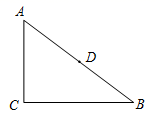
如图,△ABC中,点D在BC边上,过D作DE⊥BC交AB于点E,P为DC上的一个动点,连接PA、PE,若PA+PE最小,则点P应该满足 (唯一选项正确)
A.∠APC=∠EPD B.PA=PE
C.∠APE=90° D.∠APC=∠DEP
答案
一、选择题
C.C.A.A.C.C.C.A.A.B.D.B.
二、填空题
13.90.
14.101
15.12.
16.![]() .
.
17.2.5或10.
18.6或7或12或14.
三、解答题
19.由图1知
![]() ①
①
由图2知,AB+AD=CD+BC,即6+AD=15+BC②.
联立①②组成方程组得:
![]()
解得AD=39,BC=30.
故BC,AD分别取30和39时,才能实现上述变化.
20.(1)证明:![]() ,
,
![]() ,
,
![]() 平分
平分![]() ,
,![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
![]() ,
,
![]() (HL),
(HL),
![]() ;
;
(2)解:![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
由(1)知,![]() ,
,![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,
由勾股定理得:![]() ,
,
即![]() ,
,
解得:![]() ,
,
![]() .
.
21.(1)正方形;
(2)大正方形的面积等于边长的平方为:![]() ;大正方形的面积等于四个三角形面积加小正方形面积为:
;大正方形的面积等于四个三角形面积加小正方形面积为:![]() ;
;
(3)能.理由如下:
由(2),得![]() ,
,
即![]() ,
,
所以![]() .
.
22.解:(1)△ABC是直角三角形;
理由如下:
∴AC2+BC2=1602+1202=40000,AB2=2002=40000,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,∠ACB=90°;
(2)甲方案所修的水渠较短;
理由如下:
∵△ABC是直角三角形,
∴△ABC的面积=![]() AB•CH=
AB•CH=![]() AC•BC,
AC•BC,
∴CH=![]() (m),
(m),
∵AC+BC=160+120=280(m),CH+AH+BH=CH+AB=96+200=296(m),
∴AC+BC<CH+AH+BH,
∴甲方案所修的水渠较短.
23.解:设点B将向外移动x米,即![]() ,
,
则![]() ,
,![]()
而![]() ,在
,在![]() 中,由
中,由![]() ,
,
得方程__(x+0.7)2+22=2.5²__,
解方程得![]() =_0.8_,
=_0.8_,![]() =-2.2 (舍去),
=-2.2 (舍去),
∴点B将向外移动__0.8__米.
(2)①不会是0.9米.
若AA1=BB1=0.9,则A1C=2.4-0.9=1.5,B1C=0.7+0.9=1.6,
1.52+1.62=4.81,2.52=6.25,即A1C2+B1C2≠A1B12,
所以该题的答案不会是0.9米.
②有可能.
设梯子顶端从A处下滑x米,点B向外也移动x米,则有
(x+0.7)2+(2.4-x)2=2.52,解得x=1.7或x=0(舍去).
所以当梯子顶端从A处下滑1.7米时,点B向外也移动1.7米,
即梯子顶端从A处沿墙AC下滑的距离与点B向外移动的距离有可能相等.
24.模型应用:作点A关于CD的对称点A′,连接BA′交CD于点P,则点P即为所求的水厂位置,作A′E⊥BD交BD的延长线于点E,则四边形CA′ED为矩形,
∴DE=A′C=AC=1,A′E=CD=3,
∴BE=BD+DE=4,
由勾股定理得,A′B=![]() =
=![]() =5,
=5,
则PA+PB=A′B=5,
∴最省的铺设水管的费用W=200×5=1000(元);
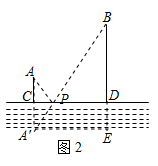
拓展延伸:延长ED至E′,连接AE′交BC于点P,则点P即为所求,连接EP,

∵点E与点E′关于BC对称,
∴∠E′PD=∠EPD,
∵∠E′PD=∠APC,
∴∠APC=∠EPD,A正确;
∵唯一选项正确,∴其余选项均错误;
故选:A.









