【单元检测】北师大版数学八年级上册--第三章《位置与坐标》单元测试卷 （含答案）

第三章《位置与坐标》单元测试卷

一、选择题：本题共12个小题，每小题3分，共36分。在每小题给出的四个选项中，只有一项是符合题目要求的。

1．下列表述，能确定具体位置的是（    ）

A．电影院2号厅3排 B．城关镇民主街

C．东经118° D．文峰塔北偏东60°，处

2．如图，学校在蕾蕾家南偏西的方向上，点表示超市所在的位置，，则超市在蕾蕾家的（ ）

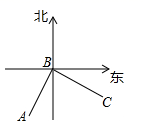
A．北偏东的方向上 B．南偏东的方向上

C．北偏东的方向上 D．南偏东的方向上

3．已知点在第四象限，且到轴的距离为，则点的坐标为（    ）

A． B． C． D．

4．某公交车上显示屏上显示的数据表示该车经过某站点时先下后上的人数．若车上原有10个人，此公交车依次经过某三个站点时，显示器上的数据如下：，则此公交车经过第二个站点后车上的人数为（    ）

A．9 B．12 C．6 D．1

5．若点A（a，3）与B（2，b）关于x轴对称（a，b）所在的象限是（    ）

A．第一象限 B．第二象限 C．第三象限 D．第四象限

6．如图是小丽与小红的微信对话记录．根据图中两个人的对话记录，若下列有一种走法能从大润发超市出发走到小丽家，则此走法为（    ）

A．向北直走900米，再向西直走100米 B．向北直走100米，再向西直走900米

C．向北直走100米，再向西直走100米 D．向北直走900米，再向东直走100米

7．如图，将1、，三个数按图中方式排列，若规定表示第排第列的数，则与表示的两个数的积是（    ）

A．1 B． C． D．

8．平面直角坐标系中，点，，经过点的直线与轴平行，如果点是直线上的一个动点，那么当线段的长度最短时，点的坐标为（    ）

A． B． C． D．

9．在平面直角坐标系中，点，点，点在坐标轴上，若的面积为12，则符合题意的点C有（    ）

A．1个 B．2个 C．3个 D．4个

10．如图所示，平面直角坐标系中，轴负半轴上有一点．点第一次向上平移1个单位至点，接着又向右平移1个单位至点，然后再向上平移1个单位至点，向右平移1个单位至点，…，照此规律平移下去，点平移至点A2021时，点的坐标是（    ）

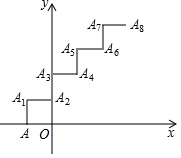
A． B． C． D．

11．数经历了从自然数到有理数，到实数，再到复数的发展过程，数学中把形如a+bi（a，b为实数）的数叫做复数，用z＝a+bi表示，任何一个复数z＝a+bi在平面直角坐标系中都可以用有序数对Z（a，b）表示，如：z＝1+2i表示为Z（1，2），则z＝2﹣i可表示为（　　）

A．Z（2，0） B．Z（2，﹣1） C．Z（2，1） D．（﹣1，2）

12．如图，小球起始时位于（3，0）处，沿所示的方向击球，小球运动的轨迹如图所示．如果小球起始时位于（1，0）处，仍按原来方向击球，小球第一次碰到球桌边时，小球的位置是（0，1），那么小球第2021次碰到球桌边时，小球的位置是（    ）

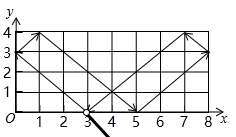
A．（3，4） B．（5，4） C．（7，0） D．（8，1）

二、填空题：本题共6个小题，每小题3分，共18分。

13．我们规定向东和向北方向为正，如向东走4米，再向北走6米，记作，则向西走5米，再向北走3米记作_________；数对表示___________．

14．在平面直角坐标系中，点到x轴的距离是______．

15．在平面直角坐标系中，若点与点关于轴对称，则______．

16．在同一平面内，甲、乙、丙三人所处的位置不同．以甲为坐标原点，乙的坐标是（2，3）；以乙为坐标原点，丙的坐标是（3，2）．若在三人所建立的平面直角坐标系中，x轴、y轴的正方向相同，则以丙为坐标原点，甲的坐标是 __________．

17．已知在平面直角坐标系中，A、B两点的坐标分别为A（1，2）、B（3，1），P，Q分别是x轴，y轴上两个动点，则四边形ABPQ的周长最小值为____．

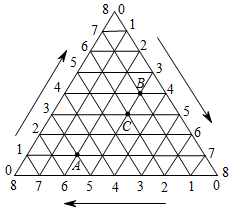
18．如图，将一等边三角形的三条边各8等分，按顺时针方向（图中箭头方向）标注各等分点的序号0、1、2、3、4、5、6、7、8，将不同边上的序号和为8的两点依次连接起来，这样就建立了“三角形”坐标系．在建立的“三角形”坐标系内，每一点的坐标用过这一点且平行（或重合）于原三角形三条边的直线与三边交点的序号来表示（水平方向开始、按顺时针方向、取与三角形外箭头方向一致的一侧序号），如点A的坐标可表示为，点B的坐标可表示为，按此方法，若点C的坐标为，则m＝__________．

三、解答题（19题6分，其余每题8分，共46分）

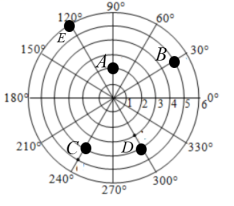
19．如图是一台雷达探测相关目标得到的结果，若记图中目标C的位置为，则其余各目标的位置分别是多少？

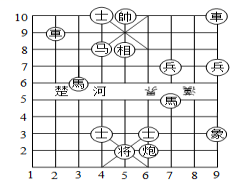
20．如图，如果“象”的位置表示为．

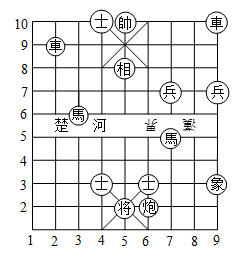
（1）用同样的方式表示“将”与“帅”的位置；

（2）“马”走“日”字对角线．在图上标出“马3进4”（即第3列的马前进到第4列）后的位置．

21．已知点P（2a＋3，a－1）．试分别根据下列条件，求出点P的坐标．

（1）点P的纵坐标比横坐标大3；        

（2）点P在过A（2，－3）点，且与x轴平行的直线上．

22．如图，已知的三个顶点的坐标分别为，，．

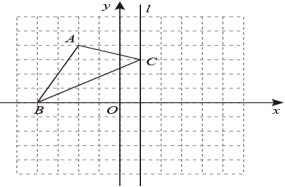
（1）画出关于x轴对称的图形，并写出点A的对称点的坐标；

（2）若直线l上的点横坐标都是1，画出关于l对称的图形，并直接写出三个顶点的坐标；

（3）若点是坐标平面内的一点，则点D关于直线l对称的点的坐标为_____（用含a、b的式子表示）．

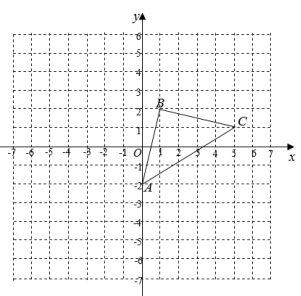
23．如图所示，在平面直角坐标系中，已知A（0，﹣2），B（1，2），C（5，1）．

（1）在平面直角坐标系中画出△ABC；

（2）若点D与点C关于y轴对称，则点D的坐标为 　 　；

（3）△ABC的面积为 　 　；

（4）已知点P为y轴上一点，若S△ACP＝5时，则点P的坐标为 　 　．

24．在平面直角坐标系中，且满足，长方形在坐标系中（如图），点为坐标系的原点．

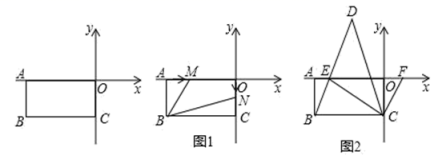
（1）求点的坐标．

（2）如图1，若点从点出发，以2个单位/秒的速度向右运动（不超过点），点从原点出发，以1个单位/秒的速度向下运动（不超过点），设、两点同时出发，在它们运动的过程中，四边形的面积是否发生变化？若不变，求其值；若变化，求变化的范围．

（3）如图2，为轴负半轴上一点，且，是轴正半轴上一动点，的平分线交的延长线于点，在点运动的过程中，请探究与的数量关系，并说明理由.

答案

一、选择题

D．D．A．C.D．B．C．C．D．C．B．B．

二、填空题

13．；向西走2米，再向南走6米.

14．2．

15．．

16．（﹣5，﹣5）．

17．5+．

18．3．

三、解答题

19．

解： 图中目标C的位置为，

目标A的位置为，目标B的位置为，

目标D的位置为，目标E的位置为，

20．

解：（1）“象”的位置表示为．

结合图形可得：象在第列，第行，

而 “将”在第列第行，所以表示为：

“帅”在第列第行，所以表示为：

（2）如图，“马3进4”后的位置在第列第行，表示为：

21．（1）∵点P（2a＋3，a－1），且点P的纵坐标比横坐标大3，

∴a-1=2a+3+3，

解得a=-7，

∴点P（-11，-8）；        

（2）∵点P在过A（2，－3）点，且与x轴平行的直线上，

∴a-1=-3，

解得a=-2，

∴点P（-1，-3）．

22．解：（1）如图所示，即为所求，

的坐标为；

（2）如图所示，即为所求，

其中的坐标为，的坐标为，的坐标为；

（3）设点D关于直线l的对称点的坐标为（x，y），

由题意可知：，，

解得：，，

∴点D关于直线l对称的点的坐标为，

故答案为：．

23．解：（1）在图中分别标记出三点，连接、、即可，如下图：

（2）点D与点C关于y轴对称，纵坐标不变，横坐标变为相反数

∵

∴

（3）由图形可知：△ABC的面积为长方形面积减去三个直角三角形的面积，

（4）设，则

，即，解得或

即或

24．

(1)∵，

∴a=−6，c=−3

∴A(−6,0),C(0,−3)

∵四边形OABC是矩形

∴AO∥BC,AB∥OC，AB=OC=3，AO=BC=6

∴B(−6,−3)

(2)四边形MBNO的面积不变.

设M、N同时出发的时间为t，

则S=S−S−S =18−×2t×3−×6×(3−t)=9.与时间无关.

∴在运动过程中面积不变，是定值9.

(3)∠CFE=2∠D.

理由如下：如图

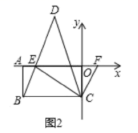
∵∠CBE=∠CEB

∴∠ECB=180°−2∠BEC

∵CDP平分∠ECF

∴∠DCE=∠DCF

∵AF∥BC

∴∠F=180°−∠DCF−∠DCE−∠BCE=180°−2∠DCE−(180°−2∠BEC)

∴∠F=2∠BEC−2∠DCE

∵∠BEC=∠D+∠DCE

∴∠F=2(∠D+∠DCE)−2∠DCE

∴∠F=2∠D