初中数学湘教版九年级下册1.2 二次函数的图像与性质第4课时教学设计

第4课时 二次函数y=a(x-h)2+k(a≠0)的图象与性质

【知识与技能】

1.会用描点法画二次函数y=a(x-h)2+k的图象.掌握y=a(x-h)2+k的图象和性质.

2.掌握y=a(x-h)2+k与y=ax2的图象的位置关系.

3.理解y=a(x-h)2+k,y=a(x-h)2,y=ax2+k及y=ax2的图象之间的平移转化.

【过程与方法】

经历探索二次函数y=a(x-h)2+k的图象的作法和性质的过程，进一步领会数形结合的思想，培养观察、分析、总结的能力.

【情感态度】

1.在小组活动中进一步体会合作与交流的重要性.

2.体验数学活动中充满着探索性,感受通过认识观察,归纳,类比可以获得数学猜想的乐趣.

【教学重点】

二次函数y=a(x-h)2+k的图象与性质.

【教学难点】

由二次函数y=a(x-h)2+k的图象的轴对称性列表、描点、连线.

一、情境导入，初步认识

复习回顾:同学们回顾一下:

①y=ax2,y=a(x-h)2,（a≠0)的图象的开口方向、对称轴、顶点坐标，y随x的增减性分别是什么？

②如何由y=ax2(a≠0)的图象平移得到y=a(x-h)2的图象？

③猜想二次函数y=a(x-h)2+k的图象开口方向、对称轴、顶点坐标及y随x的增减性如何？

二、思考探究，获取新知

探究1  y=a(x-h)2+k的图象和性质

1.由老师提示列表，根据抛物线的轴对称性观察图象回答下列问题：

①y=-(x+1)2-1图象的开口方向、对称轴、顶点坐标及y随x的增减性如何？

②将抛物线y=-x2向左平移1个单位，再向下平移1个单位得抛物线

y=-(x+1)2-1.

2.同学们讨论回答：

①一般地，当h＞0,k＞0时，把抛物线y=ax2向右平移h个单位，再向上平移k个单位得抛物线y=a(x-h)2+k;平移的方向和距离由h,k的值来决定.

②抛物线y=a(x-h)2+k的开口方向、对称轴、顶点坐标及y随x的增减性如何？

探究2  二次函数y=a(x-h)2+k的应用

【教学说明】二次函数y=a(x-h)2+k的图象是，对称轴是，顶点坐标是，当a＞0时，开口向，当a＜0时，开口向.

答案：抛物线，直线x=h,(h,k),上，下

三、典例精析，掌握新知

例1 已知抛物线y=a(x-h)2+k,将它沿x轴向右平移3个单位后，又沿y轴向下平移2个单位，得到抛物线的解析式为y=-3(x+1)2-4,求原抛物线的解析式. 

【分析】平移前后抛物线的形状,大小不变,所以a=-3,平移时应抓住顶点的变化，根据平移规律可求出原抛物线顶点，从而得到原抛物线的解析式.

解:抛物线y=-3(x+1)2-4的顶点坐标为（-1,-4),它是由原抛物线向右平移3个单位，向下平移2个单位而得到的，所以把现在的顶点向相反方向移动就得到原抛物线顶点坐标为（-4，-2).故原抛物线的解析式为y=-3(x+4)2-2.

【教学说明】抛物线平移不改变形状及大小，所以a值不变，平移时抓住关键点：顶点的变化.

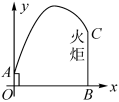例2 如图是某次运动会开幕式点燃火炬时的示意图，发射台OA的高度为2m，火炬的高度为12m,距发射台OA的水平距离为20m,在A处的发射装置向目标C发射一个火球点燃火炬，该火球运行的轨迹为抛物线形，当火球运动到距地面最大高度20m时，相应的水平距离为12m.请你判断该火球能否点燃目标C？并说明理由.

【分析】建立适当直角坐标系,构建二次函数解析式,然后分析判断.

解:该火球能点燃目标.如图,以OB所在直线为x轴，OA所在直线为y轴建立直角坐标系，则点（12，20）为抛物线顶点，设解析式为y=a(x-12)2+20,∵点（0，2）在图象上，∴144a+20=2,∴a=- ,∴y=- (x-12)2+20.当x=20时，y=-×(20-12)2+20=12,即抛物线过点（20,12),∴该火球能点燃目标.

【教学说明】二次函数y=a(x-h)2+k的应用关键是构造出二次函数模型.

四、运用新知，深化理解

1.若抛物线y=-7(x+4)2-1平移得到y=-7x2,则必须（    ）

A.先向左平移4个单位，再向下平移1个单位

B.先向右平移4个单位，再向上平移1个单位

C.先向左平移1个单位，再向下平移4个单位

D.先向右平移1个单位，再向上平移4个单位

2.抛物线y=x2-4与x轴交于B,C两点，顶点为A，则△ABC的周长为（    ）

A.4       B.4+4      C.12    D.2+4

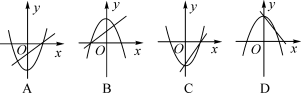
3.函数y=ax2-a与y=ax-a(a≠0)在同一坐标系中的图象可能是（    ）

4.二次函数y=-2x2+6的图象的对称轴是         ，顶点坐标是         ，当x         时，y随x的增大而增大.

5.已知函数y=ax2+c的图象与函数y=-3x2-2的图象关于x轴对称，则a=         ,c=         .

6.把抛物线y=(x-1)2沿y轴向上或向下平移，所得抛物线经过Q（3，0），求平移后抛物线的解析式.

【教学说明】学生自主完成，加深对新知的理解，教师引导解疑.

【答案】1.B  2.B  3.C  4.y轴，（0，6），＜0  5.3,2  6.y=(x-1)2-4

五、师生互动，课堂小结

1.这节课你学到了什么，还有哪些疑惑？

2.在学生回答的基础上，教师点评：①二次函数y=a(x-h)2+k的图象与性质；②如何由抛物线y=ax2平移得到抛物线y=a(x-h)2+k.

【教学说明】教师应引导学生自主小结，加深理解掌握y=ax2与y=a(x-h)2+k二者图象的位置关系.

1.教材P15第1~3题.

2.完成同步练习册中本课时的练习.

掌握函数y=ax2,y=a(x-h)2,y=a(x-h)2+k图象的变化关系，从而体会由简单到复杂的认识规律.