北师大版九年级上册1 菱形的性质与判定精品表格课后测评

这是一份北师大版九年级上册1 菱形的性质与判定精品表格课后测评，共3页。
教师 授课时间年  月  日课时1课题菱形的性质和判定课型新授教学目的1.经历探索、猜测和证明的过程，理解并掌握菱形的判定条件2.能运用菱形的判定方法解决问题重点菱形判定方法的掌握难点菱形判定方法的灵活应用和选择 教学环节说明备注            教学内容    复习回顾1. 下列图形中，即是中心对称图形又是轴对称图形的是（  B ）A．等边三角形 B．菱形C．等腰梯形D．平行四边形2. 菱形的两条对角线长分别为6cm和8cm，则菱形的边长是5cm，面积为 24cm2      3. 菱形ABCD的两条对角线AC,BD相交于O，∠ADO比∠DAO大18°，则∠BCD ＝72°，∠ABC＝ 108°  ；              课程讲授               课程讲授  问题1：回顾菱形的定义及其性质。说一说性质的逆命题他们是真命题吗？定义判定法1：有一组 邻边相等 的 平行四边形 是菱形. 符号语言：∵AB=BC，四边形ABCD是平行四边形    ∴四边形ABCD是菱形 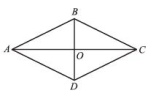问题2：用一长一短的两根木条，在它们的中点处固定一个小钉，做成一个可转动的十字，四周围上一根橡皮筋，做成一个四边形，转动木条，这个四边形什么时候变成菱形？ 已知：ABCD中，对角线AC、BD互相垂直求证：四边形ABCD是菱形分析：利用垂直平分线的性质来证明 2.菱形判定法2：对角线互相  垂直 的  平行四边形 是菱形。符号语言：∵AC⊥BD，四边形ABCD是平行四边形         ∴四边形ABCD是菱形 画一画：过一点A，作两条等长的线段AB、AD，然后分别以B、D为圆心，AB长为半径画弧，得到两弧的交点C，链接BC、CD，就得到了一个四边形，猜一猜这是什么四边形？ 3.菱形的判定方法3：四边都  相等  的 四边形 是菱形如何证明呢？请学生课下自己书写证明过程。 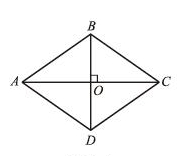 例1.如图，四边形ABCD中，AB∥CD，AC平分∠BAD，CE∥AD交AB于点E，求证四边形AECD是菱形。 （可用多种方法，比较那种简单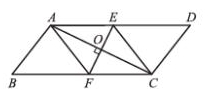）  例2. 已知:如图,在□ABCD中,对角线AC的垂直平分线分别与AD、AC、BC相较于点E、O、F.求证: 四边形AECF是菱形分析：证明△AOE≌△C0F     得到AE=CF，再通过垂直平分线的性质得出四边都相等，从而证明是菱形                                  课堂练习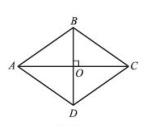1、下列命题：（1）四边都相等的四边形是菱形；（2）两组邻边分别相等的四边形是菱形；（3）对角线互相垂直的平行四边形是菱形；（4）对角线相等的四边形是菱形（5）一条对角线平分一组对角的平行四边形是菱形.其中正确的命题是 (1)(3)(5) （填写序号）2、如图，要使平行四边形ABCD成为菱形，则需要添加的条件是（ C ）A．AB=CD  B．AD=BC  C．AB=BC      D．AC=BD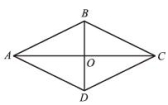3、如图，在ABCD中，对角线AC与BD相交于点O，AB＝10，OA＝8，OB＝6    求证：ABCD是菱形   小结1、菱形的判定方法有几种？分别是什么？2、菱形判定方法的选择：(1)当已知四边形是平行四边形，可以再证明一组邻边相等或对角线互相垂直(2)如果不知道是平行四边形时，可以直接证明四边相等，或者先证明它是平行四边形再进一步证明其是菱形  作业布置优化设计的相应练习，注意挑选题目 课后反思