教师			授课时间	年月日	课时	1
课题	1.3.2 正方形的判定				课型	新授
教学目的	1.理解和掌握正方形的5中判定方法，并能书写出证明推理的过程 2.正确理解正方形、菱形、矩形以及平行四边形之间的关系
重点	正方形的判定
难点	正方形的判定的灵活应用
	教学环节	说明					备注
教学内容	复习回顾	1. 正方形是菱形，是矩形（填“是”或“不是”） 2. 正方形具有而矩形不一定具有的性质是（B ） A.四个角相等 B.对角线互相垂直 C.对角互补 D.对角线相等 3．正方形具有而菱形不一定具有的性质是（ D ） A.四条边相等 B.对角线互相垂直平分 C.对角线平分一组对角 D.对角线相等					明确正方形、菱形、矩形的性质区别，有助于判定的学习
	课程讲授课程讲授	问题1：你觉得什么样的四边形是正方形？（判定一个四边形是正方形有哪些方法？）（可从平行四边形、菱形、矩形作为出发点）问题2：（小组讨论）思考并在箭头上填上相应的条件，使得平行四边形是正方形? 1．正方形判定法（定义法）：有一组邻边相等，并且有一个角是直角的平行四边形是正方形. 即可先判定一个四边形是平行四边形，若其中有一个角是直角，并且有一组邻边相等，则它是正方形。由定义法，其实可以延伸出正方形的其他的判定：正方形判定法1：有一组邻边相等的矩形是正方形；正方形判定法：对角线相等的菱形是正方形；正方形判定法3：有一个角是直角的菱形是正方形正方形判定法4：对角线互相垂直的矩形是正方形总结：既是菱形又是矩形的四边形是正方形练一练： 1.四边形ABCD中，∠A＝∠B＝∠C＝90°，如果添加一个条件，即可推出该四边形是正方形，那么这个条件可以是（） A．∠D＝90° B．AB＝CD C．AD＝BC D．BC＝CD 2.要使一个四边形是正方形，那么这个四边形的对角线（）A．垂直平分 B．垂直且相等 C．平分且相等 D．垂直、平分且相等例1．已知，如图，在矩形ABCD中，BE平分∠ABC，CE平分∠DCB，BF∥CE，CF∥BE，求证：四边形BECF是正方形。分析：此题为书本的例题，具体的解题思路可参考书本的方法。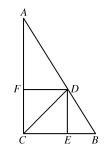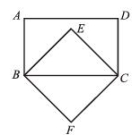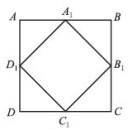跟踪练习：如图,△ABC中，∠ACB＝90°，CD平分∠ACB，DE⊥BC， DF⊥AC，垂足分别为E、F．求证：四边形CFDE是正方形．分析：先利用“三个角是直角的四边形是矩形”来说明四边形CFDE是矩形，再利用平行与平分线的关系说明，FC=FD或者CE=ED，从而说明该四边形是正方形思考：（1）依次连接四边形任意中点可以得到什么图形？（2）依次连接平行四边形或正方形或菱形或矩形又可以得到什么图形？（3）依次连接四边形各边中点所得到的新四边形的形状与哪些线段有关系？
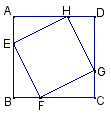
	课堂练习	1.已知□ABCD中，AB＝BC，AC＝BD，则□ABCD为，根、依据判定。 2.在正方形ABCD中，点E、F、G、H分别在各边上，且AE＝BF＝CG＝DH．四边形EFGH是正方形吗?为什么?
	小结	明确5种正方形的判定方法： ①相等邻边+直角+平行四边形=正方形（定义） ②菱形+对角线相等=正方形 ③矩形+对角线垂直=正方形 ④一个角为直角+菱形=正方形 ⑤一组邻边相等+矩形=正方形
	作业布置	优化设计的相应练习，注意挑选题目
课后反思