初中数学北师大版九年级上册5 相似三角形判定定理的证明优秀表格巩固练习
展开![]() 《相似三角形判定定理的证明》教学设计
《相似三角形判定定理的证明》教学设计
【教材】北师大九年级上第四章第五节 相似三角形判定定理的证明
【课时安排】第1课时
【教学对象】九年级学生
【教材分析】本节课的内容是“探索三角形相似的条件”之后的一个学习内容,学生已经学习了相似三角形的有关知识。本节课从证明相似三角形判定定理1、两角分别相等的两个三角形相似入手,使学生进一步通过推理证明上节课所得结论命题1的正确性,从而学会证明的方法,为后续证明判定定理2,3打下基础,感受转化的数学思想方法,感悟定理证明的完备性。
【学情分析】学生已经学习了相似三角形的有关知识,对相似三角形已经有了一定的认识,并且在前一节课的学习中,已充分经历了猜想,动手操作,得出结论的过程。本节主要进行相似三角形判定定理的证明,证明过程中需添加辅助线,对学生来说具有挑战性,需要通过已有的知识储备,相似三角形的定义以及构造三角形全等的方法完成证明过程。
【教学目标】了解相似三角形判定定理的证明过程,发展推理能力。
【教学重点】 相似三角形判定定理的证明。
【教学难点】判定定理的证明,如何添加辅助线。
【教学方法】引导探究。
【教学过程设计】
一、教学流程



![]()
![]()



![]()
![]()


![]()
![]()


![]()
![]()

![]()

![]()
![]()


二、教学过程
教学 环节 | 教 学 内 容 | 教师 活动 | 学生 活动 |
(一) 知识回顾
| 问题1:平行线分线段成比例定理及推论是什么? 问题2:相似三角形的定义是什么? 问题3:相似三角形的判定方法有哪些? 设计意图:复习平行线成比例定理以及相似三角形的定义,为后面的证明做好铺垫。 | 教师递进提问,与学生对话,为后续证明提供储备。 |
学生思考,回答问题 |
(二) 热身训练 |
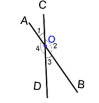
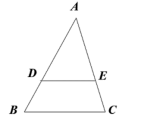
问题4:根据相似多边形的定义,△ADE与△ABC相似必须满足哪些条件? 问题5:已经具备哪些条件?为什么?还需要什么条件? 问题6:解决这个问题的关键在哪里?怎么解决? 问题7:由此你能得出什么结论?如果这条直线与三角形两边的延长线相交呢? 设计意图: 通过递进式的问题串,引发学生思考,感受波利亚解题分析法,步步推进,找到证明思路。由此预备定理得证,为后面判定定理1的证明提供方向。 |
教师引导学生分析题目,利用波利亚解题法分析问题,找到证明思路。 |
学生先自主思考后回答以上问题。 |
(三) 定理证明
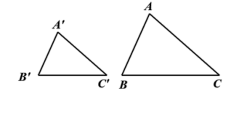
| 已知:如图,在 △ABC 和△A'B'C' 中,∠A = ∠A',∠B =∠B'.
问题8:要证明两个三角形相似,需要什么条件?已经具备什么条件?还需要哪些条件?解决这个问题的关键在哪里?怎么解决?
追问:能否把大的△ABC转化到小的△ A ' B ' C '外? 设计意图:利用波利亚解题分析法,找到相似三角形判定定理的证明方法,体会转化思想,通过构造全等三角形把两个三角形放在一起,转化为已经解决的的热身训练,使问题得解。再通过追问,引导学生学会思考问题的完整性。 |
引导学生学会分析问题,化解辅助下你构造全等三角形的难点 |
学生思考后递进回答,感悟转化的思想方法 |
(四) 典例精析
|
设计意图:利用强两个例题巩固判定定理1的应用,例3在于巩固本节课的波利亚解题分析法。 |
教师 通过例题,提升学生综合运用知识和说理分析的能力。
|
学生 通过独立完成 |
(五) 巩固训练
|
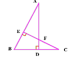
练习2.已知:如图,∠ABD=∠C,AD=2, AC=8,求AB.
求证:△ABF∽△DFE |
教师给学生足够的空间和思考时间。 |
思考回答
|
(六) 课堂小结 | 本节课你收获了什么知识点? 如何分析证明题找到思路? 在研究过程中还收获了什么数学思想方法? 设计意图:梳理知识,反思波利亚解题分析法,感悟数学转化思想方法。 |
引导归纳 | 巩固所学知识,感悟思想方法 |
初中数学北师大版九年级上册5 相似三角形判定定理的证明课后练习题: 这是一份初中数学北师大版九年级上册5 相似三角形判定定理的证明课后练习题,共7页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
初中数学北师大版九年级上册第五章 投影与视图2 视图精品表格同步训练题: 这是一份初中数学北师大版九年级上册第五章 投影与视图2 视图精品表格同步训练题,共10页。
初中数学北师大版九年级上册1 投影精品表格同步训练题: 这是一份初中数学北师大版九年级上册1 投影精品表格同步训练题,共4页。