


2022--2023学年北师大版七年级下册数学期末练习题
展开
这是一份2022--2023学年北师大版七年级下册数学期末练习题,共10页。
![]() 北师大版七年级下册数学期末练习试题考试时间:90分钟 满分:150分 第一部分 客观题(请用2B铅笔将正确答案涂在答题卡对应的位置上) 一、选择题(下列各题的备选答案中,只有一个答案是正确的,每小题3分,共24分)1.以下有四个事件:①抛一枚匀质硬币,正面朝上;②掷一枚匀质骰子,所得的点数为3;③从一副54张扑克牌中任意抽出一张恰好为红桃;④从装有1个红球,2个黄球的袋中随意摸出一个球,这两种球除颜色外其他都相同,结果恰好是红球.按概率从小到大顺序排列的结果是( ) A. ①<②<③<④ B. ②<③<④<① C. ②<①<③<④
北师大版七年级下册数学期末练习试题考试时间:90分钟 满分:150分 第一部分 客观题(请用2B铅笔将正确答案涂在答题卡对应的位置上) 一、选择题(下列各题的备选答案中,只有一个答案是正确的,每小题3分,共24分)1.以下有四个事件:①抛一枚匀质硬币,正面朝上;②掷一枚匀质骰子,所得的点数为3;③从一副54张扑克牌中任意抽出一张恰好为红桃;④从装有1个红球,2个黄球的袋中随意摸出一个球,这两种球除颜色外其他都相同,结果恰好是红球.按概率从小到大顺序排列的结果是( ) A. ①<②<③<④ B. ②<③<④<① C. ②<①<③<④ ![]() D. ③<②<①<④
D. ③<②<①<④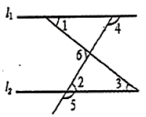 2.如图,下列条件:①∠1=∠2;②∠4=∠5;③∠2+∠5=180°;④∠1=∠3;⑤∠6+∠4=180°.其中能判断直线
2.如图,下列条件:①∠1=∠2;②∠4=∠5;③∠2+∠5=180°;④∠1=∠3;⑤∠6+∠4=180°.其中能判断直线![]() ‖
‖![]() 的有( ) A. ②③④
的有( ) A. ②③④ ![]() B. ②③⑤ C. ②④⑤ D. ②④3.下列运算正确的是( ) A. 3a+2a=5a2 B. 3a2﹣2a=a
B. ②③⑤ C. ②④⑤ D. ②④3.下列运算正确的是( ) A. 3a+2a=5a2 B. 3a2﹣2a=a
C. (﹣a)3•(﹣a2)=﹣a5 D. (2a3b2﹣4ab4)÷(﹣2ab2)=2b2﹣a2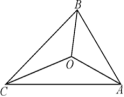 4.如图,△ABC 的三边 AB、BC、CA 长分别是 10、15、20, 其三条角平分线将△ABC 分为三个三角形,则 S△ABO:S△BCO: S△CAO 等于( ) A. 1∶1∶1 B. 1∶2∶3
4.如图,△ABC 的三边 AB、BC、CA 长分别是 10、15、20, 其三条角平分线将△ABC 分为三个三角形,则 S△ABO:S△BCO: S△CAO 等于( ) A. 1∶1∶1 B. 1∶2∶3 ![]() C. 2∶3∶4
C. 2∶3∶4 ![]() D. 3∶4∶55.已知实数a,b满足a+b=2,ab=
D. 3∶4∶55.已知实数a,b满足a+b=2,ab=![]() ,则a-b的结果是( ) A. 1
,则a-b的结果是( ) A. 1 ![]() B. -
B. - ![]()
![]() C. ±1
C. ±1 ![]() D. ±
D. ±![]() 6.有4根小木棒,长度分别为2cm、3cm、4cm、5cm,任意取3根小木棒首尾相接搭三角形,可搭出不同的三角形的个数为( )
6.有4根小木棒,长度分别为2cm、3cm、4cm、5cm,任意取3根小木棒首尾相接搭三角形,可搭出不同的三角形的个数为( ) 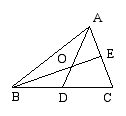 A. 1个 B. 2个 C. 3个 D. 4个7.如图,△ABC的两条中线AD、BE,交于点O,若△BOD的面积为3,则四边形DCEO的面积为A.5 B.6 C.7 D.8
A. 1个 B. 2个 C. 3个 D. 4个7.如图,△ABC的两条中线AD、BE,交于点O,若△BOD的面积为3,则四边形DCEO的面积为A.5 B.6 C.7 D.8  如图,AB∥EF , 则∠A、∠C、∠D、∠E满足的数量关系是( )A. ∠A+∠C+∠D+∠E=360° B. ∠A+∠D=∠C+∠E
如图,AB∥EF , 则∠A、∠C、∠D、∠E满足的数量关系是( )A. ∠A+∠C+∠D+∠E=360° B. ∠A+∠D=∠C+∠E
C. ∠A-∠C+∠D+∠E=180° D. ∠E-∠C+∠D-∠A=90° 第二部分 主观题(请用0.5mm黑色签字笔将答案写在答题卡对应的位置上)二、填空题(每小题3分,共24分)9.甲型H1N1流感病毒的直径约是0.00000011米,用科学记数法表示为________米. 10.如果一张长方形的纸条,如图所示折叠,那么∠α等于________. 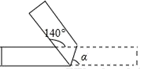 11.一个圆柱的高为8cm,则圆柱体的体积Vcm3与底面直径Rcm的关系式为________,当R为5cm时,V=________cm3 .
11.一个圆柱的高为8cm,则圆柱体的体积Vcm3与底面直径Rcm的关系式为________,当R为5cm时,V=________cm3 . 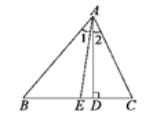 12.已知一个等腰三角形的周长是13cm,若其中一边长为3cm,则另外两边长分别是________ 13.已知
12.已知一个等腰三角形的周长是13cm,若其中一边长为3cm,则另外两边长分别是________ 13.已知![]() ,则
,则![]() =________. 14.如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠1=30°,∠2=20°,则∠B=________.
=________. 14.如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠1=30°,∠2=20°,则∠B=________. 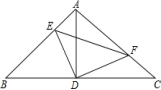 如图,Rt△ABC中,∠BAC=90°,AB=AC,点D为BC的中点,点E、F分别在边AB和边AC上,且∠EDF=90°,则下列结论一定成立的是________ ①△ADF与△BDE全等;②S四边形AEDF=
如图,Rt△ABC中,∠BAC=90°,AB=AC,点D为BC的中点,点E、F分别在边AB和边AC上,且∠EDF=90°,则下列结论一定成立的是________ ①△ADF与△BDE全等;②S四边形AEDF= ![]() S△ABC;③BE+CF=AD;④EF=AD
S△ABC;③BE+CF=AD;④EF=AD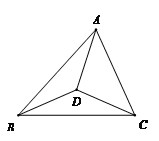 如图,在△ABC内,三边垂直平分线交点为D,若∠BAC=50°,则∠BDC的度数为 ________. 三、计算题:(第17题(1)5分,(2)、(3)6分,第18题7分,共24分) 17.要求:(1)、(2)利用乘法公式计算(1)
如图,在△ABC内,三边垂直平分线交点为D,若∠BAC=50°,则∠BDC的度数为 ________. 三、计算题:(第17题(1)5分,(2)、(3)6分,第18题7分,共24分) 17.要求:(1)、(2)利用乘法公式计算(1)![]() ; (2)20032; (3)
; (2)20032; (3)![]() . 18.先化简,再求值:
. 18.先化简,再求值: ![]() 四、作图题(第19题12分)19.如图,在正方形网格上有一个三角形 ABC(三个顶点均在格点上) (1)画出△ABC 关于直线DE对称的△A1B1C1(其中点A 与点 A1对应,点B与点B1对应,点C 与点C1对应) (2)若每个小正方形的边长都是1,计算△A1B1C1的面积.
四、作图题(第19题12分)19.如图,在正方形网格上有一个三角形 ABC(三个顶点均在格点上) (1)画出△ABC 关于直线DE对称的△A1B1C1(其中点A 与点 A1对应,点B与点B1对应,点C 与点C1对应) (2)若每个小正方形的边长都是1,计算△A1B1C1的面积. 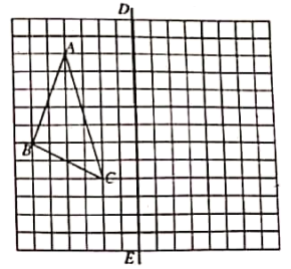 五、解答题:(第20题12分,第21题12分,共24分)20.小明所在年级有12个班,每班40名同学.学校将从该年级随机抽出一个班组建运动会入场式鲜花队,并在该班中再随机抽出1名同学当鲜花队的引导员.问: (1)小明当鲜花队的队员的概率是多少? (2)小明抽中引导员的概率是多少? (3)若小明所在班被抽中了鲜花队,那么小明抽中引导员的概率是多少? 21..小明某天上午9时骑自行车离开家,15时回家,他有意描绘了离家的距离与时间的变化情况(如图所示)
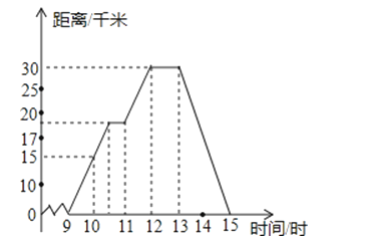
五、解答题:(第20题12分,第21题12分,共24分)20.小明所在年级有12个班,每班40名同学.学校将从该年级随机抽出一个班组建运动会入场式鲜花队,并在该班中再随机抽出1名同学当鲜花队的引导员.问: (1)小明当鲜花队的队员的概率是多少? (2)小明抽中引导员的概率是多少? (3)若小明所在班被抽中了鲜花队,那么小明抽中引导员的概率是多少? 21..小明某天上午9时骑自行车离开家,15时回家,他有意描绘了离家的距离与时间的变化情况(如图所示)
(1)图象表示了哪两个变量的关系?哪个是自变量?哪个是因变量?
(2)10时和13时,他分别离家多远?
(3)他到达离家最远的地方是什么时间?离家多远?
(4)11时到12时他行驶了多少千米?
(5)他可能在哪段时间内休息,并吃午餐?(6)他由离家最远的地方返回时的平均速度是多少?
 六、(第22题12分,第23题14分)22.完成下列证明:如图,已知
六、(第22题12分,第23题14分)22.完成下列证明:如图,已知 ![]() ,
,![]() ,∠1=∠2 .
,∠1=∠2 . 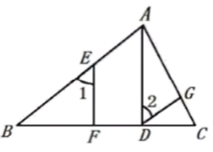 求证:∠BAC + ∠AGD=180°. 证明:∵
求证:∠BAC + ∠AGD=180°. 证明:∵ ![]() ,
,![]() (已知)∴∠EFB=90°,∠ADB=90°( ) ∴∠EFB=∠ADB(等量代换)∴EF‖AD( )∴∠1=∠BAD ( )又 ∵ ∠1=∠2 (已知)∴∠ ______ =∠ _______(等量代换)∴DG‖BA (________)∴∠BAC+ ∠AGD=180°(__________).23.如图,在 ∆ABC 和 ∆DEF 中,点 B 、 E 、 C 、 F 在同一直线上,请你从以下4个等式中选出3个作为已知条件,余下的1个作为结论,并说明结论正确的理由(写出各种可能的情况,并选择其中一种说理).
(已知)∴∠EFB=90°,∠ADB=90°( ) ∴∠EFB=∠ADB(等量代换)∴EF‖AD( )∴∠1=∠BAD ( )又 ∵ ∠1=∠2 (已知)∴∠ ______ =∠ _______(等量代换)∴DG‖BA (________)∴∠BAC+ ∠AGD=180°(__________).23.如图,在 ∆ABC 和 ∆DEF 中,点 B 、 E 、 C 、 F 在同一直线上,请你从以下4个等式中选出3个作为已知条件,余下的1个作为结论,并说明结论正确的理由(写出各种可能的情况,并选择其中一种说理). 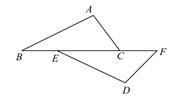 ① AB=DE; ② AC=DF; ③ ∠ABC=∠DEF; ④ BE=CF. 七、(第24题16分)24.如图,在等腰△ABC中,AB=AC=3cm , ∠B=30°,点D在BC边上由C向B匀速运动(D不与B、C重合),匀速运动速度为1cm/s , 连接AD , 作∠ADE=30°,DE交线段AC于点E .
① AB=DE; ② AC=DF; ③ ∠ABC=∠DEF; ④ BE=CF. 七、(第24题16分)24.如图,在等腰△ABC中,AB=AC=3cm , ∠B=30°,点D在BC边上由C向B匀速运动(D不与B、C重合),匀速运动速度为1cm/s , 连接AD , 作∠ADE=30°,DE交线段AC于点E . 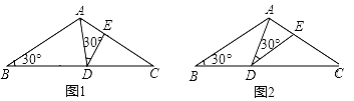 (1)在此运动过程中,∠BDA逐渐变________(填“大”或“小”);D点运动到图1位置时,∠BDA=75°,则∠BAD=________. (2)点D运动3s后到达图2位置,求CD的长 . 此时△ABD和△DCE是否全等,请说明理由; (3)在点D运动过程中,△ADE的形状也在变化,判断当△ADE是等腰三角形时,∠BDA等于多少度?(请直接写出结果) 七年级数学答案(若有其它答案,按此标准赋分)一. 选择题:1. D 2.D 3. D 4. C 5. C 6. C 7.B 8. C 二、填空题:9. 1.1×10-7 10. 70° 11. V=2πR2;50π 12. 5cm,5cm 13. 5 14. 50° 15. ①② 16. 100°
(1)在此运动过程中,∠BDA逐渐变________(填“大”或“小”);D点运动到图1位置时,∠BDA=75°,则∠BAD=________. (2)点D运动3s后到达图2位置,求CD的长 . 此时△ABD和△DCE是否全等,请说明理由; (3)在点D运动过程中,△ADE的形状也在变化,判断当△ADE是等腰三角形时,∠BDA等于多少度?(请直接写出结果) 七年级数学答案(若有其它答案,按此标准赋分)一. 选择题:1. D 2.D 3. D 4. C 5. C 6. C 7.B 8. C 二、填空题:9. 1.1×10-7 10. 70° 11. V=2πR2;50π 12. 5cm,5cm 13. 5 14. 50° 15. ①② 16. 100°
三、计算题:(第17题(1)5分,(2)、(3)6分,第18题7分,共24分) 17.(1)解:( x-y+9) (x+y-9) =x²- (y-9)² ----------------3分 =x²-y²+18y-81 -----------5分 (2)解:20032 =(2000+3)2 ----------------------------------2分=4000000+12000+9 ----------------4分 =4012009 -------------------------------6分 (3)原式= ![]() ----------3分 =37. ----------6分 18.解:原式=a2﹣2ab﹣b2﹣a2+b2---------------------2分=﹣2ab, -------------4分 当a=1,b=﹣2时, 原式=4 -----------------7分 四、作图题(第19题12分)19.【答案】 (1)解:如图△A1B1C1为所求;
----------3分 =37. ----------6分 18.解:原式=a2﹣2ab﹣b2﹣a2+b2---------------------2分=﹣2ab, -------------4分 当a=1,b=﹣2时, 原式=4 -----------------7分 四、作图题(第19题12分)19.【答案】 (1)解:如图△A1B1C1为所求; 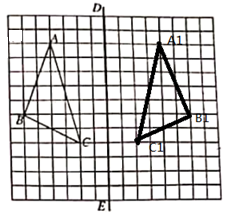 -------------------6分
-------------------6分![]() (2)解:
(2)解: ![]() 答:△A1B1C1的面积为12.-------------------------12分
答:△A1B1C1的面积为12.-------------------------12分 ![]() 五、解答题:(第20题12分,第21题12分,共24分)
五、解答题:(第20题12分,第21题12分,共24分)![]() 20【答案】 (1)小明当鲜花队的队员的概率是 -------4分
20【答案】 (1)小明当鲜花队的队员的概率是 -------4分
![]() (2)小明抽中引导员的概率是 ---------------8分
(2)小明抽中引导员的概率是 ---------------8分
(3)若小明所在班被抽中了鲜花队,那么小明抽中引导员的概率是 ----12分 解:(1)由函数图象,得图象表示了时间、距离的关系,自变量是时间,因变量是距离;
(2)由纵坐标看出10时他距家15千米,13时他距家30千米;------------2分
(3)由横坐标看出12:00时离家最远,由纵坐标看出离家30千米;------4分
(4)由纵坐标看出11时距家19千米,12时距家30千米,11时到12时他行驶了30﹣19=11(千米);---------------6分
(5)由纵坐标看出12:00﹣13:00时距离没变且时间较长,得12:00﹣13:00休息并吃午饭;-------------------8分
(6)由横坐标看出回家时用了2两小时,由纵坐标看出路程是30千米,回家的速度是30÷2=15(千米/小时).-------------------- -12分 六、(第22题12分,第23题14分)22.解: ![]() ,
, ![]() (已知),
(已知), ![]() ,
, ![]() (垂直定义),---------------2分
(垂直定义),---------------2分![]() (等量代换),
(等量代换),![]() (同位角相等,两直线平行),------------------4分
(同位角相等,两直线平行),------------------4分![]() (两直线平行,同位角相等),--------------------6分又
(两直线平行,同位角相等),--------------------6分又 ![]() (已知),----------------8分
(已知),----------------8分![]() (等量代换),
(等量代换),![]() (内错角相等,两直线平行),-----------------10分
(内错角相等,两直线平行),-----------------10分![]() (两直线平行,同旁内角互补).-------------------12分 23. 解:已知条件是①,②,④.结论是③. -----------------2分 说理过程:因为
(两直线平行,同旁内角互补).-------------------12分 23. 解:已知条件是①,②,④.结论是③. -----------------2分 说理过程:因为 ![]() (已知),所以
(已知),所以 ![]() (等式性质).即
(等式性质).即 ![]() .------------------6分在
.------------------6分在 ![]() 和
和 ![]() 中,
中,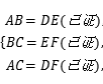 所以
所以 ![]() -----------------------12分所以
-----------------------12分所以 ![]() .-----------------------------14分 七、(第24题16分)24.(1)大;75° ---------------- 6分
.-----------------------------14分 七、(第24题16分)24.(1)大;75° ---------------- 6分
(2)解:点D运动3s后到达图2位置,CD=3cm,此时△ABD≌△DCE, 理由如下:∵AB=AC,∠B=30°,∴∠C=30°,![]() ∵CD=CA=3cm,∴∠CAD=∠CDA= ×(180°-30°)=75°,∴∠ADB=105°,∠EDC=75°-30°=45°,∴∠DEC=180°-45°-30°=105°,∴∠ADB=∠DEC,在△ABD和△DCE中,
∵CD=CA=3cm,∴∠CAD=∠CDA= ×(180°-30°)=75°,∴∠ADB=105°,∠EDC=75°-30°=45°,∴∠DEC=180°-45°-30°=105°,∴∠ADB=∠DEC,在△ABD和△DCE中,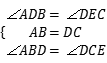 ,∴△ABD≌△DCE(ASA)--------11分
,∴△ABD≌△DCE(ASA)--------11分
(3)60°或105°. ----------16分
相关试卷
这是一份2022--2023学年北师大版七年级下册数学期末练习综合试题,共10页。试卷主要包含了选择题,填空题,计算题,作图题,解答题等内容,欢迎下载使用。
这是一份2022--2023学年北师大版七年级下册数学期末练习题,共8页。试卷主要包含了选择题,填空题,计算题,作图题,解答题等内容,欢迎下载使用。
这是一份2022--2023学年北师大版七年级下册数学期末练习综合试题,共11页。试卷主要包含了选择题,填空题,计算题,作图题,解答题等内容,欢迎下载使用。










