2021届河北省张家口市邢台市衡水市高三上学期摸底联考（新高考）数学试题（解析版）

这是一份2021届河北省张家口市邢台市衡水市高三上学期摸底联考（新高考）数学试题（解析版），共21页。
2021届河北省张家口市邢台市衡水市高三上学期摸底联考（新高考）数学试题


一、单选题
1．已知集合，，则（ ）．
A． B． C． D．
【答案】D
【解析】化简集合，利用交集的定义计算即可．
【详解】
∵，∴．
故选：D
【点睛】
本题考查集合的交并补运算，考查函数的定义域，属于基础题．
2．命题“，”的否定是（ ）．
A．， B．，
C．， D．
【答案】A
【解析】根据全称量词命题的否定为存在量词命题即可得解；
【详解】
解：命题“，”为全称量词命题，其否定为存在量词命题，所以命题的否定为：，．
故选：A．
【点睛】
本题考查全称命题的否定，属于基础题.
3．已知复数，则的共轭复数在复平面内对应的点位于（ ）．
A．第一象限 B．第二象限 C．第三象限 D．第四象限
【答案】D
【解析】化简复数，进而得出的共轭复数，可得在复平面内对应的点．
【详解】
∵，∴，它在复平面内对应的点位于第四象限．
故选：D．
【点睛】
本题考查复数的几何意义，考查共轭复数的定义，考查复数的运算，属于基础题．
4．设，，，则（ ）．
A． B． C． D．
【答案】B
【解析】先与0比较，c小于0，再a和b与1比较，即可判断大小.
【详解】

，，
，
∴．
故选：B．
【点睛】
本题考查比较大小、指数函数单调性、对数函数单调性，考查基本分析判断能力，属基础题.
5．已知向量，满足，且，则与的夹角的余弦值为（ ）．
A． B． C． D．
【答案】B
【解析】将两边平方可得，再利用向量数量积即可求解.
【详解】
∵，
∴，
∴，且，
设向量与的夹角为，
则．
故选：B．
【点睛】
本题考查了向量的数量积求向量的夹角，考查了基本知识的掌握情况以及基本运算求解能力，属于基础题.
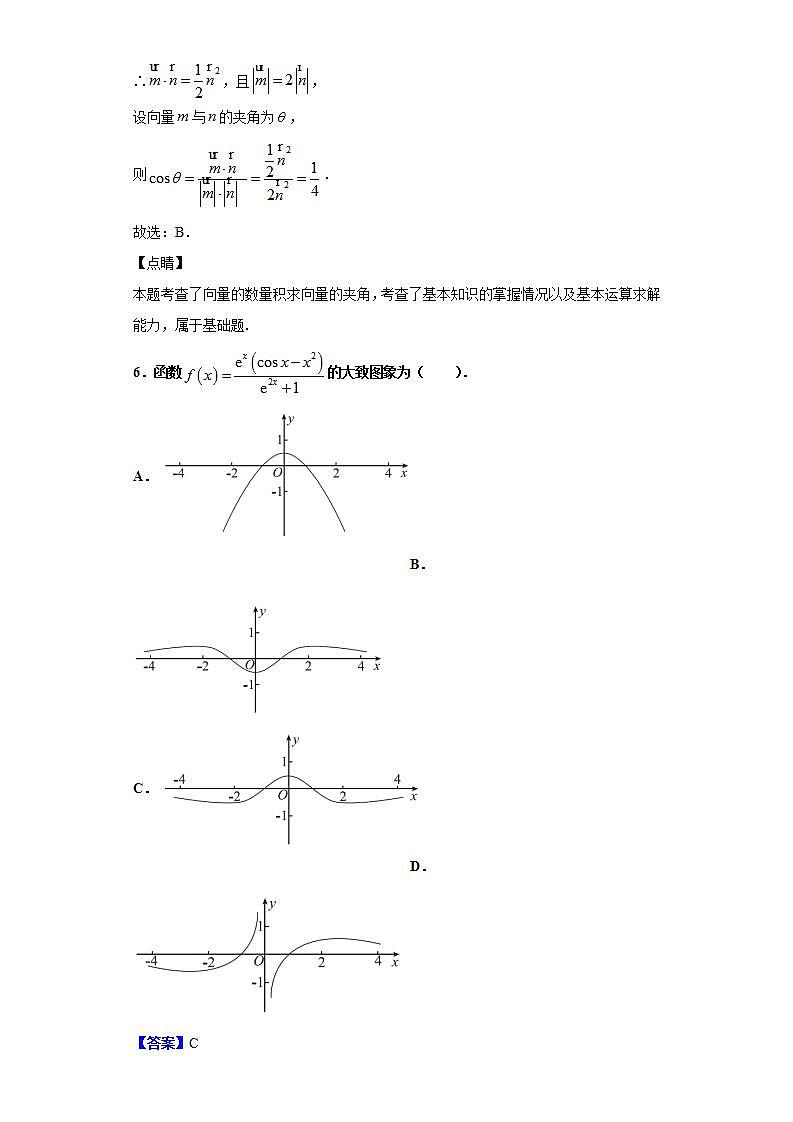
6．函数的大致图象为（ ）．
A． B．
C． D．
【答案】C
【解析】根据解析式，分析函数的定义域、奇偶性、特殊点、单调性等，利用排除法即可求出答案．
【详解】
解：∵，且定义域为，
∴为偶函数，排除D；
∵，∴排除B；
∵，而，
∴，排除A；
故选：C．
【点睛】
本题主要考查函数图象的识别问题，考查数形结合思想，属于中档题．
7．我国古代著作《庄子·天下篇》引用过一句话：“一尺之棰，日取其半，万世不竭．”其含义是：一尺长的木棍，每天截去它的一半，永远也截不完．在这个问题中，记第天后剩余木棍的长度为，数列的前项和为，则使得不等式成立的正整数的最小值为（ ）．
A．9 B．10 C．11 D．12
【答案】C
【解析】记第天后剩余木棍的长度为，则是首项为，公比为的等比数列，利用等比数列的求和公式计算，解不等式可得整数的最小值．
【详解】
记第天后剩余木棍的长度为，则是首项为，公比为的等比数列，
所以，，是关于的增函数，
而，，
所以使得不等式成立的正整数的最小值为11．
故选：C．
【点睛】
本题考查等比数列求和公式的应用，考查数列的单调性，属于基础题．
8．已知斜率存在的直线交椭圆：于，两点，点是弦的中点，点，且，，则直线的斜率为（ ）．
A． B． C． D．
【答案】D
【解析】设，，，代入椭圆的方程两式相减，整理得，再由，得到，进而根据，求得，过点作轴于点，求得，即可求得.
【详解】
设，，，直线的斜率为，不妨令，
则两式相减，得，
所以，所以，即．
由，即,可得，
又由，所以，解得，
过点作轴于点，则，
所以，即，
根据椭圆的对称性，可得直线的斜率为．
故选：D．
【点睛】
本题主要考查了椭圆的标准方程及其几何性质，以及直线的倾斜角和斜率公式的应用，着重考查了推理与运算能力，属于中档试题.

二、多选题
9．已知双曲线：（）的一条渐近线方程为，则下列说法正确的是（ ）．
A．的焦点在轴上 B．
C．的实轴长为6 D．的离心率为
【答案】AD
【解析】根据双曲线的定义及性质即可验证各选项．
【详解】
解：由，可知双曲线的焦点一定在轴上，故A正确；
根据题意得，所以，故B错误；
双曲线的实轴长为，故C错误；
双曲线的离心率，故D正确．
故选：AD．
【点睛】
本题主要考查双曲线的几何性质，属于基础题．
10．2020年初以来，技术在我国已经进入高速发展的阶段，手机的销量也逐渐上升，某手机商城统计了近5个月来手机的实际销量，如下表所示：
月份
2020年2月
2020年3月
2020年4月
2020年5月
2020年6月
月份编号
1
2
3
4
5
销量部
37
104

196
216
若与线性相关，且求得线性回归方程为，则下列说法正确的是（ ）
A．
B．与正相关
C．与的相关系数为负数
D．8月份该手机商城的手机销量约为36.5万部
【答案】AB
【解析】计算出销量的平均数，利用总销量可得值；由回归方程中的的系数为正可知，与正相关；将代入，可得8月份该手机商城的手机销量．
【详解】
由表中数据，计算得，所以，
于是得，解得，故A正确；
由回归方程中的的系数为正可知，与正相关，且其相关系数，故B正确，C错误；
8月份时，，（万部），故D错误．
故选：AB．
【点睛】
本题考查两个变量的线性相关关系，考查了线性回归方程的应用，考查学生逻辑推理能力，属于中档题．
11．已知，，且，则（ ）
A． B．
C． D．
【答案】ACD
【解析】结合不等式的基本性质，根据基本不等式逐一验证各选项即可得出结论．
【详解】
解：∵，
∴，∴，故A正确；
，∴，故B错误；
，故C正确；
，故D正确．
故选：ACD．
【点睛】
本题主要考查基本不等式的应用，考查计算能力，属于中档题．
12．已知函数与（）的图象关于轴对称，则下列结论正确的是（ ）．
A．
B．直线是的图象的一条对称轴
C．在上单调递减
D．的图象可看作是的图象向左平移个单位长度而得到的
【答案】ABC
【解析】首先求出，然后逐一判断即可.
【详解】
由题得，，
∴，故A正确；
∵，
∴直线是函数的图象的一条对称轴，故B正确；
由（），得（），
当时，，故在上单调递减，故C正确；
，
而，
故函数的图象可看作是函数的图象向右平移个单位长度而得到的，故D错误．
故选：ABC
【点睛】
本题考查的是三角函数的图象和性质，考查了学生对基础知识的掌握情况，属于中档题.


三、填空题
13．若曲线在点处的切线的斜率为1，则______．
【答案】
【解析】求得函数的导数，得到，根据题意得出，即可求解.
【详解】
由题意，函数，可得，则，
因为曲线在点处的切线的斜率为，
所以，解得．
故答案为：.
【点睛】
本题主要考查了利用导数的几何意义求参数问题，其中解答中熟记导数的几何意义，列出方程是解答的关键，着重考查运算与求解能力.
14．2020年是我国脱贫攻坚决战决胜之年，某县农业局为支持该县的扶贫工作，决定派出8名农技人员（5男3女），并分成两组，分配到2个贫困村进行扶贫工作，若每组至少3人，且每组都有男农技人员，则不同的分配方案共有______种（用数字填写答案）．
【答案】180
【解析】分为两类：第一类是一组3人，另一组5人，第二类是两组均为4人，然后根据人数分组，再进行排列即可.
【详解】
分配的方案有两类，
第一类：一组3人，另一组5人，有种；
第二类：两组均为4人，有种，
所以共有种不同的分配方案．
故填：180
【点睛】
本题考查了分类计数原理和分步计数原理以及排列组合数的计算，属于中档题目，解题中需要注意分组的条件要充分考虑到，防止重复和遗漏.
15．已知球是三棱锥的外接球，，，则当点到平面的距离取最大值时，球的表面积为______．
【答案】
【解析】当点到平面的距离最大时，平面,转化为三棱柱的外接球求解即可.
【详解】
当点到平面的距离最大时，平面．如图，
以为底面，为侧棱补成一个直三棱柱，则球是该三棱柱的外接球，
球心到底面的距离．
由正弦定理得的外接圆半径，
所以球的半径为，
所以球的表面积为．
故答案为：.

【点睛】
本题主要考查点面距离、多面体的外接球以及正弦定理的应用，属于综合题.

四、双空题
16．已知，则______，______．
【答案】3;
【解析】根据两角差的正切公式可求得第一空，再根据二倍角公式弦化切可求得第二空．
【详解】
解：∵，
∴，解得，
∴，
故答案为：3；．
【点睛】
本题主要考查两角差的正切公式，考查同角三角函数的基本关系，考查齐次式的求值，属于基础题．

五、解答题
17．在①；②；③（），这三个条件中，任选一个补充在下面问题中的横线处，并加以解答．
已知的内角，，的对边分别为，，，若，的面积为4，______，求及．
注：如果选择多个条件分别解答，按第一个解答计分．
【答案】．.
【解析】选①，用正弦定理化角为边，再用两角和公式求出，再由面积公式求出，，再由余弦定理可求出
选②，用正弦定理化角为边，再用两角和公式的求出，，再由面积公式求出，，再由余弦定理可求出
选③，利用倍角公式，两角和公式以及面积公式和余弦定理即可求解
【详解】
解：若选①：由正弦定理及，
得，
又，所以，所以，即，所以．
因为，所以，
由余弦定理得，
即．
若选②：由正弦定理得及，
得，即，
又，所以，所以，结合及，
可解得，．
因为，所以，
由余弦定理得，
即．
若选③：由，得，
又，所以，所以，
所以，
所以．
因为，所以，
由余弦定理得，
即．
【点睛】
本题考查正弦定理，余弦定理，两角和公式以及面积公式的使用，属于基础题
18．记为等差数列的前项和，，．
（1）求数列的通项公式及；
（2）记数列的前项和为，若，求的值．
【答案】（1）；；（2）．
【解析】（1）设等差数列的公差为，根据等差数列的通项公式和前项和公式即可求出答案；
（2）由（1）可得，再用裂项相消法可求得，再解方程即可求出答案．
【详解】
解：（1）设等差数列的公差为，
∵，，
∴， 解得，
∴，
∴；
（2）由（1）可得，
∴，
令，得，即，
∴．
【点睛】
本题主要考查等差数列的通项公式和前项和公式的应用，考查裂项相消法求和，属于基础题．
19．如图，在多面体中，四边形为直角梯形，，，四边形为正方形，平面平面．，为线段的中点．

（1）求证：平面；
（2）求平面与平面所成的锐二面角的余弦值．
【答案】（1）证明见解析；（2）.
【解析】（1）证明平面内的两条相交直线，即可得答案；
（2）由（1）知平面，所以，，又，可得，，两两垂直．分别以，，为轴，轴，轴的正方向建立空间直角坐标系（如图）．求出平面的法向量，再代入向量的夹角公式，即可得答案；
【详解】
解：（1）因为为正方形，所以．又因为平面平面，
且平面平面，所以平面．所以．
因为，线段的中点，所以．
又，所以平面．
（2）由（1）知平面，所以，，又，
所以，，两两垂直．分别以，，为轴，轴，轴的正方向建立空间直角坐标系（如图）．

设，则，，，，，
所以，，，设平面的一个法向量为，
则 即令，则，，则．
由（1）知，为平面的一个法向量．
设平面与平面所成的锐二面角为，
则．
所以平面与平面所成的锐二面角的余弦值为．
【点睛】
本题考查线面垂直判定定理、线面角的向量求法，考查转化与化归思想，考查空间想象能力、运算求解能力，求解时注意寻找三条两两互相垂直的直线，再建系.
20．在平面直角坐标系中，已知，，动点满足．
（1）求动点的轨迹的方程；
（2）过点作直线交于，两点，若的面积是的面积的2倍，求．
【答案】（1）；（2）.
【解析】（1）设，求得的坐标，结合，化简、整理，即可求得抛物线的方程；
（2）设，不妨设，由，求得，设直线的方程为，联立方程组，结合根与系数的关系，求得，，进而求得，利用弦长公式，即可求解.
【详解】
（1）设，因为，，
则，，．
由，可得，化简得，
即动点的轨迹的方程为．
（2）设，，
由题意知，，
易知，不妨设，
因为，所以，所以． ①
设直线的方程为，
联立消去，得，则，
可得， ②
由①②联立，解得，
所以．
【点睛】
本题主要考查了向量的坐标运算，抛物线的标准方程的求解，以及直线与抛物线的位置关系的综合应用,解答此类题目，通常联立直线方程与抛物线方程，应用一元二次方程根与系数的关系进行求解，此类问题易错点是复杂式子的变形能力不足，导致错解，能较好的考查考生的逻辑思维能力、运算求解能力、分析问题解决问题的能力等．

质量指标值





频数
20
10
30
15
25
（1）规定：消毒液的质量指标值越高，消毒液的质量越好．已求得甲厂所生产的消毒液的质量指标值的中位数为，乙厂所生产的消毒液的质量指标值的平均数为26.5，分别求甲厂所生产的消毒液的质量指标值的平均数以及乙厂所生产的消毒液的质量指标值的中位数，并针对这两家工厂所生产的消毒液的质量情况写出两条统计结论；
（2）甲厂生产的消毒液的质量指标值近似地服从正态分布，其中近似为样本平均数，并已求得．该厂决定将消毒液分为，，级三个等级，其中质量指标值不高于2.6的为级，高于38.45的为级，其余为级，请利用该正态分布模型解决下列问题：
（ⅰ）甲厂近期生产了10万瓶消毒液，试估计其中级消毒液的总瓶数；
（ⅱ）已知每瓶消毒液的等级与出厂价（单位：元/瓶）的关系如下表所示：
等级



出厂价
30
25
16
假定甲厂半年消毒液的生产量为1000万瓶，且消毒液全都能销售出去．若每瓶消毒液的成本为20元，工厂的总投资为4千万元（含引进生产线、兴建厂房等一切费用在内），问：甲厂能否在半年之内收回投资？试说明理由．
附：若，则，，．
【答案】（1）26.5；；答案见解析；（2）（ⅰ）级消毒液有81860瓶；（ⅱ）甲厂能在半年之内收回投资．理由见解析.
【解析】（1）根据频率分布直方图和频率分布表求出平均数、众数，然后对两家工厂生产的消毒液质量指标值作比较得出方案；
（2）根据模型可求出；
（3）列出的分布列，可求出期望，然后再作比较可得答案.
【详解】
（1）甲厂所生产的消毒液的质量指标值的平均数为
．
设乙厂生产的消毒液的质量指标值的中位数为，
则，解得．
统计结论：（答案不唯一，任意两个即可，其他答案如果叙述正确也给分）
①两家工厂生产的消毒液质量指标值的平均数相等，从这个角度看这两家工厂生产的消毒液质量基本相当；
②由数据波动的情况可知，乙厂生产的消毒液质量的方差大于甲厂生产的消毒液质量的方差，说明甲厂生产的消毒液比乙厂生产的消毒液的质量更稳定．
③两家工厂生产的消毒液质量指标值的平均数相同，但乙厂生产的消毒液质量的方差大于甲厂生产的消毒液质量的方差，所以甲厂生产的消毒液更好．
④两家工厂所生产的消毒液的质量指标值的众数均等于25．
⑤两家工厂所生产的消毒液的质量指标值的中位数均为．
⑥甲厂生产的消毒液质量集中在平均数附近，乙厂生产的消毒液中质量指标值特别小和质量指标值特别大的较多．
（2）（ⅰ）
，
因为，所以可估计甲厂所生产的这10万瓶消毒液中，级消毒液有81860瓶．
（ⅱ）设每瓶消毒液的利润为元，则的可能取值为10，5，，

，
由（ⅰ）知，
所以，故的分布列为

10
5


0.15865
0.8186
002275
所以每瓶消毒液的平均利润为（元），
故生产半年消毒液所获利润为（千万元），
而5．5885（千万元）4（千万元），所以甲厂能在半年之内收回投资．
【点睛】
本题考查了根据频率分布直方图、频率分布表求平均数、中位数，正态分布的性质及随机变量的分布列.
22．已知函数，．
（1）求在区间上的极值点；
（2）证明：恰有3个零点．
【答案】（1）极大值点，极小值点；（2）证明见解析.
【解析】（1）求出，利用导数求出函数的单调区间，进而求出极值点.
（2）求出是的一个零点，再判断函数为偶函数，只需确定时，的零点个数，利用导数判断函数的单调性，结合函数的符号即可求解．
【详解】
解：（1）（），
令，得，或．
当时，，单调递增；
当时，，单调递减；
当时，，单调递增．
故是的极大值点，是的极小值点．
综上所述，在区间上的极大值点为，极小值点为．
（2）（），
因为，所以是的一个零点．
，
所以为偶函数．
即要确定在上的零点个数，只需确定时，的零点个数即可．
当时，．
令，即，或（）．
时，，单调递减，又，所以；
时，，单调递增，且，
所以在区间内有唯一零点．当时，由于，．
．
而在区间内单调递增，，
所以恒成立，故在区间内无零点，
所以在区间内有一个零点，由于是偶函数，
所以在区间内有一个零点，而，
综上，有且仅有三个零点．
【点睛】
本题考查了利用导数求函数的极值点、利用导数研究函数的零点个数，考查了分析能力、数学运算，属于难题.