高考数学一轮复习作业本1.6 幂函数与二次函数（含答案）

这是一份高考数学一轮复习作业本1.6 幂函数与二次函数（含答案），共6页。
2020高考数学(理数)复习作业本1.6 幂函数与二次函数 一         、选择题1.若函数f(x)=x2＋ax＋b在区间[0，1]上的最大值是M，最小值是m，则M－m(　　)A．与a有关，且与b有关        B．与a有关，但与b无关C．与a无关，且与b无关        D．与a无关，但与b有关 2.设b＞0，二次函数y=ax2+bx+a2-1的图象是下列图象之一，则a的值为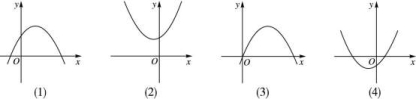（    ）A.1              B.-1            C.-1-52            D.-1+52 3.设abc＞0，二次函数f(x)=ax2＋bx＋c的图象可能是(　　) 4.已知二次函数f(x)满足f(2+x)=f(2-x),且f(x)在[0,2]上是增函数,若f(a)≥f(0),则实数a的取值范围是(　　)A.[0,+∞)                                B.(-∞,0]        C.[0,4]                                                     D.(-∞,0]∪[4,+∞)5. (2016湖南邵阳石齐中学月考)若函数f(x)=ax2+b|x|+c(a≠0)有四个单调区间,则实数a,b,c满足(　　)A.b2-4ac>0,a>0         B.b2-4ac>0       C.->0,c∈R                                   D.-<0,c∈R6.已知函数f(x)=ax2＋bx＋c，且a＞b＞c，a＋b＋c=0，集合A={m|f(m)＜0}，则(　　)A．∀m∈A，都有f(m＋3)＞0        B．∀m∈A，都有f(m＋3)＜0C．∃m0∈A，使得f(m0＋3)=0        D．∃m0∈A，使得f(m0＋3)＜0 7.已知函数f(x)=x2+2|x|,若f(-a)+f(a)≤2f(2),则实数a的取值范围是(　　)A.[-2,2]                                    B.(-2,2]                                        C.[-4,2]                                         D.[-4,4]8.已知当时，函数的图像与的图像有且只有一个交点，则正实数的取值范围是（      ）.A.                      B.C.                    D. 二         、填空题9.已知点P1(x1,2 015)和P2(x2,2 015)在二次函数f(x)=ax2+bx+9(a≠0)的图象上,则f(x1+x2)的值为　　　　.  10.当0<x<1时，幂函数y=xp的图象在直线y=x的上方，则p的取值范围是________。 11.已知函数f(x)=x2－2tx＋1，在区间[2，5]上单调且有最大值为8，则实数t的值为______． 12.已知函数f(x)=x2－2x，g(x)=ax＋2(a＞0)，对任意的x1∈[－1，2]都存在x0∈[－1，2]，使得g(x1)=f(x0)，则实数a的取值范围是________． 三         、解答题13.已知函数f(x)是定义在R上的偶函数,且当x≤0时, f(x)=x2+2x.现已画出函数f(x)在y轴左侧的图象,如图所示.(1)写出函数f(x)(x∈R)的增区间;(2)写出函数f(x)(x∈R)的解析式;(3)若函数g(x)=f(x)-2ax+2(x∈[1,2]),求函数g(x)的最小值.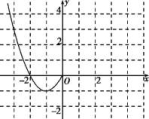   14.已知f（x）=ax2+bx+c，若f（0）=0，且f（x+1）=f（x）+x+1，求f（x）的表达式.            15.如下图所示，图1是定义在R上的二次函数f(x)的部分图象，图2是函数g(x)=loga(x＋b)的部分图象．(1)分别求出函数f(x)和g(x)的解析式；(2)如果函数y=g(f(x))在区间[1，m)上单调递减，求m的取值范围 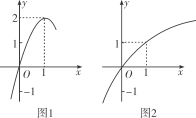         16.已知函数f(x)=ax2＋bx＋c(a>0，b∈R，c∈R)．(1)若函数f(x)的最小值是f(－1)=0，且c=1，F(x)=求F(2)＋F(－2)的值；(2)若a=1，c=0，且|f(x)|≤1在区间(0，1]上恒成立，试求b的取值范围．          
答案解析1.答案为：B.解析：设x1，x2分别是函数f(x)在[0，1]上的最小值点与最大值点，则m=x＋ax1＋b，M=x＋ax2＋b.∴M－m=x－x＋a(x2－x1)，显然此值与a有关，与b无关．故选B.2.答案：B3.答案为：D.4.C　由f(2+x)=f(2-x)可知,函数f(x)图象的对称轴为直线x==2,又因为f(x)在[0,2]上单调递增,所以由f(a)≥f(0)可得0≤a≤4.5.C　当x>0时, f(x)=ax2+bx+c,由题意知,此时, f(x)应有两个单调区间,∴->0.当x<0时, f(x)=ax2-bx+c,由<0,知x<0时f(x)有两个单调区间.∴a,b满足->0,故选C.6.答案为：A.解析：由a＞b＞c，a＋b＋c=0可知a＞0，c＜0，且f(1)=0，f(0)=c＜0，即1是方程ax2＋bx＋c=0的一个根，当x＞1时，f(x)＞0.由a＞b，得1＞，设方程ax2＋bx＋c=0的另一个根为x1，则x1＋1=－＞－1，即x1＞－2，由f(m)＜0可得－2＜m＜1，所以1＜m＋3＜4，由抛物线图象可知，f(m＋3)＞0，选A.7.A　由f(x)=x2+2|x|,知f(2)=8,则f(-a)+f(a)=2a2+4|a|≤16,解得a∈[-2,2].8.答案为:B;9.答案9解析　依题意得x1+x2=-,则f(x1+x2)=f=a+b+9=9.10.答案为：p<1.11.答案为：1.8；解析：函数f(x)=x2－2tx＋1图象的对称轴是x=t，函数在区间[2，5]上单调，故t≤2或t≥5.若t≤2，则函数f(x)在区间[2，5]上是增函数，故f(x)max=f(5)=25－10t＋1=8，解得t=1.8；若t≥5，函数f(x)在区间[2，5]上是减函数，此时f(x)max=f(2)=4－4t＋1=8，解得t=－0.75，与t≥5矛盾．综上所述，t=1.8. 12.答案为：(0,0.5]；解析：当x0∈[－1，2]时，由f(x)=x2－2x得f(x0)∈[－1，3]，又对任意的x1∈[－1，2]都存在x0∈[－1，2]，使得g(x1)=f(x0)，所以当x1∈[－1，2]时，g(x1)∈[－1，3]．当a＞0时，解得a≤.综上所述，实数a的取值范围是. 13.解析　(1)f(x)的增区间为(-1,0),(1,+∞).(2)若x>0,则-x<0,又函数f(x)是定义在R上的偶函数,且当x≤0时, f(x)=x2+2x,∴f(x)=f(-x)=(-x)2+2×(-x)=x2-2x(x>0),∴f(x)=(3)g(x)=x2-2x-2ax+2,其图象的对称轴方程为x=a+1,当a+1≤1,即a≤0时,g(1)=1-2a为g(x)在[1,2]上的最小值;当1<a+1≤2,即0<a≤1时,g(a+1)=-a2-2a+1为g(x)在[1,2]上的最小值;当a+1>2,即a>1时,g(2)=2-4a为g(x)在[1,2]上的最小值.综上,在x∈[1,2]上,g(x)min=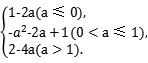14.解：∵f（0）=0，∴c=0.又∵f（x+1）=a（x+1）2+b（x+1）=ax2+2ax+a+bx+b，f（x）+x+1=ax2+bx+x+1，∴ax2+2ax+a+bx+b=ax2+bx+x+1.解得2ax+a+b=x+1.∴2a=1,a+b=1.得a=0.5,b=0.5.∴f（x）的解析式为f（x）=0.5x2+0.5x. 15.解：(1)由题图1得，二次函数f(x)的顶点坐标为(1,2)，故设函数f(x)=a(x-1)2＋2，又函数f(x)的图象过点(0,0)，故a=-2，整理得f(x)=-2x2＋4x.由题图2得，函数g(x)=loga(x＋b)的图象过点(0,0)和(1,1)，故有，所以，所以g(x)＝log2(x＋1)(x>－1)．(2)得(1)y=g(f(x))=log2(-2x2＋4x＋1)是由y=log2t和t=-2x2＋4x＋1复合而成的函数，而y=log2t在定义域上单调递增，要使函数y=g(f(x))在区间[1，m)上单调递减，必须t=-2x2＋4x＋1在区间[1，m)上单调递减，且有t>0恒成立．由t=0得x=，又t=－2x2＋4x＋1的图象的对称轴为x=1，所以满足条件的m的取值范围为1<m<. 16.解：(1)由已知c=1，a－b＋c=0，且－=－1，解得a=1，b=2，∴f(x)=(x＋1)2.∴F(x)=∴F(2)＋F(－2)=(2＋1)2＋[－(－2＋1)2]=8.(2)f(x)=x2＋bx，原命题等价于－1≤x2＋bx≤1在(0，1]上恒成立，即b≤－x且b≥－－x在(0，1]上恒成立．又－x的最小值为0，－－x的最大值为－2.∴－2≤b≤0.故b的取值范围是[－2，0]．