所属成套资源：高考数学一轮复习作业本 （含答案）
高考数学一轮复习作业本1.8 对数与对数函数（含答案）
展开
这是一份高考数学一轮复习作业本1.8 对数与对数函数（含答案），共6页。
2020高考数学(理数)复习作业本1.8 对数与对数函数一 、选择题1.
（ ）A.
B.
C.
D.
2.若当
时,函数
始终满足
,则函数
的图象大致为( )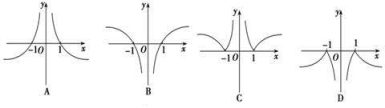
3.对数式
中，实数a的取值范围是 （ ）A．
B．(2,5) C．
D． 
4.函数f(x)=ln(x2＋1)的图象大致是( )
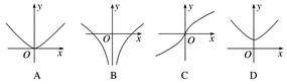A.选项A B.选项B C.选项C D.选项D5.已知函数
，若实数x0是方程f(x0)=0解，且0＜x1＜x0，则f(x1)值( )A.等于0 B.恒为负值 C.恒为正值 D.不能确定6.已知a=log29－log2，b=1＋log2，c=＋log2，则a，b，c的大小关系为( )A．a＞b＞c B．b＞a＞c C．c＞a＞b D．c＞b＞a 7.函数f(x)=-e-ln∣x∣+x的大致图象为( )
8.若函数f(x)=logm(m-x)在区间[4,5]上的最大值比最小值大1，则实数m=（ ）.A.
B.或
C.
或
D. 二 、填空题9.比较下列各组数中两个值的大小：（1）
；（2）
；（3）
；（4）
；（5）
；（6）
10.集合
和
，且A=B，则x=________，y=________ 11.已知函数
在
上的最大值比最小值多1，求实数a的值 。 12.已知函数y=lo
(x2-ax+a)在区间(-∞,
]上是增函数,则实数a的取值范围是 . 三 、解答题13.设函数
.(1)确定函数f (x)的定义域；(2)判断函数f (x)的奇偶性；(3)证明函数f (x)在其定义域上是单调增函数；(4)求函数f(x)的反函数. 14.已知y=f(x)是定义在R上的偶函数，当x
0时，f(x)=log2(x+1).(1)求当x<0时，f(x)的解析式；(2)作出函数f(x)的图象，并指出其单调区间.
15.已知函数
.(1)求函数f (x)的定义域；(2)求函数f (x)的值域. 16.已知函数f(x)=3－2log2x，g(x)=log2x.(1)当x∈[1，4]时，求函数h(x)=[f(x)＋1]·g(x)的值域；(2)如果对任意的x∈[1，4]，不等式f(x2)·f()＞k·g(x)恒成立，求实数k的取值范围．
答案解析1.答案为：C.2.答案为：B.3.D4.答案为：A.5.C. 6.答案为：B；解析：选B.a=log29－log2=log2(3)，b=1＋log2=log2(2)，c=＋log2=log2，因为函数y=log2x在(0，＋∞)上是增函数，且2＞3＞，所以b＞a＞c.7.B 8.答案为：D 9.答案为：（1）<（2）<（3）<（4）<（5）<（6）< 10.x=y=-111.答案为：0.5或2.12.答案 [2,2+2)解析 设g(x)=x2-ax+a,由于y=lo
g(x)在区间(-∞,]上是增函数,故在区间(-∞,]上,g(x)应是减函数,且g(x)>0.故有
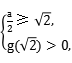即
解得
∴2≤a<2+2.故实数a的取值范围是[2,2+2).13.解： (1)由
得x∈R，定义域为R. (2)是奇函数. (3)设x1，x2∈R，且x1＜x2，则
. 令
，则
.=
=
=
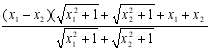∵x1－x2＜0，
，
，
，∴t1－t2＜0，∴0＜t1＜t2，∴
，∴f (x1)－f (x2)＜lg1=0，即f (x1)＜f (x2)，∴ 函数f(x)在R上是单调增函数.(4)反函数为
(x
R).14.解：
15.解：(1)函数的定义域为(1，p).(2)当p＞3时，f (x)的值域为(－∞，2log2(p+1)－2)；当1＜p
3时，f (x)的值域为(－
，1+log2(p+1)).16.解：(1)h(x)=(4－2log2x)·log2x=－2(log2x－1)2＋2，因为x∈[1，4]，所以log2x∈[0，2]，故函数h(x)的值域为[0，2]．(2)由f(x2)·f()＞k·g(x)，得(3－4log2x)(3－log2x)＞k·log2x， 令t=log2x，因为x∈[1，4]，所以t=log2x∈[0，2]，所以(3－4t)(3－t)＞k·t对一切t∈[0，2]恒成立，①当t=0时，k∈R；②当t∈(0，2]时，k＜恒成立，即k＜4t＋－15，因为4t＋≥12，当且仅当4t=，即t=时取等号，所以4t＋－15的最小值为－3.综上，实数k的取值范围为(－∞，－3)．
相关试卷
这是一份高考数学一轮复习作业本8.5 双曲线（含答案），共8页。
这是一份高考数学一轮复习作业本8.4 椭圆（含答案），共8页。
这是一份高考数学一轮复习作业本1.1 集合（含答案），共3页。
