


所属成套资源:高考数学一轮复习作业本 (含答案)
高考数学一轮复习作业本6.2 二元一次不等式(组)与简单的线性规划问题(含答案)
展开
这是一份高考数学一轮复习作业本6.2 二元一次不等式(组)与简单的线性规划问题(含答案),共9页。
2020高考数学(理数)复习作业本6.2 二元一次不等式(组)与简单的线性规划问题一 、选择题1.目标函数z=-2x+3y,将其看成直线方程时,z的意义是( )A.该直线的纵截距 B.该直线的纵截距的3倍C.该直线的横截距 D.该直线的横截距的3倍 2.变量x、y满足下列条件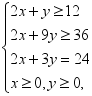 ,则使z=3x+2y最小的(x,y)是( )A.(4.5,3) B.(3,6) C.(9,2) D.(6,4) 3.已知a>0,x,y满足约束条件
,则使z=3x+2y最小的(x,y)是( )A.(4.5,3) B.(3,6) C.(9,2) D.(6,4) 3.已知a>0,x,y满足约束条件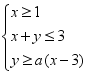 ,若z=2x+y的最小值为1,则a=( )A.
,若z=2x+y的最小值为1,则a=( )A.![]() B.
B.![]() C.1 D.2 4.某企业生产甲、乙两种产品,销售利润分别为2千元/件、1千元/件.甲、乙两种产品都需要在A,B两种设备上加工,生产一件甲产品需用A设备2小时,B设备6小时;生产一件乙产品需用A设备3小时,B设备1小时.A,B两种设备每月可使用时间数分别为480小时、960小时,若生产的产品都能及时售出,则该企业每月利润的最大值为( )A.320千元 B.360千元 C.400千元 D.440千元 5.某校今年计划招聘女教师a名,男教师b名.若a、b满足不等式组
C.1 D.2 4.某企业生产甲、乙两种产品,销售利润分别为2千元/件、1千元/件.甲、乙两种产品都需要在A,B两种设备上加工,生产一件甲产品需用A设备2小时,B设备6小时;生产一件乙产品需用A设备3小时,B设备1小时.A,B两种设备每月可使用时间数分别为480小时、960小时,若生产的产品都能及时售出,则该企业每月利润的最大值为( )A.320千元 B.360千元 C.400千元 D.440千元 5.某校今年计划招聘女教师a名,男教师b名.若a、b满足不等式组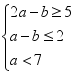 设这所学校今年计划招聘教师最多x名,则x=( )A.10 B.12 C.13 D.16 6.已知x,y满足约束条件
设这所学校今年计划招聘教师最多x名,则x=( )A.10 B.12 C.13 D.16 6.已知x,y满足约束条件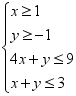 ,若目标函数z=y-mx(m>0)的最大值为1,则m的值是( )A.-
,若目标函数z=y-mx(m>0)的最大值为1,则m的值是( )A.-![]() B.1 C.2 D.5 7.已知实数x,y满足
B.1 C.2 D.5 7.已知实数x,y满足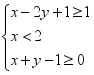 z=|2x-2y-1|,则z的取值范围是( )A.[
z=|2x-2y-1|,则z的取值范围是( )A.[![]() ,5] B.[0,5) C.[0,5] D.[
,5] B.[0,5) C.[0,5] D.[![]() ,5) 8.若实数x,y满足则z=的取值范围是( )A. B. C.[2,4] D.(2,4] 二 、填空题9.已知变量x,y满足
,5) 8.若实数x,y满足则z=的取值范围是( )A. B. C.[2,4] D.(2,4] 二 、填空题9.已知变量x,y满足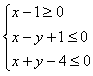 ,则
,则![]() 的最
的最![]() 小值是 。 10.设变量x、y满足约束条件
小值是 。 10.设变量x、y满足约束条件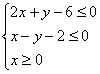 ,则目标函数z=2x-y的最大值为 . 11.若实数x,y满足不等式组
,则目标函数z=2x-y的最大值为 . 11.若实数x,y满足不等式组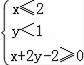 ,则
,则![]() 的取值范围是为 . 12.线性目标函数z=3x+2y,在线性约束条件
的取值范围是为 . 12.线性目标函数z=3x+2y,在线性约束条件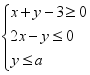 ,下取得最大值时的最优解只有一个,则实数a的取值范围是________. 三 、解答题13.设x,y满足约束条件
,下取得最大值时的最优解只有一个,则实数a的取值范围是________. 三 、解答题13.设x,y满足约束条件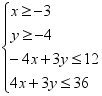 ,(1)求目标函数z=2x+3y的最小值与最大值;(2)求目标函数z=3x-y的最小值与最大值. 14.若x,y满足约束条件
,(1)求目标函数z=2x+3y的最小值与最大值;(2)求目标函数z=3x-y的最小值与最大值. 14.若x,y满足约束条件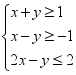 (1)求目标函数z=
(1)求目标函数z=![]() x-y+
x-y+![]() 的最值;(2)若目标函数z=ax+2y仅在点(1,0)处取得最小值,求a的取值范围. 15.某化肥厂生产甲、乙两种混合肥料,需要A,B,C三种主要原料.生产1车皮甲种肥料和生产1车皮乙种肥料所需三种原料的吨数如下表所示:原料肥料ABC甲483乙5510现有A种原料200吨,B种原料360吨,C种原料300吨,在此基础上生产甲、乙两种肥料.已知生产1车皮甲种肥料,产生的利润为2万元;生产1车皮乙种肥料,产生的利润为3万元.分别用x,y表示计划生产甲、乙两种肥料的车皮数.(1)用x,y列出满足生产条件的数学关系式,并画出相应的平面区域;(2)问分别生产甲、乙两种肥料各多少车皮能够产生最大的利润?并求出最大利润. 16.已知
的最值;(2)若目标函数z=ax+2y仅在点(1,0)处取得最小值,求a的取值范围. 15.某化肥厂生产甲、乙两种混合肥料,需要A,B,C三种主要原料.生产1车皮甲种肥料和生产1车皮乙种肥料所需三种原料的吨数如下表所示:原料肥料ABC甲483乙5510现有A种原料200吨,B种原料360吨,C种原料300吨,在此基础上生产甲、乙两种肥料.已知生产1车皮甲种肥料,产生的利润为2万元;生产1车皮乙种肥料,产生的利润为3万元.分别用x,y表示计划生产甲、乙两种肥料的车皮数.(1)用x,y列出满足生产条件的数学关系式,并画出相应的平面区域;(2)问分别生产甲、乙两种肥料各多少车皮能够产生最大的利润?并求出最大利润. 16.已知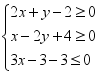 ,求z=|2x+y+5|的最大值与最小值.
,求z=|2x+y+5|的最大值与最小值.
答案解析1.答案为:B;2.答案为:B; 3.答案为:B;
 4.答案为:B.设生产甲产品x件,生产乙产品y件,利润为z千元,则z=2x+y,作出表示的可行域如图中阴影部分所示,作出直线2x+y=0,平移该直线,当直线z=2x+y经过直线2x+3y=480与直线6x+y=960的交点(150,60)(满足x∈N,y∈N)时,z取得最大值,为360.
4.答案为:B.设生产甲产品x件,生产乙产品y件,利润为z千元,则z=2x+y,作出表示的可行域如图中阴影部分所示,作出直线2x+y=0,平移该直线,当直线z=2x+y经过直线2x+3y=480与直线6x+y=960的交点(150,60)(满足x∈N,y∈N)时,z取得最大值,为360.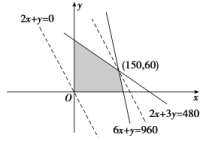 5.答案为:C;解析:如图所示,画出约束条件所表示的区域,即可行域,作直线b+a=0,并平移,结合a,b∈N,可知当a=6,b=7时,a+b取最大值,故x=6+7=13.
5.答案为:C;解析:如图所示,画出约束条件所表示的区域,即可行域,作直线b+a=0,并平移,结合a,b∈N,可知当a=6,b=7时,a+b取最大值,故x=6+7=13.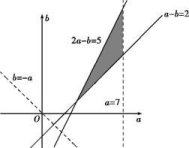 6.答案为:B;解析:作出可行域,如图所示的阴影部分.∵m>0,∴当直线z=y-mx经过点A时,z取最大值,解得x=1,y=2即A(1,2),∴2-m=1,解得m=1.故选B.
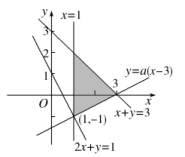
6.答案为:B;解析:作出可行域,如图所示的阴影部分.∵m>0,∴当直线z=y-mx经过点A时,z取最大值,解得x=1,y=2即A(1,2),∴2-m=1,解得m=1.故选B.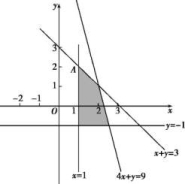 7.答案为:B;解析:作出可行域如图所示:易求得A(2,1.5),B(
7.答案为:B;解析:作出可行域如图所示:易求得A(2,1.5),B(![]() ,
,![]() ),C(2,-1),令μ=2x-2y-1,则y=x-
),C(2,-1),令μ=2x-2y-1,则y=x-![]() ,当直线y=x-
,当直线y=x-![]() 过点C(2,-1)时,μ有最大值5,过点B(
过点C(2,-1)时,μ有最大值5,过点B(![]() ,
,![]() )时,μ有最小值-
)时,μ有最小值-![]() ,因为可行域不包括直线x=2,所以z=|2x-2y-1|的取值范围是[0,5).故选B.
,因为可行域不包括直线x=2,所以z=|2x-2y-1|的取值范围是[0,5).故选B. 8.答案为:B.作出不等式组对应的平面区域如图中阴影部分(不包括边界OB)所示,其中A(1,2),B(0,2).z===,
8.答案为:B.作出不等式组对应的平面区域如图中阴影部分(不包括边界OB)所示,其中A(1,2),B(0,2).z===,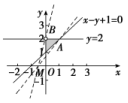 则z的几何意义是可行域内的点P(x,y)与点M所连直线的斜率.可知kMA==,kMB==4,结合图形可得≤z<4.故z=的取值范围是. 一 、填空题9.答案为:0.25.10.答案为:
则z的几何意义是可行域内的点P(x,y)与点M所连直线的斜率.可知kMA==,kMB==4,结合图形可得≤z<4.故z=的取值范围是. 一 、填空题9.答案为:0.25.10.答案为:![]() ; 11.答案为:[4/3,3].
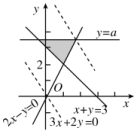
; 11.答案为:[4/3,3].  12.答案为:[2,+∞);
12.答案为:[2,+∞);
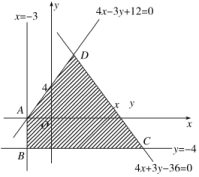
 二 、解答题13.解:
二 、解答题13.解:
 14.解:(1)作出可行域如图,可求得A(3,4),B(0,1),C(1,0).由图可知当目标函数线过A(3,4)时z取最小值-2,过C(1,0)时z取最大值1.所以z的最大值为1,最小值为-2.
14.解:(1)作出可行域如图,可求得A(3,4),B(0,1),C(1,0).由图可知当目标函数线过A(3,4)时z取最小值-2,过C(1,0)时z取最大值1.所以z的最大值为1,最小值为-2.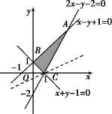 (2)由图可知-1<-
(2)由图可知-1<-![]() <2,解得-4<a<2.故所求a的取值范围为(-4,2). 15.解:(1)由已知,x,y满足的数学关系式为
<2,解得-4<a<2.故所求a的取值范围为(-4,2). 15.解:(1)由已知,x,y满足的数学关系式为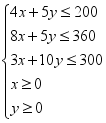 ,解析:该二元一次不等式组所表示的平面区域为图1中的阴影部分:(2)设利润为z万元,则目标函数为z=2x+3y.考虑z=2x+3y,将它变形为y=-
,解析:该二元一次不等式组所表示的平面区域为图1中的阴影部分:(2)设利润为z万元,则目标函数为z=2x+3y.考虑z=2x+3y,将它变形为y=-![]() x+
x+![]() ,这是斜率为-
,这是斜率为-![]() ,随z变化的一族平行直线.
,随z变化的一族平行直线.![]() 为直线在y轴上的截距,当
为直线在y轴上的截距,当![]() 取最大值时,z的值最大.又因为x,y满足约束条件,所以由图2可知,当直线z=2x+3y经过可行域上的点M时,截距
取最大值时,z的值最大.又因为x,y满足约束条件,所以由图2可知,当直线z=2x+3y经过可行域上的点M时,截距![]() 最大,即z最大.解方程组
最大,即z最大.解方程组![]() 得点M的坐标为(20,24).所以zmax=2×20+3×24=112.答:生产甲种肥料20车皮、乙种肥料24车皮时利润最大,且最大利润为112万元.
得点M的坐标为(20,24).所以zmax=2×20+3×24=112.答:生产甲种肥料20车皮、乙种肥料24车皮时利润最大,且最大利润为112万元.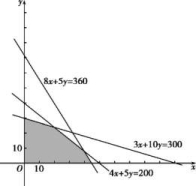
 16.解:
16.解:
相关试卷
这是一份高考数学(文数)一轮复习创新思维课时练6.2《二元一次不等式(组)与简单的线性规划问题》(教师版),共9页。
这是一份高考数学(文数)一轮复习课时练习:6.2《二元一次不等式(组)与简单的线性规划问题》(教师版),共10页。试卷主要包含了已知变量x,y满足,若实数x,y满足等内容,欢迎下载使用。
这是一份高考数学(理数)一轮复习检测卷:6.2《二元一次不等式(组)与简单的线性规划问题》 (学生版),共3页。










