高考数学一轮复习作业本6.4 不等式有关证明（含答案）

这是一份高考数学一轮复习作业本6.4 不等式有关证明（含答案），共7页。
2020高考数学(理数)复习作业本6.4 不等式有关证明一         、选择题1.设a>b>1,c<0,给出下列三个结论:①>;②ac<bc;③logb(a-c)>loga(b-c).其中所有的正确结论的序号是(　   　)A.①                                   B.①②                                    C.②③                                    D.①②③ 2.设a，b，c均为正实数，则三个数a＋，b＋，c＋(　　)A．都大于2　　                    B．都小于2C．至少有一个不大于2              D．至少有一个不小于2 3.在等比数列{an}中，a1＜a2＜a3是数列{an}递增的(　　)A．充分不必要条件 B．必要不充分条件C．充要条件D．既不充分也不必要条件 4.设m=(x+2)(x+3),n=2x2+5x+9,则m与n的大小关系为(　  　)A.m>n                                      B.m<n                                          C.m≥n                                         D.m≤n 5.若m<0,n>0且m+n<0,则下列不等式成立的是(　    　)A.-n<m<n<-m                  B.-n<m<-m<n        C.m<-n<-m<n                      D.m<-n<n<-m 6.设{an}是等差数列，下列结论中正确的是(　　)A．若a1＋a2＞0，则a2＋a3＞0B．若a1＋a3＜0，则a1＋a2＜0C．若0＜a1＜a2，则a2＞D．若a1＜0，则(a2－a1)(a2－a3)＞0 7.设集合A={(x，y)|x－y≥1，ax＋y＞4，x－ay≤2}，则(　　)A．对任意实数a，(2，1)∈AB．对任意实数a，(2，1)∉AC．当且仅当a＜0时，(2，1)∉AD．当且仅当a≤1.5时，(2，1)∉A 8.已知两个半径不等的圆盘叠放在一起(有一轴穿过它们的圆心)，两圆盘上分别有互相垂直的两条直径将其分为四个区域，小圆盘上所写的实数分别记为x1，x2，x3，x4，大圆盘上所写的实数分别记为y1，y2，y3，y4，如图所示．将小圆盘逆时针旋转i(i=1，2，3，4)次，每次转动90°，记Ti(i=1，2，3，4)为转动i次后各区域内两数乘积之积，例如T1=x1y2＋x2y3＋x3y4＋x4y1.若x1＋x2＋x3＋x4＜0，y1＋y2＋y3＋y4＜0，则以下结论正确的是(　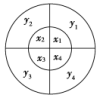　)A．T1，T2，T3，T4中至少有一个为正数B．T1，T2，T3，T4中至少有一个为负数C．T1，T2，T3，T4中至多有一个为正数D．T1，T2，T3，T4中至多有一个为负数 二         、填空题9.已知a，b是不相等的正数，x=，y=，则x、y的大小关系是________． 10.给出下列条件：①1＜a＜b；②0＜a＜b＜1；③0＜a＜1＜b.其中，能推出logb＜loga＜logab成立的条件的序号是________(填上所有可能的条件的序号)． 11.设实数x,y满足3≤xy2≤8,4≤≤9,则的最大值为　　　　.  12.在R上定义运算⊙：x⊙y=x(2－y)，若不等式(x＋m)⊙x＜1对一切实数x恒成立，则实数m的取值范围是________． 三         、解答题13.已知a≠0,b≠0,且a+b>0,试比较+与+的大小.      14. (1)当x＞1时，求证：2x2＋＞2x＋＞2＋；(2)若a＜e，用反证法证明：函数f(x)=xex－ax2(x＞0)无零点．           15. (1)设x≥1，y≥1，证明：x＋y＋≤＋＋xy；(2)1＜a≤b≤c，证明：logab＋logbc＋logca≤logba＋logcb＋logac.               16.已知数列{an}的各项均为正数，bn=nan(n∈N*)，e为自然对数的底数．(1)求函数f(x)=1＋x－ex的单调区间，并比较与e的大小；(2)计算，，，由此推测计算的公式，并给出证明．               
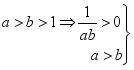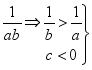答案解析1.答案为：D；解析：①⇒a·>b·⇒<⇒>,∴①正确;②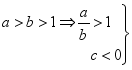⇒⇒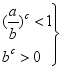ac<bc,∴②正确;③⇒⇒⇒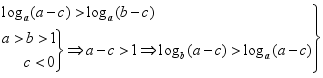logb(a-c)>loga(b-c),∴③正确.故选D.2.答案为：D.解析：因为a＞0，b＞0，c＞0，所以＋＋=＋＋≥6，当且仅当a=b=c时，等号成立，故三者不能都小于2，即至少有一个不小于2.  3.答案为：C.解析：当a1＜a2＜a3时，设公比为q，由a1＜a1q＜a1q2得若a1＞0，则1＜q＜q2，即q＞1，此时，显然数列{an}是递增数列，若a1＜0，则1＞q＞q2，即0＜q＜1，此时，数列{an}也是递增数列，反之，当数列{an}是递增数列时，显然a1＜a2＜a3.故a1＜a2＜a3是等比数列{an}递增的充要条件．  4.答案为：B；解析：m-n=x2+5x+6-(2x2+5x+9)=-x2-3<0,∴m<n.故选B.5.答案为：D；解析：解法一:(取特殊值法)令m=-3,n=2,分别对各选项进行检验即可.解法二:m+n<0⇒又由于m<0<n,故m<-n<n<-m成立.6.答案为：C.解析：设等差数列{an}的公差为d，若a1＋a2＞0，a2＋a3=a1＋d＋a2＋d=(a1＋a2)＋2d，由于d正负不能确定，因而a2＋a3符号不确定，故选项A错误；若a1＋a3＜0，a1＋a2=a1＋a3－d=(a1＋a3)－d，由于d正负不能确定，因而a1＋a2符号不确定，故选项B错误；若0＜a1＜a2，可知a1＞0，d＞0，a2＞0，a3＞0，∴a－a1a3=(a1＋d)2－a1(a1＋2d)=d2＞0，∴a2＞，故选项C正确；若a1＜0，则(a2－a1)(a2－a3)=d·(－d)=－d2≤0，故选项D错，故选C.  7.答案为：D.解析：若点(2，1)∈A，则不等式x－y≥1显然成立．且满足解得a＞1.5.即点(2，1)∈A⇒a＞1.5，其等价命题为a≤1.5⇒点(2，1)∉A成立．  8.答案为：A.根据题意可知：(x1＋x2＋x3＋x4)(y1＋y2＋y3＋y4)＞0，又(x1＋x2＋x3＋x4)(y1＋y2＋y3＋y4)去掉括号即得：(x1＋x2＋x3＋x4)·(y1＋y2＋y3＋y4)=T1＋T2＋T3＋T4＞0，所以可知T1，T2，T3，T4中至少有一个为正数，故选A.   一         、填空题9.答案为：y＞x；解析：x2=(a＋b＋2)，y2=a＋b=(a＋b＋a＋b)＞(a＋b＋2)=x2，又∵x＞0，y＞0，∴y＞x.  10.答案为：②；解析：若1＜a＜b，则＜＜1＜b，所以loga＜loga=－1=logb，故条件①不成立；若0＜a＜b＜1，则b＜1＜＜，所以logab＞loga＞loga=－1=logb，故条件②成立；若0＜a＜1＜b，则0＜＜1，所以loga＞0，logab＜0，故条件③不成立．  11.答案为：27；解析：设=(xy2)m·=xm+2ny2m-n.则解得∴=·,由4≤≤9,3≤xy2≤8,得16≤≤81,≤≤,∴2≤≤27.故的最大值为27.12.答案为：(－4，0)；解析：由题意得不等式(x＋m)(2－x)＜1，即x2＋(m－2)x＋(1－2m)＞0对任意x∈R恒成立，因此Δ=(m－2)2－4(1－2m)＜0，即m2＋4m＜0，解得－4＜m＜0.   二         、解答题13.解：.∵a+b>0,(a-b)2≥0,a2b2>0,∴≥0.∴+≥+.14.证明：(1)∵x＞1，∴要证2x2＋＞2x＋，只需证2x4＋1＞2x3＋x，即证2x3(x－1)＞x－1.∵x＞1，∴只需证2x3＞1.∵x＞1，∴2x3＞2＞1，故2x2＋＞2x＋得证．令x=，则2()2＋＞2＋，即2t＋＞2＋，则2x＋＞2＋，从而2x2＋＞2x＋＞2＋.(2)假设函数f(x)=xex－ax2(x＞0)有零点，则f(x)=0在(0，＋∞)上有解，即a=在(0，＋∞)上有解．设g(x)=(x＞0)，则导函数g′(x)=(x＞0)，当0＜x＜1时，g′(x)＜0；当x＞1时，g′(x)＞0.∴g(x)≥g(x)min=g(1)=e，∴a≥e，但这与条件a＜e矛盾，故假设不成立，即原命题得证．  15.证明：(1)由于x≥1，y≥1，所以要证明x＋y＋≤＋＋xy，只要证明xy(x＋y)＋1≤y＋x＋(xy)2，只要证明(xy)2－1＋(x＋y)－xy(x＋y)≥0，只要证明(xy－1)(xy＋1－x－y)≥0，只要证明(xy－1)(x－1)(y－1)≥0.由于x≥1，y≥1，上式显然成立，所以原命题成立．(2)设logab=x，logbc=y，则logca==，logba=，logcb=，logac=xy，所以要证明不等式logab＋logbc＋logca≤logba＋logcb＋logac，即证x＋y＋≤＋＋xy.因为c≥b≥a＞1，所以x=logab≥1，y=logbc≥1，由(1)知所要证明的不等式成立．  16.解：(1)f(x)的定义域为(－∞，＋∞)，f′(x)=1－ex.当f′(x)＞0，即x＜0时，f(x)单调递增；当f′(x)＜0，即x＞0时，f(x)单调递减．故f(x)的单调递增区间为(－∞，0)，单调递减区间为(0，＋∞)．当x＞0时，f(x)＜f(0)=0，即1＋x＜ex.令x=，得1＋＜e，即＜e.①(2)=1·=1＋1=2；=·=2·2=(2＋1)2=32；=·=32·3=(3＋1)3=43.由此推测：=(n＋1)n.②下面用数学归纳法证明②.(ⅰ)当n=1时，左边=右边=2，②式成立．(ⅱ)假设当n=k时，②式成立，即=(k＋1)k.当n=k＋1时，bk＋1=(k＋1)ak＋1，由归纳假设可得=·=(k＋1)k(k＋1)=(k＋2)k＋1.所以当n=k＋1时，②式也成立．根据(ⅰ)(ⅱ)，可知②式对一切正整数n都成立．