


所属成套资源:高考数学一轮复习作业本 (含答案)
高考数学一轮复习作业本8.5 双曲线(含答案)
展开
这是一份高考数学一轮复习作业本8.5 双曲线(含答案),共8页。
2020高考数学(理数)复习作业本8.5 双曲线一 、选择题1.已知双曲线方程为![]() ,过P(1,0)的直线l与双曲线只有一个公共点,则共有( )A.4条 B.3条 C.2条 D.1条 2.双曲线C:
,过P(1,0)的直线l与双曲线只有一个公共点,则共有( )A.4条 B.3条 C.2条 D.1条 2.双曲线C:![]() (a>0,b>0)的离心率为2,焦点到渐近线的距离为,则双曲线C的焦距等于( ) A.2 B.2 C.4 D.4 3.方程
(a>0,b>0)的离心率为2,焦点到渐近线的距离为,则双曲线C的焦距等于( ) A.2 B.2 C.4 D.4 3.方程![]() 表示双曲线,则m的取值范围为( )A.-2<m<2 B.m>0 C.m≥0 D.|m|≥2 4.设动点P到A(-5,0)的距离与它到B(5,0)距离的差等于6,则P点的轨迹方程是( )A.
表示双曲线,则m的取值范围为( )A.-2<m<2 B.m>0 C.m≥0 D.|m|≥2 4.设动点P到A(-5,0)的距离与它到B(5,0)距离的差等于6,则P点的轨迹方程是( )A.![]() B.
B.![]() C.
C.![]() (x≤-3) D.
(x≤-3) D.![]() (x≥3) 5.已知双曲线E:
(x≥3) 5.已知双曲线E:![]() 的渐近线相互垂直,则E的离心率为( )A.
的渐近线相互垂直,则E的离心率为( )A.![]() B.
B.![]() C.2 D.
C.2 D.![]() 6.已知点P,A,B在双曲线-=1(a>0,b>0)上,直线AB过坐标原点,且直线PA,PB的斜率之积为,则双曲线的离心率为( )A. B. C.2 D. 7.已知双曲线E:-=1(a>0,b>0)的左、右焦点分别为F1,F2,|F1F2|=6,P是双曲线E右支上一点,PF1与y轴交于点A,△PAF2的内切圆与AF2相切于点Q.若|AQ|=,则双曲线E的离心率是( )A.2 B. C. D. 8.已知双曲线C:-=1(a>0,b>0)的焦距为2c,直线l过点且与双曲线C的一条渐近线垂直,以双曲线C的右焦点为圆心,半焦距为半径的圆Ω与直线l交于M,N两点,若|MN|=c,则双曲线C的渐近线方程为( )A.y=±x B.y=±x C.y=±2x D.y=±4x 二 、填空题9.设F1,F2分别为双曲线C:-=1(a>0,b>0)的两个焦点,M,N是双曲线C的一条渐近线上的两点,四边形MF1NF2为矩形,A为双曲线的一个顶点,若△AMN的面积为c2,则该双曲线的离心率为________. 10.双曲线
6.已知点P,A,B在双曲线-=1(a>0,b>0)上,直线AB过坐标原点,且直线PA,PB的斜率之积为,则双曲线的离心率为( )A. B. C.2 D. 7.已知双曲线E:-=1(a>0,b>0)的左、右焦点分别为F1,F2,|F1F2|=6,P是双曲线E右支上一点,PF1与y轴交于点A,△PAF2的内切圆与AF2相切于点Q.若|AQ|=,则双曲线E的离心率是( )A.2 B. C. D. 8.已知双曲线C:-=1(a>0,b>0)的焦距为2c,直线l过点且与双曲线C的一条渐近线垂直,以双曲线C的右焦点为圆心,半焦距为半径的圆Ω与直线l交于M,N两点,若|MN|=c,则双曲线C的渐近线方程为( )A.y=±x B.y=±x C.y=±2x D.y=±4x 二 、填空题9.设F1,F2分别为双曲线C:-=1(a>0,b>0)的两个焦点,M,N是双曲线C的一条渐近线上的两点,四边形MF1NF2为矩形,A为双曲线的一个顶点,若△AMN的面积为c2,则该双曲线的离心率为________. 10.双曲线![]() 的渐近线方程为 . 11.过双曲线
的渐近线方程为 . 11.过双曲线![]() 的左焦点F1,作倾斜角为的直线AB,其中A,B分别为直线与双曲线的交点,则|AB|的长为________. 12.已知双曲线-=1,过双曲线的上焦点F1作圆O:x2+y2=25的一条切线,切点为M,交双曲线的下支于点N,T为NF1的中点,则△MOT的外接圆的周长为________. 三 、解答题13.双曲线与椭圆
的左焦点F1,作倾斜角为的直线AB,其中A,B分别为直线与双曲线的交点,则|AB|的长为________. 12.已知双曲线-=1,过双曲线的上焦点F1作圆O:x2+y2=25的一条切线,切点为M,交双曲线的下支于点N,T为NF1的中点,则△MOT的外接圆的周长为________. 三 、解答题13.双曲线与椭圆![]() 有相同的焦点,它的一条渐近线为y=x,求双曲线的标准方程和离心率. 14.已知双曲线
有相同的焦点,它的一条渐近线为y=x,求双曲线的标准方程和离心率. 14.已知双曲线![]() 的右焦点为(2,0).(1)求双曲线的方程;(2)求双曲线的渐近线与直线x=-2围成的三角形的面积. 15.已知中心在原点的双曲线C的右焦点为(2,0),右顶点为(
的右焦点为(2,0).(1)求双曲线的方程;(2)求双曲线的渐近线与直线x=-2围成的三角形的面积. 15.已知中心在原点的双曲线C的右焦点为(2,0),右顶点为(![]() ,0).(1)求双曲线C的方程; (2)若直线l:y=kx+
,0).(1)求双曲线C的方程; (2)若直线l:y=kx+![]() 与双曲线C恒有两个不同的交点A和B,且·>2,其中O为原点,求k的取值范围. 16.如图,椭圆E的左右顶点分别为A、B,左右焦点分别为F1、F2,
与双曲线C恒有两个不同的交点A和B,且·>2,其中O为原点,求k的取值范围. 16.如图,椭圆E的左右顶点分别为A、B,左右焦点分别为F1、F2,![]() ,直线y=kx+m(k>0)交椭圆于C、D两点,与线段F1F2及椭圆短轴分别交于M,N两点(M,N不重合),且|CM|=|DN|.(1)求椭圆E的离心率;(2)若m>0,设直线AD、BC的斜率分别为
,直线y=kx+m(k>0)交椭圆于C、D两点,与线段F1F2及椭圆短轴分别交于M,N两点(M,N不重合),且|CM|=|DN|.(1)求椭圆E的离心率;(2)若m>0,设直线AD、BC的斜率分别为![]() ,求
,求![]() 的取值范围.
的取值范围.
答案解析1.答案为:B; 2.答案为:C;
2.答案为:C;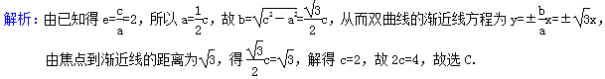 3.答案为:A;解析:∵已知方程表示双曲线,∴(2+m)(2-m)>0.∴-2<m<2.4.答案为:D;
3.答案为:A;解析:∵已知方程表示双曲线,∴(2+m)(2-m)>0.∴-2<m<2.4.答案为:D;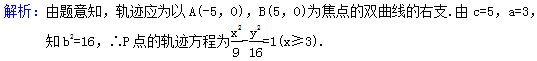 5.A.6.答案为:A.解析:根据双曲线的对称性可知点A,B关于原点对称,设A(x1,y1),B(-x1,-y1),P(x,y),所以-=1,-=1,两式相减得=,即=,因为直线PA,PB的斜率之积为,所以kPA·kPB=·===,所以双曲线的离心率为e===.故选A.7.答案为:C.如图,设△PAF2的内切圆与PF2相切于点M.依题意知,|AF1|=|AF2|,根据双曲线的定义,以及P是双曲线E右支上一点,得2a=|PF1|-|PF2|,根据三角形内切圆的性质,得|PF1|=|AF1|+|PA|=|AF1|+(|PM|+|AQ|),|PF2|=|PM|+|MF2|=|PM|+|QF2|=|PM|+(|AF2|-|AQ|).所以2a=2|AO|=2,即a=.因为|F1F2|=6,所以c=3,所以双曲线E的离心率是e===,故选C.
5.A.6.答案为:A.解析:根据双曲线的对称性可知点A,B关于原点对称,设A(x1,y1),B(-x1,-y1),P(x,y),所以-=1,-=1,两式相减得=,即=,因为直线PA,PB的斜率之积为,所以kPA·kPB=·===,所以双曲线的离心率为e===.故选A.7.答案为:C.如图,设△PAF2的内切圆与PF2相切于点M.依题意知,|AF1|=|AF2|,根据双曲线的定义,以及P是双曲线E右支上一点,得2a=|PF1|-|PF2|,根据三角形内切圆的性质,得|PF1|=|AF1|+|PA|=|AF1|+(|PM|+|AQ|),|PF2|=|PM|+|MF2|=|PM|+|QF2|=|PM|+(|AF2|-|AQ|).所以2a=2|AO|=2,即a=.因为|F1F2|=6,所以c=3,所以双曲线E的离心率是e===,故选C. 8.答案为:B.解析:由题意得,双曲线的渐近线方程为y=±x,设垂直于直线l的渐近线方程为y=x,则直线l的斜率k1=-,直线l的方程为y=-,整理可得,ax+by-a2=0,焦点(c,0)到直线l的距离d==,则|MN|=2=2=c,整理可得c4-9a2c2+12a3c-4a4=0,即e4-9e2+12e-4=0,即(e-1)(e-2)(e2+3e-2)=0,又双曲线的离心率e>1,所以e==2,所以b=a,故双曲线C的渐近线方程为y=±x,故选B. 9.答案为:;解析:设M,根据矩形的性质,得|MO|=|OF1|=|OF2|=c,即x2+=c2,则x=a,所以M(a,b).因为△AMN的面积为c2,所以2××a×b=c2,所以4a2(c2-a2)=c4,所以e4-4e2+4=0,所以e=.10.答案为:y=±
8.答案为:B.解析:由题意得,双曲线的渐近线方程为y=±x,设垂直于直线l的渐近线方程为y=x,则直线l的斜率k1=-,直线l的方程为y=-,整理可得,ax+by-a2=0,焦点(c,0)到直线l的距离d==,则|MN|=2=2=c,整理可得c4-9a2c2+12a3c-4a4=0,即e4-9e2+12e-4=0,即(e-1)(e-2)(e2+3e-2)=0,又双曲线的离心率e>1,所以e==2,所以b=a,故双曲线C的渐近线方程为y=±x,故选B. 9.答案为:;解析:设M,根据矩形的性质,得|MO|=|OF1|=|OF2|=c,即x2+=c2,则x=a,所以M(a,b).因为△AMN的面积为c2,所以2××a×b=c2,所以4a2(c2-a2)=c4,所以e4-4e2+4=0,所以e=.10.答案为:y=±![]() x. 11.答案为:3;
x. 11.答案为:3; 12.答案为:π;解析:如图,∵F1M为圆的切线,∴OM⊥F1M,在直角三角形OMF1中,|OM|=5.设双曲线的下焦点为F2,连接NF2,∴OT为△F1F2N的中位线,∴2|OT|=|NF2|.设|OT|=x,则|NF2|=2x,又|NF1|-|NF2|=10,∴|NF1|=|NF2|+10=2x+10,∴|TF1|=x+5.由勾股定理得|F1M|2=|OF1|2-|OM|2=132-52=144,|F1M|=12,∴|MT|=|x-7|,在直角三角形OMT中,|OT|2-|MT|2=|OM|2,即x2-(x-7)2=52,∴x=.又△OMT是直角三角形,故其外接圆的直径为|OT|=,∴△MOT的外接圆的周长为π.
12.答案为:π;解析:如图,∵F1M为圆的切线,∴OM⊥F1M,在直角三角形OMF1中,|OM|=5.设双曲线的下焦点为F2,连接NF2,∴OT为△F1F2N的中位线,∴2|OT|=|NF2|.设|OT|=x,则|NF2|=2x,又|NF1|-|NF2|=10,∴|NF1|=|NF2|+10=2x+10,∴|TF1|=x+5.由勾股定理得|F1M|2=|OF1|2-|OM|2=132-52=144,|F1M|=12,∴|MT|=|x-7|,在直角三角形OMT中,|OT|2-|MT|2=|OM|2,即x2-(x-7)2=52,∴x=.又△OMT是直角三角形,故其外接圆的直径为|OT|=,∴△MOT的外接圆的周长为π.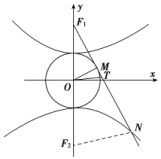 13.解:
13.解: 14.解:
14.解: 15.解:
15.解: 16.解:
16.解:
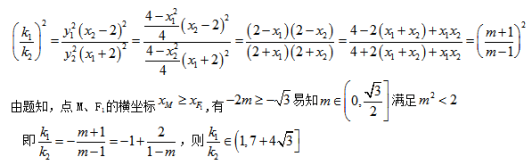
相关试卷
这是一份(新高考)高考数学一轮考点复习8.5《双曲线》课时跟踪检测(含详解),共9页。试卷主要包含了基础练——练手感熟练度,综合练——练思维敏锐度,自选练——练高考区分度等内容,欢迎下载使用。
这是一份高考数学(理数)一轮复习检测卷:8.5《双曲线》 (学生版),共3页。试卷主要包含了当双曲线M,已知F是双曲线C,已知双曲线C,设F1,F2分别为双曲线C等内容,欢迎下载使用。
这是一份高考数学(理数)一轮复习检测卷:8.5《双曲线》 (教师版)










