高考数学一轮复习考点测试刷题本18 任意角 弧度制 任意角的三角函数（含答案解析）

2020高考数学(文数)考点测试刷题本18

任意角 弧度制 任意角的三角函数

一         、选择题

1.一个扇形的弧长与面积的数值都是6，则这个扇形的圆心角的弧度数是(　　)

A．1             B．2           C．3             D．4

2.已知扇形的周长为8cm，圆心角为2弧度，则该扇形的面积为(        )

A.4cm2       B.6cm2        C.8cm2         D.16cm2

3.时钟的分针经过15分钟旋转的角为(　　)

A.15°　　B.90°　　C.-15°　　D.-90°

4.在平面直角坐标系中，点M(3，m)在角α的终边上，点N(2m，4)在角α＋的终边上，则m=(　　)

A．－6或1         B．－1或6        C．6         D．1

5.已知sinθ－cosθ>1，则角θ的终边在(　　)

A．第一象限        B．第二象限       C．第三象限       D．第四象限

6.已知角α终边上一点P的坐标是(2sin 2，－2cos 2)，则sin α等于(　　)

A．sin 2         B．－sin 2       C．cos 2          D．－cos 2

7.若sinθ,cosθ是方程4x2+2mx+m=0的两根，则m的值为（     ）

  A.                                  B.                                     C.                                     D.

8.已知角α=2kπ－(k∈Z)，若角θ与角α的终边相同，则y=＋＋的值为(　　)

A．1             B．－1           C．3             D．－3

二         、填空题

9.弧长为3π，圆心角为135°的扇形半径为__________.

10.若角α的终边经过点P(1,-2)，则sinα的值为______________.

11.已知，，那么cosθ-sinθ的值是            .

12.已知角α的终边经过点(3a－9，a＋2)，且cos α≤0，sin α>0，则实数a的取值范围是________．

三         、解答题

13.已知一扇形的圆心角是α，所在圆的半径是R.

(1)若α=60°，R=10 cm，求扇形的弧长及该弧所在的弓形面积；

(2)若扇形的周长是一定值C(C>0)，当α为多少弧度时，该扇形有最大面积？

14.已知角α的顶点与原点O重合，始边与x轴的非负半轴重合，它的终边过点P(－，－).

(1)求sin(α＋π)的值；

(2)若角β满足sin(α＋β)=，求cosβ的值．

15.如图，在平面直角坐标系xOy中，角α的始边与x轴的非负半轴重合且与单位圆相交于A点，它的终边与单位圆相交于x轴上方一点B，始边不动，终边在运动．

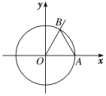
(1)若点B的横坐标为－，求tan α的值；

(2)若△AOB为等边三角形，写出与角α终边相同的角β的集合；

(3)若α∈，请写出弓形AB的面积S与α的函数关系式．

16.在平面直角坐标系xOy中，角α的顶点是坐标原点，始边为x轴的正半轴，终边与单位圆O交于点A(x1，y1)，α∈.将角α终边绕原点按逆时针方向旋转，交单位圆于点B(x2，y2)．

(1)若x1=，求x2；

(2)过A，B作x轴的垂线，垂足分别为C，D，记△AOC及△BOD的面积分别为S1，S2，且S1=S2，求tanα的值．

答案解析

1.答案为：C；

2.答案为：A

4.答案为：A；

解析：由题意得，tanα=，tanα＋==，∴=，∴m=－6或1，故选A.

5.答案为：B；

解析：

由已知得(sinθ－cosθ)2>1，即1－2sinθcosθ>1，sinθcosθ<0，

又sinθ>cosθ，所以sinθ>0>cosθ，所以角θ的终边在第二象限．故选B.

6.答案为：D；

7.答案为：B.

8.答案为：B；

解析：由α=2kπ－(k∈Z)及终边相同的概念知，角α的终边在第四象限，

又角θ与角α的终边相同，所以角θ是第四象限角，

所以sin θ＜0，cos θ＞0，tan θ＜0.所以y=－1＋1－1=－1.

9.答案为：4.

10.答案为：;  

11.答案为：;

12.答案为：(－2,3]；

解析：∵cos α≤0，sin α>0，∴角α的终边落在第二象限或y轴的正半轴上．

∴∴－2<a≤3.

13.解：

14.解：

(1)由角α的终边过点P－，－得sinα=－，所以sin(α＋π)=－sinα=.

(2)由角α的终边过点P－，－，得cosα=－，

由sin(α＋β)=得cos(α＋β)=±.

由β=(α＋β)－α得cosβ=cos(α＋β)cosα＋sin(α＋β)sinα，

所以cosβ=－或cosβ=.

15.解：

(1)由题意可得B，根据三角函数的定义得tan α==－.

(2)若△AOB为等边三角形，则B，可得tan∠AOB==，故∠AOB=；

故与角α终边相同的角β的集合为β|β=＋2kπ，k∈Z.

(3)若α∈，则S扇形OAB=αr2=α，

而S△AOB=×1×1×sin α=sin α，

故弓形AB的面积S=S扇形OAB－S△AOB=α－sin α，α∈.

16.解：

(1)因为x1=，y1>0，所以y1==，所以sinα=，cosα=，

所以x2=cos=cosαcos－sinαsin=－.

(2)S1=sinαcosα=sin2α.因为α∈，所以α＋∈，

所以S2=－sincos=－sin=－cos2α.

因为S1=S2，所以sin2α=－cos2α，即tan2α=－，

所以=－，解得tanα=2或tanα=－.

因为α∈，所以tanα=2.