高考数学一轮复习考点测试刷题本21 函数y＝A(sinωx＋φ)+b的图象与性质（含答案解析）

2020高考数学(文数)考点测试刷题本21

函数y＝A(sinωx＋φ)+b的图象与性质

一         、选择题

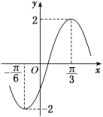
1.函数f(x)=Acos(ωx＋φ)(A>0，ω>0，－π<φ<0)的部分图象如图所示，为了得到g(x)=Asin ωx的图象，只需将函数y=f(x)的图象(　　)

A．向左平移个单位长度       B．向左平移个单位长度

C．向右平移个单位长度       D．向右平移个单位长度

2.将函数f(x)=tan(0<ω<10)的图象向右平移个单位长度之后与函数f(x)的图象重合，则ω=(　　)

A．9            B．6           C．4            D．8

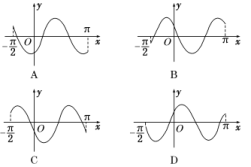
3.将函数y=sin的图象向右平移个单位长度，所得图象对应的函数(　　)

A．在区间上单调递增       B．在区间上单调递减

C．在区间上单调递增       D．在区间上单调递减

4.函数y=sin在区间上的简图是(　　)

5.将函数y=f(x)=2sin的图象向左平移个单位长度，再把所有点的横坐标缩短到原来的，纵坐标不变，得到函数y=g(x)的图象，则下面对函数y=g(x)的叙述正确的是(　　)

A．函数g(x)=2sin

B．函数g(x)的周期为π

C．函数g(x)的一个对称中心为点

D．函数g(x)在区间上单调递增

6.若将函数y=2sin 2x的图象向左平移个单位长度，则平移后图象的对称轴为(　　)

A．x=－(k∈Z)   B．x=＋(k∈Z)   C．x=－(k∈Z) D．x=＋(k∈Z)

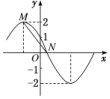
7.已知函数f(x)=2sin(ωx＋φ)ω>0，φ∈的部分图象如图所示，其中f(0)=1，|MN|=，将f(x)的图象向右平移1个单位长度，得到函数g(x)的图象，则g(x)的解析式是(　　)

A．g(x)=2cos x                 B．g(x)=2sin

C．g(x)=2sin           D．g(x)=－2cos x

8.方程sinx=lgx的实根有（    ）

A.1个         B.3个         C.2个      D.无穷多个

二         、填空题

9.据市场调查，某种商品一年内每件出厂价在7千元的基础上，按月呈f(x)=Asin(ωx＋φ)＋B

(A>0，ω>0，|φ|<)的模型波动(x为月份)，已知3月份达到最高价9千元，9月份价格最低为5千元．则7月份的出厂价格为________元．

10.已知角φ的终边经过点P(－4，3)，函数f(x)=sin(ωx＋φ)(ω＞0)的图象的相邻两条对称轴之间的距离等于，则f的值为________．

11.要得到 y=sin2x-cos2x 的图象，只需将函数 y=sin2x+cos2x 的图象沿x轴向____移___________个单位.

12.已知函数f(x)=sin(ωx＋φ)的图象上的一个最高点和与它相邻的一个最低点的距离为2，且图象过点，则函数f(x)=____________.

三         、解答题

13.已知函数f(x)=cos2x－－2sinxcosx．

(1)求f(x)的最小正周期；

(2)求证：当x∈时，f(x)≥－．

14.已知函数f(x)=sinωx－cosωx(ω>0)的最小正周期为π．

(1)求函数y=f(x)图象的对称轴方程；

(2)讨论函数f(x)在0，上的单调性．

15.已知函数f(x)=sin2x＋sinxcosx．

(1)求f(x)的最小正周期；

(2)若f(x)在区间－，m上的最大值为，求m的最小值．

16.设函数f(x)=sinω(x－)＋sinω(x－)，其中0<ω<3．已知f()=0．

(1)求ω；

(2)将函数y=f(x)的图象上各点的横坐标伸长为原来的2倍(纵坐标不变)，再将得到的图象向左平移个单位，得到函数y=g(x)的图象，求g(x)在[－，]上的最小值．

答案解析

1.答案为:B；

解析：由题图知A=2，=－=，∴T=π，∴ω=2，∴f(x)=2cos(2x＋φ)，

将代入得cos=1，∵－π<φ<0，∴－<＋φ<，

∴＋φ=0，∴φ=－，∴f(x)=2cos=2sin，

故将函数y=f(x)的图象向左平移个单位长度可得到g(x)的图象．

2.答案为:B　

解析：函数f(x)=tan的图象向右平移个单位长度后所得图象对应的函数

解析式为f(x)=tan=tan，

∵平移后的图象与函数f(x)的图象重合，

∴－＋=＋kπ，k∈Z，解得ω=－6k，k∈Z.又0<ω<10，∴ω=6.故选B.

3.答案为:A；

解析：将函数y=sin的图象向右平移个单位长度后的解析式为：

y=sin=sin 2x则函数y=sin 2x的一个单调递增区间为，

一个单调递减区间为.由此可判断选项A正确．

4.答案为:A；

解析：令x=0，得y=sin=－，排除B、D.由f=0，f=0，排除C，故选A.

5.答案为：C.

解析：将函数f(x)=2sin的图象向左平移个单位，

可得函数y=2sin=2sin的图象；

再把所有点的横坐标缩短到原来的，纵坐标不变，得到函数y=g(x)=2sin的图象，

故g(x)的周期为=，排除A，B.

令x=－，求得g(x)=0，可得g(x)的一个对称中心为，故C满足条件．

在区间上，4x＋∈，函数g(x)没有单调性，故排除D.

6.答案为：B.

解析：将函数y=2sin 2x的图象向左平移个单位长度，

得到函数y=2sin 2=2sin的图象．由2x＋=kπ＋(k∈Z)，

得x=＋(k∈Z)，即平移后图象的对称轴为x=＋(k∈Z)．

7.答案为:A；

解析：设函数f(x)的最小正周期为T.由题图及|MN|=，得=，则T=6，ω=.

又由f(0)=1，φ∈得sin φ=，φ=.

所以f(x)=2sinx＋.则g(x)=2sin=2cos x.故选A.

8.B   

一         、填空题

9.答案为：6 000;

解析：作出函数简图如图：三角函数模型为：y=Asin(ωx＋φ)＋B，

由题意知：A=2000，B=7 000，T=2×(9－3)=12，∴ω==.

将(3，9 000)看成函数图象的第二个特殊点，则有×3＋φ=，∴φ=0，

故f(x)=2 000sinx＋7 000(1≤x≤12，x∈N*)．

∴f(7)=2 000×sin＋7 000=6 000.故7月份的出厂价格为6 000元．

10.答案为：－0.8；

解析：由角φ的终边经过点P(－4，3)，可得cos φ=－.

根据函数f(x)=sin(ωx＋φ)(ω＞0)的图象的相邻两条对称轴之间的距离等于，

可得周期为=2×，解得ω=2，∴f(x)=sin(2x＋φ)，

∴f=sin=cos φ=－.

11.答案为：右，；

12.答案为：sin；

解析：依题意得 =2，ω>0，所以ω=，所以f(x)=sin.

因为该函数图象过点，所以sin(π＋φ)=－，即sin φ=.

因为－≤φ≤，所以φ=，所以f(x)=sin.

二         、解答题

13.解：

(1)f(x)=cos2x＋sin2x－sin2x=sin2x＋cos2x=sin，

所以f(x)的最小正周期T==π．

(2)证明：因为－≤x≤，所以－≤2x＋≤，

所以sin≥sin=－，

所以当x∈时，f(x)≥－．

14.解：

(1)∵f(x)=sinωx－cosωx=sinωx－，且T=π，∴ω=2．

于是f(x)=sin2x－．

令2x－=kπ＋(k∈Z)，得x=＋(k∈Z)，

故函数f(x)的对称轴方程为x=＋(k∈Z)．

(2)令2kπ－≤2x－≤2kπ＋(k∈Z)，

得函数f(x)的单调增区间为kπ－，kπ＋(k∈Z)．

注意到x∈0，，令k=0，得函数f(x)在0，上的单调增区间为0，；

其单调减区间为(，)．

15.解：

(1)f(x)=－cos2x＋sin2x=sin2x－＋．

所以f(x)的最小正周期为T==π．

(2)由(1)知f(x)=sin2x－＋．

由题意知－≤x≤m．所以－≤2x－≤2m－．

要使f(x)在－，m上的最大值为，即需sin2x－在－，m上的最大值为1．

所以2m－≥，即m≥．所以m的最小值为．

16.解:

(1)因为f(x)=sinωx－＋sinωx－，

所以f(x)=sinωx－cosωx－cosωx

=sinωx－cosωx=sinωx－cosωx

=sinωx－．

由题设知f=0，所以－=kπ，k∈Z．

故ω=6k＋2，k∈Z，又0<ω<3，所以ω=2．

(2)由(1)得f(x)=sin2x－，

所以g(x)=sinx＋－=sinx－．

因为x∈－，，所以x－∈－，，

当x－=－，即x=－时，g(x)取得最小值－．