高考数学一轮复习考点测试刷题本22 两角和与差的正弦（含答案解析）

这是一份高考数学一轮复习考点测试刷题本22 两角和与差的正弦（含答案解析），共6页。
2020高考数学(文数)考点测试刷题本22 两角和与差的正弦 一         、选择题1.若2cosθ-=3cos θ，则tan θ=(　　)A.                B.           C．-            D. 2.已知tan α=，tan=，则m=(　　)A．-6或1           B．-1或6              C．6               D．1 3.sin 45°cos 15°＋cos 225°sin 165°=(　　)A．1　　         B.            C.             D．- 4.若sin(α-β)sin β-cos(α-β)cos β=，且α为第二象限角，则tan=(　　)A．7               B.           C．-7              D．- 5.已知tan=，则的值为(　　)A.              B．2           C．2          D．－2 6.已知角α∈，且cos 2α＋cos2α=0，则tan=(　　)A．-3-2          B．-1          C．3-2           D．3＋2 7.设当x=θ时，函数f(x)=sin x-2cos x取得最大值，则cos θ=(　　)A.             B.            C．-           D．- 8.函数的部分图像大致为( 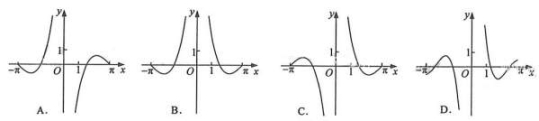     ) 二         、填空题9.已知sin(2α-β)=，sin β=-，且α∈，β∈，则sin α值为_______． 10.已知cos＋sin α=，则sin的值是________． 11.函数f(x)=2cos2x＋sin 2x的最小值是________. 12.若a，b是非零实数，且=tan，则=________． 三         、解答题13.已知α，β为锐角，tanα=，cos(α＋β)=－．(1)求cos2α的值；(2)求tan(α－β)的值．            14.已知角α的顶点与原点O重合，始边与x轴的非负半轴重合，它的终边过点P.(1)求sin(α＋π)的值；(2)若角β满足sin(α＋β)=，求cos β的值．              15.已知A、B、C是△ABC的三个内角且lgsinA－lgsinB－lgcosC=lg2．试判断此三角形的形状特征．               16.已知f(x)=sin2x－2sinsin．(1)若tanα=2，求f(α)的值；(2)若x∈，求f(x)的取值范围．                   
答案解析1.答案为：D； 2.答案为：A； 3.答案为：B； 4.答案为：B； 5.答案为：B. 6.答案为：A；解析：由题意结合二倍角公式可得2cos2α-1＋cos2α=0，∴cos2α=.∵α∈，∴cos α=，∴sin α==，∴tan α==，tan===-3-2，故选A.7.答案为：C；解析：利用辅助角公式可得f(x)=sin x-2cos x=sin(x-φ)，其中cos φ=，sin φ=.当函数f(x)=sin x-2cos x取得最大值时，θ-φ=2kπ＋(k∈Z)，∴θ=2kπ＋＋φ(k∈Z)，则cos θ=cos=-sin φ=-(k∈Z)，故选C.8.【答案】C  9.答案为：；解析：∵<α<π，∴π<2α<2π.∵-<β<0，∴0<-β<，π<2α-β<.∵sin(2α-β)=>0，∴2π<2α-β<，cos(2α-β)=.∵-<β<0且sin β=-，∴cos β=.∴cos 2α=cos[(2α-β)＋β]=cos(2α-β)cos β-sin(2α-β)·sin β=×-×=.∵cos 2α=1-2sin2α，∴sin2α=.∵α∈，∴sin α=. 10.答案为：－0.8； 11.答案：1－； 12.答案为：； 13.解：(1)因为tanα=，tanα=，所以sinα=cosα．因为sin2α＋cos2α=1，所以cos2α=，所以cos2α=2cos2α－1=－．(2)因为α，β为锐角，所以α＋β∈(0，π)．又因为cos(α＋β)=－，所以sin(α＋β)==，因此tan(α＋β)=－2．因为tanα=，所以tan2α==－．因此tan(α－β)=tan[2α－(α＋β)]==－． 14.解：(1)由角α的终边过点P得sin α=－，所以sin(α＋π)=－sin α=.(2)由角α的终边过点P得cos α=－，由sin(α＋β)=得cos(α＋β)=±.由β=(α＋β)－α得cos β=cos(α＋β)cos α＋sin(α＋β)sin α，所以cos β=－或cos β=. 15.分析：从角与角的关系探究三角函数间的关系；反之，利用三角函数间的关系去判断角的大小及关系，这是常用的基本方法．可以先化去对数符号，将对数式转化为有理式，然后再考察A、B、C的关系及大小，据此判明形状特征．解：由于lgsinA－lgsinB－lgcosC=lg2，可得lgsinA=lg2+lgsinB+lgcosC，即lgsinA=lg2sinBcosC，sinA=2sinBcosC．根据内角和定理，A+B+C=π，∴A=π－（B+C）．∴sin（B+C）=2sinBcosC，即sinBcosC+cosBsinC=2sinBcosC．移项化为sinCcosB－sinBcosC=0，即sin（B－C）=0．∴在△ABC中，C=B．∴△ABC为等腰三角形．16.解：(1)f(x)=(sin2x＋sinxcosx)＋2sin·cos=＋sin2x＋sin=＋(sin2x－cos2x)＋cos2x=(sin2x＋cos2x)＋．由tanα=2，得sin2α===，cos2α===－，所以，f(α)=(sin2α＋cos2α)＋=．(2)由(1)得，f(x)=(sin2x＋cos2x)＋=sin＋．由x∈，得≤2x＋≤．所以－≤sin≤1,0≤f(x)≤，所以f(x)的取值范围是．