高考数学一轮复习考点测试刷题本27 平面向量的数量积及应用（含答案解析）

这是一份高考数学一轮复习考点测试刷题本27 平面向量的数量积及应用（含答案解析），共8页。
2020高考数学(文数)考点测试刷题本27 平面向量的数量积及应用 一         、选择题1.已知向量a=(－2，－1)，b=(m,1)，m∈R，若a⊥b，则m的值为(　　)A．－           B．          C．2          D．－2  2.已知向量=(k,12)，=(4,5)，=(－k,10)，且A，B，C三点共线，则k的值是(　　)A．－          B.           C.           D.  3.若两个非零向量a，b满足|a＋b|=|a－b|=2|b|，则向量a＋b与a的夹角为(　　)A．         B．         C．         D．  4.在平行四边形ABCD中，已知AB=5，AD=3，|＋|=4，则·=(　　)A．5         B．9           C．12          D．16  5.若O为△ABC所在平面内任一点，且满足(－)·(＋－2)=0，则△ABC的形状为(　　)A．等腰三角形      B．直角三角形       C．等边三角形      D．等腰直角三角形  6.已知向量a，b满足|a|=1，a·b=－1，则a·(2a－b)=(　　)A．4           B．3           C．2          D．0  7.已知△ABC是边长为2的等边三角形，P为平面ABC内一点，则·(＋)的最小值是(　　)A．－2         B．－          C．－           D．－1  8.已知a，b，e是平面向量，e是单位向量．若非零向量a与e的夹角为，向量b满足b2－4e·b＋3=0，则|a－b|的最小值是(　　)A．－1           B．＋1         C．2         D．2－   二         、填空题9.已知向量a=(1,2)，b=(3,4)，则a＋b=________.  10.在梯形ABCD中，AB∥CD，AB=2CD，M，N分别为CD，BC的中点，若=λ＋μ，则λ＋μ等于________．  11.已知在直角三角形ABC中，∠ACB=90°，AC=BC=2，点P是斜边AB上的中点，则·＋·=________．  12.已知a，b是单位向量，a·b=0，若向量c满足|c－a－b|=1，则|c|的最大值是________．   三         、解答题13.已知A，B，C是△ABC的内角，a，b，c分别是其对边长，向量m=(，cosA＋1)，n=(sinA，－1)，m⊥n．(1)求角A的大小；(2)若a=2，cosB=，求b的值．                         14.在平面直角坐标系xOy中，已知向量m=，n=(sinx，cosx)，x∈．(1)若m⊥n，求tanx的值；(2)若m与n的夹角为，求x的值．                 15.已知向量a=(cosx，sinx)，b=(3，－)，x∈[0，π]．(1)若a∥b，求x的值；(2)记f(x)=a·b，求f(x)的最大值和最小值以及对应的x的值．                           16.已知m=(2，1)，n=cos2，sin(B＋C)，其中A，B，C是△ABC的内角．(1)当A=时，求|n|的值；(2)若BC=1，||=，当m·n取最大值时，求A的大小及AC边的长．              
答案解析1.答案为：A；  2.答案为：A；解析：=－=(4－k，－7)，=－=(－2k，－2)．∵A，B，C三点共线，∴，共线，∴－2×(4－k)=－7×(－2k)，解得k=－.  3.答案为：D；解析：由|a＋b|=|a－b|两边平方得a·b=0．再由|a＋b|=2|b|两边平方得|a|=|b|．从而有cos〈a＋b，a〉====，所以〈a＋b，a〉=，故选D．  4.答案为：B；解析：如图，因为＋=，所以|＋|=||=4．又AB=5，AD=3，所以AD⊥BD．所以·=||||cos〈，〉=5×3×=9．故选B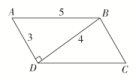．  5.答案为：A；解析：因为(－)·(＋－2)=0，即·(＋)=0，(－)·(＋)=0，即||=||，所以△ABC是等腰三角形，故选A．  6.答案为：B；解析：因为a·(2a－b)=2a2－a·b=2|a|2－(－1)=2＋1=3．故选B．  7.答案为：B；解析：以AB所在直线为x轴，AB的中点为原点建立平面直角坐标系，如图，则A(－1,0)，B(1,0)，C(0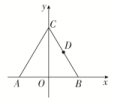，)，设P(x，y)，取BC的中点D，则D，．·(＋)=2·=2(－1－x，－y)·－x，－y=2(x＋1)·x－＋y·y－=2x＋2＋y－2－．因此，当x=－，y=时，·(＋)取得最小值，为2×－=－．故选B．  8.答案为：A；解析：设=a，=b，=e，以O为原点，的方向为x轴正方向建立平面直角坐标系，则E(1,0)．不妨设A点在第一象限，∵a与e的夹角为，∴点A在从原点出发，倾斜角为，且在第一象限内的射线上．设B(x，y)，由b2－4e·b＋3=0，得x2＋y2－4x＋3=0，即(x－2)2＋y2=1，即点B在圆(x－2)2＋y2=1上运动．而=a－b，∴|a－b|的最小值即为点B到射线OA的距离的最小值，即为圆心(2,0)到射线y=x(x≥0)的距离减去圆的半径，所以|a－b|min=－1．故选A．   一         、填空题9.答案为：(4,6)；解析：a＋b=(1,2)＋(3,4)=(4,6)．  10.答案为：0.8；解析：因为=＋=＋=＋(＋)=2＋＋=2－－，所以=－，∴λ=－，μ=.所以λ＋μ=.  11.答案为：4；解析：由题意可建立如图所示的坐标系．可得A(2,0)，B(0,2)，P(1，1)，C(0,0)，则·＋·=(1,1)·(0,2)＋(1,1)·(2,0)=2＋2=4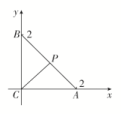．  12.答案为：＋1；解析：因为a，b是单位向量，a·b=0，设a=(1,0)，b=(0,1)，c=(x，y)，则c－a－b=(x－1，y－1)，所以|c－a－b|==1，即(x－1)2＋(y－1)2=1，所以向量c的模|c|=表示圆(x－1)2＋(y－1)2=1上的动点与原点的距离，最大值为＋1=＋1．   二         、解答题13.解：(1)∵m⊥n，∴m·n=sinA＋(cosA＋1)×(－1)=0，∴sinA－cosA=1，∴sinA－=．∴0<A<π，∴－<A－<，∴A－=，∴A=．(2)在△ABC中，A=，a=2，cosB=，∴sinB===．由正弦定理知=，∴b===．  14.解：(1)∵m⊥n，∴m·n=0，故sinx－cosx=0，∴tanx=1．(2)∵m与n的夹角为，∴cos〈m，n〉===，故sin=．又x∈，∴x－∈，x－=，即x=，故x的值为．  15.解：(1)因为a=(cosx，sinx)，b=(3，－)，a∥b，所以－cosx=3sinx．若cosx=0，则sinx=0，与sin2x＋cos2x=1矛盾，故cosx≠0，于是tanx=－．又x∈[0，π]，所以x=．(2)f(x)=a·b=(cosx，sinx)·(3，－)=3cosx－sinx=2cosx＋．因为x∈[0，π]，所以x＋∈，，从而－1≤cosx＋≤．于是，当x＋=，即x=0时，f(x)取到最大值3；当x＋=π，即x=时，f(x)取到最小值－2．  16.解：(1)∵当A=时，n==，∴|n|= =.(2)∵m·n=2cos2＋sin(B＋C)=(1＋cos A)＋sin A=2sin＋.∵0＜A＜π，∴＜A＋＜.∴当A＋=，即A=时，sin=1，此时m·n取得最大值2＋.由余弦定理得BC2=AB2＋AC2－2AB·ACcos A，即12=()2＋AC2－2AC×，化简得AC2－3AC＋2=0，解得AC=1或2.