高考数学一轮复习考点测试刷题本40 空间几何体的表面积和体积（含答案解析）

这是一份高考数学一轮复习考点测试刷题本40 空间几何体的表面积和体积（含答案解析），共10页。
2020高考数学(文数)考点测试刷题本40 空间几何体的表面积和体积 一         、选择题1.如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则该几何体的表面积为(　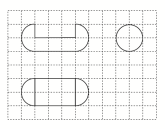　)A．5π＋18       B．6π＋18      C．8π＋6        D．10π＋6  2.如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，已知该几何体的各个面中有n个面是矩形，体积为V，则(　　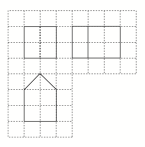)A．n=4，V=10         B．n=5，V=12      C．n=4，V=12         D．n=5，V=10  3.某几何体的三视图如图所示(单位：cm)，则该几何体的体积(单位：cm3)是(　　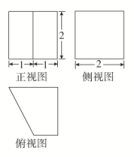)A．2          B．4             C．6             D．8        4.已知一个几何体的三视图如图所示，则其体积为(　　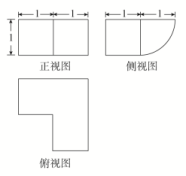)A．10＋π           B．2＋         C．2＋           D．2＋  5.某几何体的三视图如图所示，图中三个正方形的边长均为2，则该几何体的表面积为(　　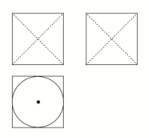)A．24＋(－1)π            B．24＋(2－2)πC．24＋(－1)π            D．24＋(2－2)π  6.若某几何体的三视图(单位：cm)如图所示，则该几何体的体积等于(　　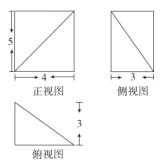)A．10 cm3          B．20 cm3         C．30 cm3           D．40 cm3  7.设A，B，C，D是同一个半径为4的球的球面上四点，△ABC为等边三角形且其面积为9，则三棱锥D－ABC体积的最大值为(　　)A．12           B．18             C．24           D．54      8.我国古代的《九章算术》中将上、下两面为平行矩形的六面体称为“刍童”．如图所示为一个“刍童”的三视图，其中正视图及侧视图均为等腰梯形，两底的长分别为2和4，高为2，则该“刍童”的表面积为(　　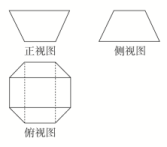)A．12          B．40       C．16＋12        D．16＋12 二         、填空题9.已知圆锥的顶点为S，母线SA，SB所成角的余弦值为，SA与圆锥底面所成角为45°，若△SAB的面积为5，则该圆锥的侧面积为________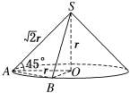．  10.我国古代数学名著《数书九章》中有“天池盆测雨”题：在下雨时，用一个圆台形的天池盆接雨水，天池盆盆口直径为二尺八寸，盆底直径为一尺二寸，盆深一尺八寸，若盆中积水深九寸，则平地降雨量是________寸．(注：①平地降雨量等于盆中积水体积除以盆口面积；②一尺等于十寸)  11.如图，在平面四边形ABCD中，已知AB⊥AD，AB=AD=1，BC=CD=5，以直线AB为轴，将四边形ABCD旋转一周，则所得旋转体的体积为________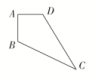．  12.已知正方体ABCD－A1B1C1D1的棱长为1，除面ABCD外，该正方体其余各面的中心分别为点E，F，G，H，M(如图)，则四棱锥M－EFGH的体积为________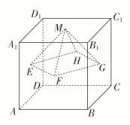．   三         、解答题13.如图，一个圆锥的底面半径为2，高为4，在其中有一个高为x的内接圆柱．(1)求圆柱的侧面积；(2)当x为何值时，圆柱的侧面积最大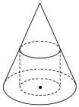？            14.如图，已知某几何体的三视图如下(单位：cm)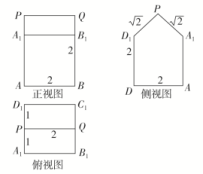．(1)画出这个几何体的直观图(不要求写画法)；(2)求这个几何体的表面积及体积．                  15.现需要设计一个仓库，它由上下两部分组成，上部的形状是正四棱锥P－A1B1C1D1，下部的形状是正四棱柱ABCD－A1B1C1D1(如图所示)，并要求正四棱柱的高O1O是正四棱锥的高PO1的4倍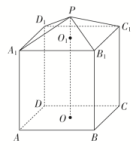．(1)若AB=6 m，PO1=2 m，则仓库的容积是多少？(2)若正四棱锥的侧棱长为6 m，则当PO1为多少时，仓库的容积最大？             16.如图，在平行四边形ABCM中，AB=AC=3，∠ACM=90°，以AC为折痕将△ACM折起，使点M到达点D的位置，且AB⊥DA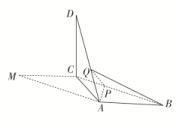．(1)证明：平面ACD⊥平面ABC；(2)Q为线段AD上一点，P为线段BC上一点，且BP=DQ=DA，求三棱锥Q－ABP的体积．               答案解析1.答案为：C；解析：该几何体的表面积是由球的表面积、球的大圆面积、半个圆柱的侧面积以及圆柱的纵切面面积组成．从而该几何体的表面积为4π×12＋π×12＋×2π×3＋3×2=8π＋6．故选C．  2.答案为：D；解析：由三视图可知，该几何体为直五棱柱，其直观图如图所示，故n=5，体积V=2×22＋×2×1=10．故选D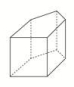．  3.答案为：C  4.答案为：D；解析：根据几何体的三视图还原其直观图如图所示，显然可以看到该几何体是一个底面长为2，宽为1，高为1的正棱柱与一个底面半径为1，高为1的圆柱组合而成，其体积为V=2×1×1＋×π×12×1=2＋，故选D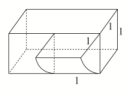．  5.答案为：B；解析：如图，由三视图可知，该几何体是棱长为2的正方体挖出两个圆锥体所得．由图中知圆锥的半径为1，母线为，该几何体的表面积为S=6×22－2π×12＋2××2π×1×=24＋(2－2)π，故选B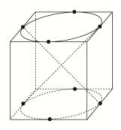．  6.答案为：B解析：由三视图可知，该几何体是一个直三棱柱ABC－A1B1C1截去一个三棱锥B1－ABC，则该几何体的体积为V=×3×4×5－××3×4×5=20(cm3)．故选B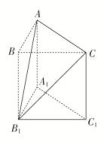．  7.答案为：B；解析：如图所示，点M为三角形ABC的重心，E为AC的中点，当DM⊥平面ABC时，三棱锥D－ABC体积最大，此时，OD=OB=R=4．∵S△ABC=AB2=9，∴AB=6，∵点M为三角形ABC的重心，∴BM=BE=2，∴在Rt△OMB中，有OM==2．∴DM=OD＋OM=4＋2=6，∴(V三棱锥D－ABC)max=×9×6=18．故选B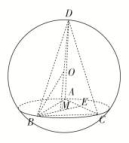．  8.答案为：D；解析：易得侧面梯形的高为=，所以一个侧面梯形的面积为×(2＋4)×=3．故所求为4×3＋2×(2×4)=12＋16．故选D．   一         、填空题9.答案为：40π；解析：如图，∵SA与底面成45°角，∴△SAO为等腰直角三角形．设OA=r，则SO=r，SA=SB=r.在△SAB中，cos∠ASB=，∴sin∠ASB=，∴S△SAB=SA·SB·sin∠ASB=×(r)2×=5，解得r=2，∴SA=r=4，即母线长l=4，∴S圆锥侧=πrl=π×2×4=40π.  10.答案为：3；解析：由题意知，圆台中截面圆的半径为十寸，圆台内水的体积为V=πh(r＋r＋r中r下)=×9×(102＋62＋10×6)=588π(立方寸)，降雨量为==3(寸)．  11.答案为：12π解析：由题意，该旋转体是一圆台内部挖去一个圆锥，如图1所示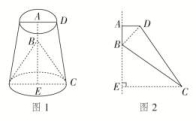：如图2，过点C作CE⊥AB，连接BD．在等腰直角三角形ABD中，BD==．在△BDC中，CD2=BD2＋BC2－2BD·BCcos∠DBC，所以25=2＋25－10cos∠DBC，所以cos∠DBC=，所以sin∠DBC==．因为∠CBE=180°－∠ABD－∠DBC=135°－∠DBC，所以sin∠CBE=sin(135°－∠DBC)=cos∠DBC＋sin∠DBC=．在Rt△BCE中，CE=BCsin∠CBE=4，所以BE==3，AE=4．所以圆台上、下底面圆的面积分别为S上=π，S下=16π，圆台体积V1=(S上＋S下＋)·AE=28π，圆锥体积V2=×16π×3=16π，所以旋转体体积V=V1－V2=12π．  12.答案为：；解析：由题意知四棱锥的底面EFGH为正方形，其边长为，即底面面积为，由正方体的性质知，四棱锥的高为．故四棱锥M－EFGH的体积V=××=．   二         、解答题13.解：(1)如图，设内接圆柱底面半径为r.S圆柱侧=2πr·x.①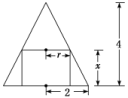∵=，∴r=(4－x)．②②代入①，S圆柱侧=2πx·(4－x)=π(－x2＋4x)(0<x<4)．(2)S圆柱侧=π(－x2＋4x)=π[－(x－2)2＋4]，∴x=2时，S圆柱侧最大=4π.  14.解：(1)这个几何体的直观图如图所示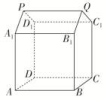．(2)这个几何体可看成是正方体AC1及直三棱柱B1C1Q－A1D1P的组合体．由PA1=PD1=，A1D1=AD=2，可得PA1⊥PD1．故所求几何体的表面积S=5×22＋2×2×＋2××()2=22＋4(cm2)，所求几何体的体积V=23＋×()2×2=10(cm3)．  15.解：(1)由PO1=2知，O1O=4PO1=8．因为A1B1=AB=6，所以正四棱锥P－A1B1C1D1的体积V锥=·A1B·PO1=×62×2=24(m3)．正四棱柱ABCD－A1B1C1D1的体积V柱=AB2·O1O=62×8=288(m3)．所以仓库的容积V=V锥＋V柱=24＋288=312(m3)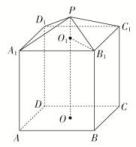．(2)设A1B1=a m，PO1=h m，则0<h<6，O1O=4h．连接O1B1．因为在Rt△PO1B1中，O1B＋PO=PB，所以2＋h2=36，即a2=2(36－h2)．于是仓库的容积V=V柱＋V锥=a2·4h＋a2·h=a2h=(36h－h3)，0<h<6，从而V′=(36－3h2)=26(12－h2)．令V′=0，得h=2或h=－2(舍)．当0<h<2时，V′>0，V是单调增函数；当2<h<6时，V′<0，V是单调减函数．故h=2时，V取得极大值，也是最大值．因此，当PO1=2 m时，仓库的容积最大．  16.解：(1)证明：由已知可得∠BAC=90°，即AB⊥AC．又AB⊥DA，且AC∩DA=A，所以AB⊥平面ACD．又AB⊂平面ABC，所以平面ACD⊥平面ABC．(2)由已知可得，DC=CM=AB=AC=3，DA=3．又BP=DQ=DA，所以BP=2．作QE⊥AC，垂足为E，则QE綊DC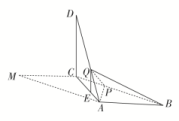．由已知及(1)可得DC⊥平面ABC，所以QE⊥平面ABC，QE=1．因此，三棱锥Q－ABP的体积为V三棱锥Q－ABP=×QE×S△ABP=×1××3×2sin45°=1．