高考数学一轮复习考点测试刷题本41 空间点、直线、平面间的位置关系（含答案解析）

这是一份高考数学一轮复习考点测试刷题本41 空间点、直线、平面间的位置关系（含答案解析），共9页。
2020高考数学(文数)考点测试刷题本41 空间点、直线、平面间的位置关系 一         、选择题1.已知异面直线a，b分别在平面α，β内，且α∩β=c，那么直线c一定(　　)A．与a，b都相交B．只能与a，b中的一条相交C．至少与a，b中的一条相交D．与a，b都平行  2.若空间中n个不同的点两两距离都相等，则正整数n的取值(　　)A．至多等于3    B．至多等于4      C．等于5         D．大于5  3.已知直线a，b分别在两个不同的平面α，β内，则“直线a和直线b相交”是“平面α和平面β相交”的(　　)A．充分不必要条件           B．必要不充分条件C．充要条件                 D．既不充分也不必要条件  4.已知直线l和平面α，无论直线l与平面α具有怎样的位置关系，在平面α内总存在一条直线与直线l(　　)A．相交      B．平行        C．垂直           D．异面  5.如图，已知在正方体ABCD－A1B1C1D1中，AC∩BD=F，DC1∩CD1=E，则直线EF是平面ACD1与(　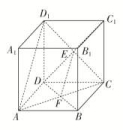　)A．平面BDB1的交线   B．平面BDC1的交线   C．平面ACB1的交线   D．平面ACC1的交线  6.设直线m与平面α相交但不垂直，则下列说法中正确的是(　　)A．在平面α内有且只有一条直线与直线m垂直B．过直线m有且只有一个平面与平面α垂直C．与直线m垂直的直线不可能与平面α平行D．与直线m平行的平面不可能与平面α垂直     7.下列正方体或四面体中，P，Q，R，S分别是所在棱的中点，这四点不共面的一个图是(　　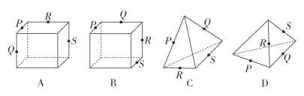) 8.在正方体ABCD－A1B1C1D1中，E为棱CC1的中点，则异面直线AE与CD所成角的正切值为(　　)A．         B．         C．           D． 二         、填空题9.正方体ABCD-A1B1C1D1的棱长为1 cm,过AC作平行于对角线BD1的截面,则截面面积为　　　　cm2. 10.如图所示，在空间四边形A－BCD中，点E，H分别是边AB，AD的中点，点F，G分别是边BC，CD上的点，且==，则下列说法正确的是________．(填写所有正确说法的序号)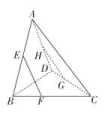①EF与GH平行；②EF与GH异面；③EF与GH的交点M可能在直线AC上，也可能不在直线AC上；④EF与GH的交点M一定在直线AC上．  11.如图，已知圆柱的轴截面ABB1A1是正方形，C是圆柱下底面弧AB的中点，C1是圆柱上底面弧A1B1的中点，那么异面直线AC1与BC所成角的正切值为________.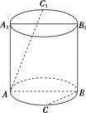12.如图，E是正方体ABCD­A1B1C1D1的棱C1D1上的一点，且BD1∥平面B1CE，则异面直线BD1与CE所成角的余弦值为________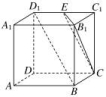．  三         、解答题13.如图，△ABC中，AC=BC=AB，四边形ABED是边长为1的正方形，平面ABED⊥底面ABC，G，F分别是EC，BD的中点．(1)求证：GF∥底面ABC；(2)求几何体ADEBC的体积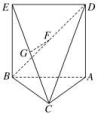．           14.如图，在四棱锥P­ABCD中，PC⊥底面ABCD，四边形ABCD是直角梯形，AB⊥AD，AB∥CD，AB=2AD=2CD=2，E是PB的中点．(1)求证：平面EAC⊥平面PBC；(2)若PC=，求三棱锥C­PAB的高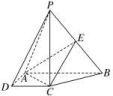．                    15.如图，四棱锥P­ABCD中，AD⊥平面PAB，AP⊥AB.(1)求证：CD⊥AP；(2)若CD⊥PD，求证：CD∥平面PAB. 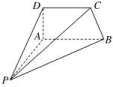             16.如图，四面体ABCD中，△ABC是正三角形，AD=CD．(1)证明：AC⊥BD；(2)已知△ACD是直角三角形，AB=BD，若E为棱BD上与D不重合的点，且AE⊥EC，求四面体ABCE与四面体ACDE的体积比．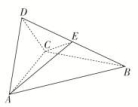          
答案解析1.答案为：C；解析：如果c与a，b都平行，那么由平行线的传递性知a，b平行，与异面矛盾．故选C．  2.答案为：B；解析：首先我们知道正三角形的三个顶点满足两两距离相等，于是可以排除C，D．又注意到正四面体的四个顶点也满足两两距离相等，于是排除A，故选B．  3.答案为：A；解析：因为直线a和直线b相交，所以直线a与直线b有一个公共点，而直线a，b分别在平面α，β内，所以平面α与β必有公共点，从而平面α与β相交；反之，若平面α与β相交，则直线a与直线b可能相交、平行、异面．故选A．  4.答案为：C；解析：当直线l与平面α平行时，在平面α内至少有一条直线与直线l垂直，当直线l⊂平面α时，在平面α内至少有一条直线与直线l垂直，当直线l与平面α相交时，在平面α内至少有一条直线与直线l垂直，所以无论直线l与平面α具有怎样的位置关系，在平面α内总存在一条直线与直线l垂直．  5.答案为：B；解析：连接BC1．因为E∈DC1，F∈BD，所以EF⊂平面BDC1，故平面ACD1∩平面BDC1=EF．故选B．  6.答案为：B；解析：对于A，在平面α内可能有无数条直线与直线m垂直，这些直线是互相平行的，A错误；对于B，因为直线m与平面α相交但不垂直，所以过直线m必有并且也只有一个平面与平面α垂直，B正确；对于C，类似于A，在平面α外可能有无数条直线垂直于直线m并且平行于平面α，C错误；对于D，与直线m平行且与平面α垂直的平面有无数个，D错误．故选B．  7.答案为：D；解析：(利用“经过两条平行直线，有且只有一个平面”判断)对选项A，易判断PR∥SQ，故点P，Q，R，S共面；对选项B，易判断QR∥SP，故点P，Q，R，S共面；对选项C，易判断PQ∥SR，故点P，Q，R，S共面；而选项D中的RS，PQ为异面直线，故选D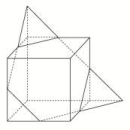．  8.答案为：C；解析：在正方体ABCD－A1B1C1D1中，CD∥AB，所以异面直线AE与CD所成的角为∠EAB，设正方体的棱长为2a，则由E为棱CC1的中点，可得CE=a，所以BE=a，则tan∠EAB===．故选C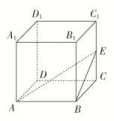．   一         、填空题9.答案　解析　如图所示,截面ACE∥BD1,平面BDD1∩平面ACE=EF,其中F为AC与BD的交点,∴E为DD1的中点,计算可得AE=CE= cm,AC= cm,则EF⊥AC,EF= cm,∴S△ACE=××=(cm2).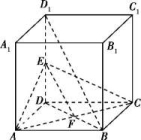10.答案为：④；解析：连接EH，FG(图略)，依题意，可得EH∥BD，FG∥BD，故EH∥FG，所以E，F，G，H共面．因为EH=BD，FG=BD，故EH≠FG，所以四边形EFGH是梯形，EF与GH必相交，设交点为M．因为点M在EF上，故点M在平面ACB上．同理，点M在平面ACD上，所以点M是平面ACB与平面ACD的交点，又AC是这两个平面的交线，所以点M一定在直线AC上．  11.答案为：12.答案为：；解析：不妨设正方体ABCD­A1B1C1D1的棱长为2，连接BC1，设B1C∩BC1=O，连接EO，如图所示，在△BC1D1中，当点E为C1D1的中点时，BD1∥OE，则BD1∥平面B1CE，据此可得∠OEC为直线BD1与CE所成的角．在△OEC中，边长EC=，OC=，OE=，由余弦定理可得cos∠OEC==.即异面直线BD1与CE所成角的余弦值为.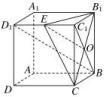   二         、解答题13.解：(1)证明：如图，取BC的中点M，AB的中点N，连接GM，FN，MN.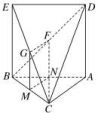∵G，F分别是EC，BD的中点，∴GM∥BE，且GM=BE，NF∥DA，且NF=DA.又四边形ABED为正方形，∴BE∥AD，BE=AD，∴GM∥NF且GM=NF.∴四边形MNFG为平行四边形．∴GF∥MN，又MN⊂平面ABC，GF⊄平面ABC，∴GF∥平面ABC.(2)连接CN，∵AC=BC，∴CN⊥AB，又平面ABED⊥平面ABC，CN⊂平面ABC，∴CN⊥平面ABED.易知△ABC是等腰直角三角形，∴CN=AB=，∵C­ABED是四棱锥，∴VC­ABED=S四边形ABED·CN=×1×=.  14.解：(1)证明：因为PC⊥平面ABCD，AC⊂平面ABCD，所以AC⊥PC.因为AB=2，AD=CD=1，所以AC=BC=，所以AC2＋BC2=AB2，故AC⊥BC.又BC∩PC=C，所以AC⊥平面PBC.因为AC⊂平面EAC，所以平面EAC⊥平面PBC.(2)由PC=，PC⊥CB，得S△PBC=×()2=1.由(1)知，AC为三棱锥A­PBC的高．易知Rt△PCA≌Rt△PCB≌Rt△ACB，则PA=AB=PB=2，于是S△PAB=×22sin 60°=.设三棱锥C­PAB的高为h，则S△PAB·h=S△PBC·AC，×h=×1×，解得h=，故三棱锥C­PAB的高等于. 15.证明：(1)因为AD⊥平面PAB，AP⊂平面PAB，所以AD⊥AP.又AP⊥AB，AB∩AD=A，AB⊂平面ABCD，AD⊂平面ABCD，所以AP⊥平面ABCD.因为CD⊂平面ABCD，所以CD⊥AP.(2)由(1)知CD⊥AP，因为CD⊥PD，PD∩AP=P，PD⊂平面PAD，AP⊂平面PAD，所以CD⊥平面PAD.①因为AD⊥平面PAB，AB⊂平面PAB，所以AB⊥AD.又AP⊥AB，AP∩AD=A，AP⊂平面PAD，AD⊂平面PAD，所以AB⊥平面PAD.②由①②得CD∥AB，因为CD⊄平面PAB，AB⊂平面PAB，所以CD∥平面PAB.  16.解：(1)证明：如图，取AC的中点O，连接DO，BO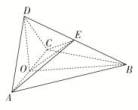．因为AD=CD，所以AC⊥DO．又由于△ABC是正三角形，所以AC⊥BO．从而AC⊥平面DOB，故AC⊥BD．(2)连接EO．由(1)及题设知∠ADC=90°，所以DO=AO．在Rt△AOB中，BO2＋AO2=AB2．又AB=BD，所以BO2＋DO2=BO2＋AO2=AB2=BD2，故∠DOB=90°．由题设知△AEC为直角三角形，所以EO=AC．又△ABC是正三角形，且AB=BD，所以EO=BD．故E为BD的中点，从而E到平面ABC的距离为D到平面ABC的距离的，四面体ABCE的体积为四面体ABCD的体积的，即四面体ABCE与四面体ACDE的体积之比为1∶1．