高考数学一轮复习考点测试刷题本43 直线、平面垂直的判定及其性质（含答案解析）

这是一份高考数学一轮复习考点测试刷题本43 直线、平面垂直的判定及其性质（含答案解析），共9页。
2020高考数学(文数)考点测试刷题本43 直线、平面垂直的判定及其性质 一         、选择题1.若l，m是两条不同的直线，m垂直于平面α，则“l⊥m”是“l∥α”的(　　)A．充分而不必要条件          B．必要而不充分条件C．充分必要条件              D．既不充分也不必要条件  2.已知互不重合的直线a，b，互不重合的平面α，β，γ，给出下列四个命题，错误的命题是(　　)A．若a∥α，a∥β，α∩β=b，则a∥bB．若α⊥β，a⊥α，b⊥β，则a⊥bC．若α⊥β，α⊥γ，β∩γ=a，则a⊥αD．若α∥β，a∥α，则a∥β  3.已知a，b表示两条不同的直线，α，β表示两个不同的平面，下列说法错误的是(　　)A．若a⊥α，b⊥β，α∥β，则a∥bB．若a⊥α，b⊥β，a⊥b，则α⊥βC．若a⊥α，a⊥b，α∥β，则b∥βD．若α∩β=a，a∥b，则b∥α或b∥β  4.如图甲所示，在正方形ABCD中，E，F分别是BC，CD的中点，G是EF的中点，现在沿AE，AF及EF把这个正方形折成一个四面体，使B，C，D三点重合，重合后的点记为H，如图乙所示，那么，在四面体A－EFH中必有(　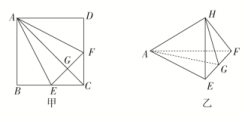　)  A．AH⊥平面EFH      B．AG⊥平面EFH     C．HF⊥平面AEF      D．HG⊥平面AEF  5.如果PA，PB，PC两两垂直，那么点P在平面ABC内的投影一定是△ABC的(　　)A．重心         B．内心            C．外心         D．垂心  6.如图，四棱锥P－ABCD中，△PAB与△PBC是正三角形，平面PAB⊥平面PBC，AC⊥BD，则下列结论不一定成立的是(　　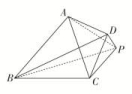)A．PB⊥AC       B．PD⊥平面ABCDC．AC⊥DP       D．平面PBD⊥平面ABCD7.如图所示，在立体图形D－ABC中，若AB=CB，AD=CD，E是AC的中点，则下列结论正确的是(　　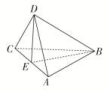)A．平面ABC⊥平面ABDB．平面ABD⊥平面BDCC．平面ABC⊥平面BDE，且平面ADC⊥平面BDED．平面ABC⊥平面ADC，且平面ADC⊥平面BDE  8.如图，已知四边形ABCD是边长为1的正方形，MD⊥平面ABCD，NB⊥平面ABCD，且MD=NB=1，E为MC的中点，则下列结论不正确的是(　　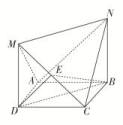)A．平面BCE⊥平面ABN           B．MC⊥ANC．平面CMN⊥平面AMN           D．平面BDE∥平面AMN 二         、填空题9.已知四棱锥P－ABCD的底面ABCD是矩形，PA⊥底面ABCD，点E，F分别是棱PC，PD的中点，则：①棱AB与PD所在的直线垂直；②平面PBC与平面ABCD垂直；③△PCD的面积大于△PAB的面积；④直线AE与直线BF是异面直线．以上结论正确的是________．(写出所有正确结论的序号)  10.如图，直三棱柱ABC­A1B1C1中，侧棱长为2，AC=BC=1，∠ACB=90°，D是A1B1的中点，F是BB1上的动点，AB1，DF交于点E.要使AB1⊥平面C1DF，则线段B1F的长为________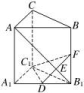．  11.已知α，β为两个不同的平面，m，n为两条不同的直线，则下列命题中正确的是________(填上所有正确命题的序号)．①若α∥β，m⊂α，则m∥β；②若m∥α，n⊂α，则m∥n；③若α⊥β，α∩β=n，m⊥n，则m⊥β；④若n⊥α，n⊥β，m⊥α，则m⊥β.    12.如图所示，在长方形ABCD中，AB=2，BC=1，E为CD的中点，F为线段EC上(端点除外)一动点．现将△AFD沿AF折起，使平面ABD⊥平面ABCF.在平面ABD内过点D作DK⊥AB，K为垂足．设AK=t，则t的取值范围是________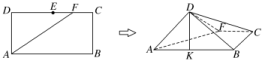． 三         、解答题13.如图，在四棱锥P­ABCD中，PC⊥底面ABCD，四边形ABCD是直角梯形，AB⊥AD，AB∥CD，AB=2AD=2CD=2，E是PB的中点．(1)求证：平面EAC⊥平面PBC；(2)若PC=，求三棱锥C­PAB的高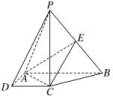．            14.如图，四棱锥P­ABCD中，AD⊥平面PAB，AP⊥AB.(1)求证：CD⊥AP；(2)若CD⊥PD，求证：CD∥平面PAB.               15.如图，在三棱锥P－ABC中，AB=BC=2，PA=PB=PC=AC=4，O为AC的中点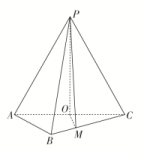．(1)证明：PO⊥平面ABC；(2)若点M在棱BC上，且MC=2MB，求点C到平面POM的距离．               16.如图，在四棱锥P－ABCD中，AD∥BC，AD⊥CD，Q是AD的中点，M是棱PC的中点，PA=PD=2，BC=AD=1，CD=，PB=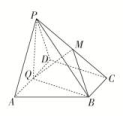．(1)求证：PA∥平面MQB；(2)求证：平面PAD⊥底面ABCD；(3)求三棱锥B－PQM的体积．              
答案解析1.答案为：B；解析：由“m⊥α且l⊥m”推出“l⊂α或l∥α”，但由“m⊥α且l∥α”可推出“l⊥m”，所以“l⊥m”是“l∥α”的必要而不充分条件．故选B．  2.答案为：D；解析：构造一个长方体ABCD－A1B1C1D1．对于D，平面ABCD∥平面A1B1C1D1，A1B1∥平面ABCDA1B1∥平面A1B1C1D1．  3.答案为：C；解析：对于A，若a⊥α，α∥β，则a⊥β，又b⊥β，故a∥b，A正确；对于B，若a⊥α，a⊥b，则b⊂α或b∥α，∴存在直线m⊂α，使得m∥b，又b⊥β，∴m⊥β，∴α⊥β，故B正确；对于C，若a⊥α，a⊥b，则b⊂α或b∥α，又α∥β，∴b⊂β或b∥β，故C错误；对于D，若α∩β=a，a∥b，则b∥α或b∥β，故D正确，故选C．  4.答案为：A；解析：∵AH⊥HE，AH⊥HF，且EH∩HF=H，∴AH⊥平面EFH，A正确；∵过A只有一条直线与平面EFH垂直，∴B不正确；∵AG⊥EF，EF⊥AH，AG∩AH=A，∴EF⊥平面HAG，∵EF⊂平面AEF，∴平面HAG⊥AEF，∴过H作平面AEF的垂线，一定在平面HAG内，∴C不正确；∵HG不垂直于AG，∴HG⊥平面AEF不正确，∴D不正确，故选A．  5.答案为：D；解析：如图，O是点P在平面ABC内的投影，连接OA，OB，OC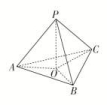，∵PA，PB，PC两两垂直，∴PA⊥平面PBC，又BC⊂平面PBC，∴PA⊥BC，而PO⊥平面ABC，BC⊂平面ABC，∴PO⊥BC，又PA∩PO=P，∴BC⊥平面PAO．又AO⊂平面PAO，∴BC⊥AO．同理可知AC⊥BO，AB⊥CO．∴O为△ABC的垂心．故选D．  6.答案为：B；解析：取BP中点O，连接OA，OC，易得BP⊥OA，BP⊥OC⇒BP⊥面OAC⇒BP⊥AC⇒选项A正确；又AC⊥BD⇒AC⊥面BDP⇒AC⊥PD，平面PBD⊥平面ABCD，所以选项C，D也正确．故选B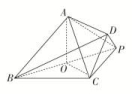．  7.答案为：C；解析：因为AB=CB，且E是AC的中点，所以BE⊥AC，同理有DE⊥AC，而BE∩DE=E，所以AC⊥平面BDE．因为AC在平面ABC内，所以平面ABC⊥平面BDE．又由于AC在平面ADC内，所以平面ADC⊥平面BDE．故选C．  8.答案为：C；解析：分别过A，C作平面ABCD的垂线AP，CQ，使得AP=CQ=1，连接PM，PN，QM，QN，将几何体补成棱长为1的正方体．∴BC⊥平面ABN，又BC⊂平面BCE，∴平面BCE⊥平面ABN，故A正确；连接PB，则PB∥MC，显然，PB⊥AN，∴MC⊥AN，故B正确；取MN的中点F，连接AF，CF，AC．∵△AMN和△CMN都是边长为的等边三角形，∴AF⊥MN，CF⊥MN，∴∠AFC为二面角A－MN－C的平面角，∵AF=CF=，AC=，∵AF2＋CF2≠AC2，即∠AFC≠，∴平面CMN与平面AMN不垂直，故C错误；∵DE∥AN，MN∥BD，DE∩BD=D，DE，BD⊂平面BDE，MN∩AN=N，MN，AN⊂平面AMN，∴平面BDE∥平面AMN，故D正确，故选C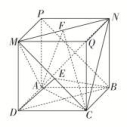． 9.答案为：①③；解析：由条件可得AB⊥平面PAD，∴AB⊥PD，故①正确；∵PA⊥平面ABCD，∴平面PAB，平面PAD都与平面ABCD垂直．故平面PBC不可能与平面ABCD垂直，故②错误；∵S△PCD=CD·PD，S△PAB=AB·PA，由AB=CD，PD>PA，可知③正确；由E，F分别是棱PC，PD的中点可得EF∥CD，又AB∥CD，∴EF∥AB，故AE与BF共面，故④错误．  10.答案为：；解析：设B1F=x，因为AB1⊥平面C1DF，DF⊂平面C1DF，所以AB1⊥DF.由已知可得A1B1=，设Rt△AA1B1斜边AB1上的高为h，则DE=h.又2×=h，所以h=，DE=.在Rt△DB1E中，B1E==.由面积相等得× =x，得x=.  11.答案为：①④；解析：由α∥β，m⊂α，可得m∥β，所以①正确；由m∥α，n⊂α，可得m，n平行或异面，所以②不正确；由α⊥β，α∩β=n，m⊥n，可得m与β相交或m⊂β，所以③不正确；由n⊥α，n⊥β，可得α∥β，又m⊥α，所以m⊥β，所以④正确．综上，正确命题的序号是①④.  12.答案为：；解析：如图①所示，过点K作KM⊥AF于点M，连接DM，易得DM⊥AF，与折前的图形对比，可知折前的图形中D，M，K三点共线且DK⊥AF(如图②所示)，于是△DAK∽△FDA，所以=，即=，所以t=，又DF∈(1,2)，故t∈. 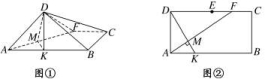13.解：(1)证明：因为PC⊥平面ABCD，AC⊂平面ABCD，所以AC⊥PC.因为AB=2，AD=CD=1，所以AC=BC=，所以AC2＋BC2=AB2，故AC⊥BC.又BC∩PC=C，所以AC⊥平面PBC.因为AC⊂平面EAC，所以平面EAC⊥平面PBC.(2)由PC=，PC⊥CB，得S△PBC=×()2=1.由(1)知，AC为三棱锥A­PBC的高．易知Rt△PCA≌Rt△PCB≌Rt△ACB，则PA=AB=PB=2，于是S△PAB=×22sin 60°=.设三棱锥C­PAB的高为h，则S△PAB·h=S△PBC·AC，×h=×1×，解得h=，故三棱锥C­PAB的高等于. 14.证明：(1)因为AD⊥平面PAB，AP⊂平面PAB，所以AD⊥AP.又AP⊥AB，AB∩AD=A，AB⊂平面ABCD，AD⊂平面ABCD，所以AP⊥平面ABCD.因为CD⊂平面ABCD，所以CD⊥AP.(2)由(1)知CD⊥AP，因为CD⊥PD，PD∩AP=P，PD⊂平面PAD，AP⊂平面PAD，所以CD⊥平面PAD.①因为AD⊥平面PAB，AB⊂平面PAB，所以AB⊥AD.又AP⊥AB，AP∩AD=A，AP⊂平面PAD，AD⊂平面PAD，所以AB⊥平面PAD.②由①②得CD∥AB，因为CD⊄平面PAB，AB⊂平面PAB，所以CD∥平面PAB.  15.解：(1)证明：因为AP=CP=AC=4，O为AC的中点，所以OP⊥AC，且OP=2．连接OB，因为AB=BC=AC，所以△ABC为等腰直角三角形，且OB⊥AC，OB=AC=2．由OP2＋OB2=PB2知OP⊥OB．由OP⊥OB，OP⊥AC，AC∩OB=O，知PO⊥平面ABC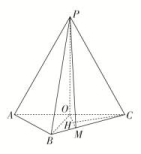．(2)作CH⊥OM，垂足为H．又由(1)可得OP⊥CH，所以CH⊥平面POM．故CH的长为点C到平面POM的距离．由题设可知OC=AC=2，CM=BC=，∠ACB=45°．所以OM=，CH==．所以点C到平面POM的距离为．  16.解：(1)证明：如图，连接AC，交BQ于N，连接MN，QC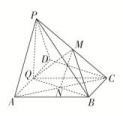，∵BC=AD，AD∥BC，Q是AD的中点，∴AQ∥BC，且AQ=BC，∴四边形ABCQ是平行四边形，∴N是BQ的中点，∵M是棱PC的中点，∴MN∥PA，∵PA⊄平面MQB，MN⊂平面MQB，∴PA∥平面MQB．(2)证明：∵AD∥BC，BC=AD=1，Q是AD的中点，∴BC∥QD，BC=QD，∴四边形BCDQ为平行四边形，∴CD∥BQ，∵AD⊥CD，∴BQ⊥AD．又PA=PD=2，AD=2，Q是AD的中点，故PQ=．又QB=CD=，PB=，∴PB2=PQ2＋QB2，由勾股定理的逆定理可知PQ⊥QB，又PQ∩AD=Q，∴BQ⊥平面PAD，又BQ⊂平面ABCD．∴平面PAD⊥平面ABCD．(3)由(2)可知，PQ=，BQ=，∴PA=PD=2，Q是AD的中点，∴PQ⊥AD，∵平面PAD⊥平面ABCD，且平面PAD∩平面ABCD=AD，∴PQ⊥平面ABCD，又M是棱PC的中点，故VB－PQM=VP－BQC－VM－BQC=VP－BQC－VP－BQC=VP－BQC=×××1××=．