高考数学一轮复习考点测试刷题本50 圆锥曲线综合题（含答案解析）

这是一份高考数学一轮复习考点测试刷题本50 圆锥曲线综合题（含答案解析），共9页。
2020高考数学(文数)考点测试刷题本50 圆锥曲线综合题1.在平面直角坐标系中，直线不过原点，且与椭圆有两个不同的公共点A，B．（Ⅰ）求实数m取值所组成的集合M；（Ⅱ）是否存在定点P使得任意的m∈M，都有直线PA，PB的倾斜角互补．若存在，求出所有定点P的坐标；若不存在，请说明理由．          2.如图，已知抛物线，点A，，抛物线上的点.过点B作直线AP的垂线，垂足为Q.（Ⅰ）求直线AP斜率的取值范围；（Ⅱ）求的最大值.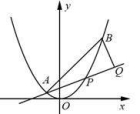          3.已知椭圆C：，离心率为．（I）求椭圆C的标准方程；（Ⅱ）设椭圆C的下顶点为A，直线l过定点，与椭圆交于两个不同的点M、N，且满足|AM|=|AN|．求直线l的方程．               4.已知F1、F2分别为椭圆C：(a>b>0)的左、右焦点, 且离心率为，点椭圆C上.（Ⅰ）求椭圆C的方程；（Ⅱ）是否存在斜率为k的直线与椭圆C交于不同的两点M、N，使直线与的倾斜角互补，且直线是否恒过定点，若存在，求出该定点的坐标；若不存在，说明理由。            5.抛物线y2=x与直线x-2y-3=0的两个交点分别为P、Q，点M在抛物线上从P向Q运动（点M不同于点P、Q），（Ⅰ）求由抛物线y2=x与直线x-2y-3=0所围成的封闭图形面积；（Ⅱ）求使⊿MPQ的面积为最大时M点的坐标.                6.已知M为椭圆C：＋=1上的动点，过点M作x轴的垂线，垂足为D，点P满足=.(1)求动点P的轨迹E的方程；(2)若A，B两点分别为椭圆C的左、右顶点，F为椭圆C的左焦点，直线PB与椭圆C交于点Q，直线QF，PA的斜率分别为kQF，kPA，求的取值范围．                    7.已知椭圆C的中心在原点,焦点在x轴上,长轴长为4,且点在椭圆C上.(1)求椭圆C的方程;(2)设P是椭圆C长轴上的一个动点,过点P作斜率为的直线l交椭圆C于A,B两点,求证:|PA|2+|PB|2为定值.                   8.在平面直角坐标系xOy 中，椭圆G的中心为坐标原点，左焦点为F1（﹣1，0），离心率e=．（1）求椭圆G 的标准方程；（2）已知直线l1：y=kx+m1与椭圆G交于 A，B两点，直线l2：y=kx+m2（m1≠m2）与椭圆G交于C，D两点，且|AB|=|CD|，如图所示．①证明：m1+m2=0；②求四边形ABCD 的面积S 的最大值．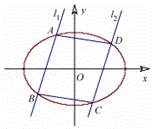 
答案解析1.  2.      3.4.解析：         5.（1） （2）    6.解：(1)设P(x，y)，M(m，n)，依题意知D(m，0)，且y≠0.由=，得(m－x，－y)=(0，－n)，则有⇒又M(m，n)为椭圆C：＋=1上的点，∴＋=1，即x2＋y2=25，故动点P的轨迹E的方程为x2＋y2=25(y≠0)．(2)依题意知A(－5，0)，B(5，0)，F(－4，0)，设Q(x0，y0)，∵线段AB为圆E的直径，∴AP⊥BP，设直线PB的斜率为kPB，则kPA=－，==－kQFkPB=－kQFkQB=－·=－=－===，∵点P不同于A，B两点且直线QF的斜率存在，∴－5＜x0＜5且x0≠－4，又y=在(－5，－4)和(－4，5)上都是减函数，∴∈(－∞，0)∪，故的取值范围是(－∞，0)∪.  7.(1)解 因为2a=4,所以a=2.又因为焦点在x轴上,所以设椭圆方程为=1.将点代入椭圆方程得b2=1,所以椭圆方程为+y2=1.(2)证明 设点P(m,0)(-2≤m≤2),可得直线l的方程是y=,由方程组消去y得2x2-2mx+m2-4=0. (*)设A(x1,y1),B(x2,y2),则x1,x2是方程(*)的两个根.所以x1+x2=m,x1x2=所以|PA|2+|PB|2=(x1-m)2++(x2-m)2+=(x1-m)2+(x1-m)2+(x2-m)2+(x2-m)2=[(x1-m)2+(x2-m)2]=-2m(x1+x2)+2m2]=[(x1+x2)2-2m(x1+x2)-2x1x2+2m2]=[m2-2m2-(m2-4)+2m2]=5.所以|PA|2+|PB|2为定值.  8.