高考数学一轮复习考点测试刷题本53 几何概型（含答案解析）

这是一份高考数学一轮复习考点测试刷题本53 几何概型（含答案解析），共8页。
2020高考数学(文数)考点测试刷题本53 几何概型 一         、选择题1.向等腰直角三角形ABC(其中AC=BC)内任意投一点M，则AM小于AC的概率为(　　)A．          B．1－           C．            D．  2.在长为12 cm的线段AB上任取一点C，现作一矩形，邻边长分别等于线段AC，CB的长，则该矩形的面积大于20 cm2的概率为(　　)A．           B．            C．          D．  3.下图来自古希腊数学家希波克拉底所研究的几何图形．此图由三个半圆构成，三个半圆的直径分别为直角三角形ABC的斜边BC，直角边AB，AC．△ABC的三边所围成的区域记为Ⅰ，黑色部分记为Ⅱ，其余部分记为Ⅲ．在整个图形中随机取一点，此点取自Ⅰ，Ⅱ，Ⅲ的概率分别记为p1，p2，p3，则(　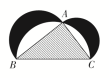　)A．p1=p2           B．p1=p3           C．p2=p3            D．p1=p2＋p3  4.如图，正方形ABCD内的图形来自中国古代的太极图．正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称．在正方形内随机取一点，则此点取自黑色部分的概率是(　　)A．             B．          C．           D．  5.某公司的班车在7：30，8：00，8：30发车，小明在7：50至8：30之间到达发车站乘坐班车，且到达发车站的时刻是随机的，则他等车时间不超过10分钟的概率是(　　)A．           B．           C．            D．     6.从区间[0，1]随机抽取2n个数x1，x2，…，xn，y1，y2，…，yn，构成n个数对(x1，y1)，(x2，y2)，…，(xn，yn)，其中两数的平方和小于1的数对共有m个，则用随机模拟的方法得到的圆周率π的近似值为(　　)A．          B．            C．          D．  7.在区间[0，1]上随机取两个数x，y，记p1为事件“x＋y≤”的概率，p2为事件“xy≤”的概率，则(　　)A．p1<p2<           B．p2<<p1                C．<p2<p1           D．p1<<p2  8.下图是一个边长为4的正方形二维码，为了测算图中黑色部分的面积，在正方形区域内随机投掷400个点，其中落入黑色部分的有225个点，据此可估计黑色部分的面积为(　　)A．8          B．9           C．10          D．12  二         、填空题9.如图所示，在边长为1的正方形中随机撒1000粒豆子，有180粒落到阴影部分，据此估计阴影部分的面积为________． 10.过等腰Rt△ABC的直角顶点C在∠ACB内部随机作一条射线，设射线与AB相交于点D，则AD<AC的概率是________．  11.利用随机模拟方法计算y=x2与y=4围成的面积时，利用计算器产生两组0～1之间的均匀随机数a1=RAND，b1=RAND，然后进行平移与伸缩变换a=a1·4－2，b=b1·4，试验进行100次，前98次中落在所求面积区域内的样本点数为65，已知最后两次试验的随机数a1=0．3，b1=0．8及a1=0．4，b1=0．3，那么本次模拟得出的面积约为________．  12.记函数f(x)=的定义域为D．在区间[－4，5]上随机取一个数x，则x∈D的概率是______．      三         、解答题13.设有一个均匀的陀螺，其圆周的一半上均匀地刻上区间[0，1]上的诸数字，另一半上均匀地刻上区间[1，3]上的诸数字，旋转这陀螺，求它停下时，其圆周上触及桌面的刻度位于[0、5，1、5]上的概率。                14.若张三每天的工作时间在6小时至9小时之间随机均匀分布，求张三连续两天平均工作时间不少于7小时的概率．                          15.某港口有一个泊位，现统计了某月100艘轮船在该泊位停靠的时间(单位：小时)，如果停靠时间不足半小时按半小时计时，超过半小时不足1小时按1小时计时，依此类推，统计结果如下表：(1)设该月100艘轮船在该泊位的平均停靠时间为a小时，求a的值；(2)假定某天只有甲、乙两艘轮船需要在该泊位停靠a小时，且在一昼夜的时间段中随机到达，求这两艘轮船中至少有一艘在停靠该泊位时必须等待的概率．                 16.设f(x)和g(x)都是定义在同一区间上的两个函数，若对任意x∈[1，2]，都有|f(x)＋g(x)|≤8，则称f(x)和g(x)是“友好函数”，设f(x)=ax，g(x)=．(1)若a∈{1，4}，b∈{－1，1，4}，求f(x)和g(x)是“友好函数”的概率；(2)若a∈[1，4]，b∈[1，4]，求f(x)和g(x)是“友好函数”的概率．                    
答案解析1.答案为：D；解析：以A为圆心，AC为半径画弧与AB交于点D．依题意，满足条件的概率P===．故选D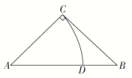．  2.答案为：B；解析：不妨设矩形的长为x cm，则宽为(12－x) cm，由x(12－x)>20，解得2<x<10，所以该矩形的面积大于20 cm2的概率为=．故选B．  3.答案为：A；解析：不妨取AB=AC=2，则BC=2，所以区域Ⅰ的面积为S△ABC=2；区域Ⅲ的面积为π－2；区域Ⅱ的面积为π－(π－2)=2，所以根据几何概型的概率公式，易得p1=p2．故选A．  4.答案为：B；解析：不妨设正方形ABCD的边长为2，则正方形内切圆的半径为1，S正方形=4．由圆中的黑色部分和白色部分关于正方形的中心成中心对称，得S黑=S白=S圆=，所以由几何概型知所求概率P===．故选B．  5.答案为：B；解析：7：30的班车小明显然是坐不到的．当小明在7：50之后8：00之前到达，或者8：20之后8：30之前到达时，他等车的时间将不超过10分钟，故所求概率为=．故选B．  6.答案为：C；解析：如图，数对(xi，yi)(i=1，2，…，n)表示的点落在边长为1的正方形OABC内(包括边界)，两数的平方和小于1的数对表示的点落在半径为1的四分之一圆(阴影部分)内，则由几何概型的概率公式可得=⇒π=．故选C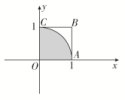．  7.答案为：D；解析：如图，满足条件的x，y构成的点(x，y)在正方形OBCA内，其面积为1．事件“x＋y≤”对应的图形为阴影△ODE，其面积为××=，故p1=<；事件“xy≤”对应的图形为斜线表示部分，其面积显然大于，故p2>，则p1<<p2，故选D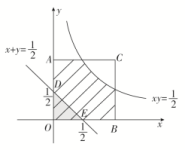．  8.答案为：B；解析：根据面积之比与点数之比相等的关系，得黑色部分的面积S=4×4×=9．故选B． 9.答案为：0．18；解析：由题意知，==0．18．∵S正=1，∴S阴=0．18． 10.答案为：0．75；解析：在AB上取一点E，使AE=AC，连接CE(如图)，则当射线CD落在∠ACE内部时，AD<AC．易知∠ACE=67．5°，∴AD<AC的概率P==0．75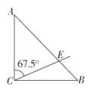． 11.答案为：10．72；解析：由a1=0．3，b1=0．8，得a=－0．8，b=3．2，(－0．8，3．2)落在y=x2与y=4围成的区域内；由a1=0．4，b1=0．3，得a=－0．4，b=1．2，(－0．4，1．2)落在y=x2与y=4围成的区域内，所以本次模拟得出的面积约为16×=10．72． 12.答案为：；解析：由6＋x－x2≥0，解得－2≤x≤3，∴D=[－2，3]．如图，区间[－4，5]的长度为9，定义域D的长度为5，∴P=． 13.14.解：设第一天工作的时间为x小时，第二天工作的时间为y小时，则因为连续两天平均工作时间不少于7小时，所以≥7，即x＋y≥14，表示的区域面积为9，其中满足x＋y≥14的区域面积为9－×2×2=7，∴张三连续两天平均工作时间不少于7小时的概率是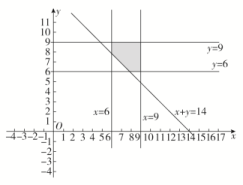． 15.解：(1)a=×(2．5×12＋3×12＋3．5×17＋4×20＋4．5×15＋5×13＋5．5×8＋6×3)=4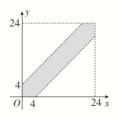．(2)设甲船到达的时间为x，乙船到达的时间为y，则若这两艘轮船在停靠该泊位时至少有一艘船需要等待，则|y－x|<4，符合题意的区域为阴影部分(不包括x，y轴)，所以所求概率P==，则这两艘轮船中至少有一艘在停靠该泊位时必须等待的概率为． 16.解：(1)设事件A表示f(x)和g(x)是“友好函数”，则|f(x)＋g(x)|(x∈[1，2])所有的情况有：x－，x＋，x＋，4x－，4x＋，4x＋，共6种且每种情况被取到的可能性相同．又当a>0，b>0时，ax＋在上递减，在上递增；x－和4x－在(0，＋∞)上递增，∴对x∈[1，2]可使|f(x)＋g(x)|≤8恒成立的有x－，x＋，x＋，4x－，故事件A包含的基本事件有4种，∴P(A)==，故所求概率是．(2)设事件B表示f(x)和g(x)是“友好函数”，∵a是从区间[1，4]中任取的数，b是从区间[1，4]中任取的数，∴点(a，b)所在区域是长为3，宽为3的矩形区域．要使x∈[1，2]时，|f(x)＋g(x)|≤8恒成立，需f(1)＋g(1)=a＋b≤8且f(2)＋g(2)=2a＋≤8，∴事件B表示的点的区域是如图所示的阴影部分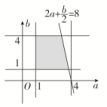．∴P(B)==，故所求概率是．