专题4.1 几何初步-中考数学第一轮总复习课件

这是一份专题4.1 几何初步-中考数学第一轮总复习课件，共23页。PPT课件主要包含了射线线段，角度的计算，平行线，公理定理，∠A-∠C∠AEC，∠A+∠C∠AEC等内容，欢迎下载使用。

【例1】小光准备从A地去往B地，打开导航，显示两地距离为37.5km,但导航提供的三条可选路线长却分别为45km,50km,51km(如图).能解释这一现象的数学知识是( ) A.两点之间,线段最最短； B.两点确定一条直线. C.垂线段最短； D.三角形两边之和大于第三边；
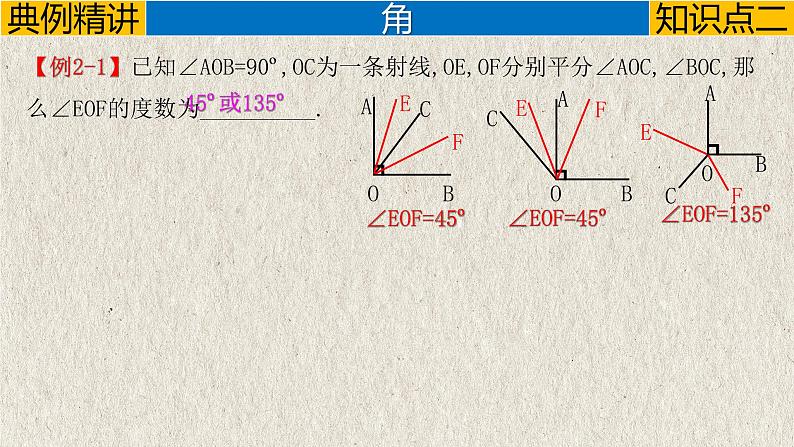
【例2-1】已知∠AOB=90º,OC为一条射线,OE,OF分别平分∠AOC,∠BOC,那么∠EOF的度数为__________.
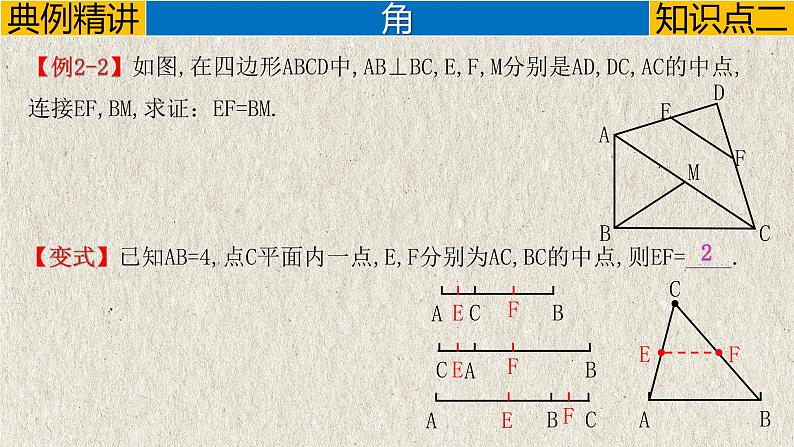
【例2-2】如图,在四边形ABCD中,AB⊥BC,E,F,M分别是AD,DC,AC的中点,连接EF,BM,求证：EF=BM.
【变式】已知AB=4,点C平面内一点,E,F分别为AC,BC的中点,则EF=____.
“折线型”图形求角度时常作的辅助线类型 已知AB∥CD,过点E作EF∥AB,常见图形类型如下表:
∠A+∠C+∠AEC=360º
【例3】(1)如图,∠AOB的一边OA为平面镜,∠AOB=37º45´,在OB边上有一点E,从点E射出一束光线经平面镜反射后,反射光线DC恰好与OB平行,则∠DEB的度数是________________.(2)如图,将木条a,b与c钉在一起,∠1=70º,∠2=50º,要使木条a与b平行,木条a旋转的度数是_____.
75º30´(或75.5º)
【例4】①若a3＞b3,则a2＞b2；②若点A(x1,y1)和点B(x2,y2)在二次函数y=x2-2x-1的图象上,且满足x1＜x2＜1,则y1＞y2＞-2；③在同一平面内,a,b,c是直线,且a∥b,b⊥c,则a∥c；④周长相等的所有等腰直角三角形全等.上述命题中真命题的个数是(　　) A.4个B.3个 C.2个D.1个
1.某同学用剪刀沿直线将一片平整的银杏叶减掉一部分(如图),发现剩下的银杏叶的周长比原银杏叶的周长要小,能正确解释这一现象的数学知识是(　　) A.两点之间线段最短；B.两点确定一条直线；C.垂线段最短；D.经过直线外一点,有且只有一条直线与这条直线平行.2.能说明命题“关于x方程x2-4x+m=0一定有实数根”是假命题的反例( ) A.m=-1 B.m=0 C.m=4 D.m=5 3.判断命题“如果n＜1,那么n2-1＜0”是假命题,只需举出一个反例,反例中的n可以是( ) A.-2 B.-0.5 C.0 D.0.5
4.如图,一把直尺压住射线OB,另一把完全的直尺压住射线OA并且与第一把直尺交于点P,小明说：“射线OP就是∠BOA的角平分线.”他这样做的依据是(　　) A.角的内部到角的两边的距离相等的点在角的平分线上； B.角平分线上的点到这个角两边的距离相等； C.三角形三条角平分线的交点到三条边的距离相等； D.以上均不正确.
5.若∠1=60º,∠2的两边与∠1的两边分别平行,则∠2=___________.6.如图,已知AB∥CD,∠EAB=3∠EAF,∠ECD=3∠ECF,∠AFC=62º,则∠AEC的度数是____.7.如图所示，将含有30º角的三角板的直角顶点放在相互平行的两条直线中的一条上，若∠1=43º，则∠2=_____.
1.如图①,OP为一条拉直的细线,A,B两点在OP上,且OA:AP=1:3,OB:BP=3:5.若先固定B点,将OB折向BP,使得OB重叠在BP上,如图②,再从图②的A点及与A点重叠处一起剪开,使得细线分成三段,则此三段细线由小到大的长度比是(　　) A.1∶1∶1 B.1∶1∶2 C.1∶2∶2 D.1∶2∶52.如图，AE平分∠BAC，BE⊥AE于点E,ED∥AC.若∠BAE=34º,则∠BED的度数为( ) A.134º B.124º C.114º D.104º