



专题复习 -阴影部分面积的计算课件-数学中考一轮复习
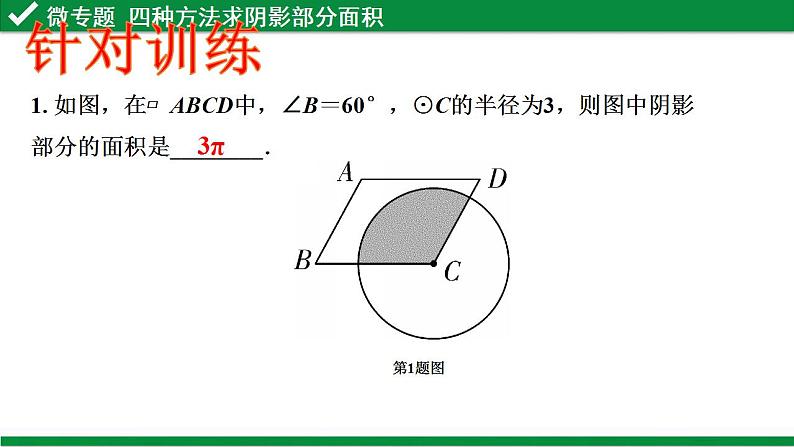
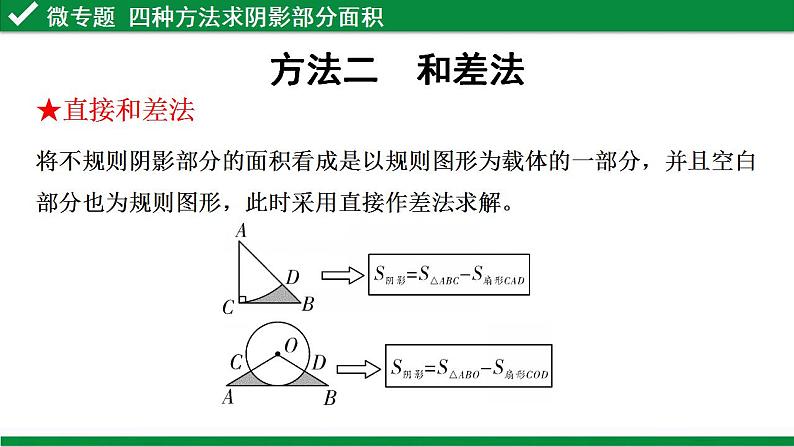
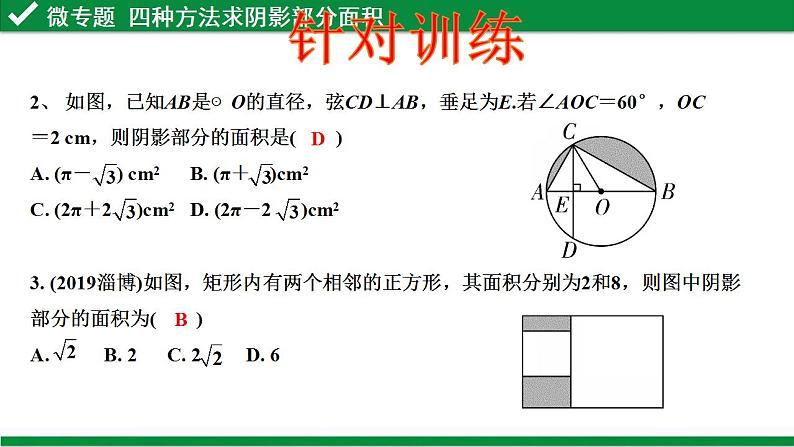
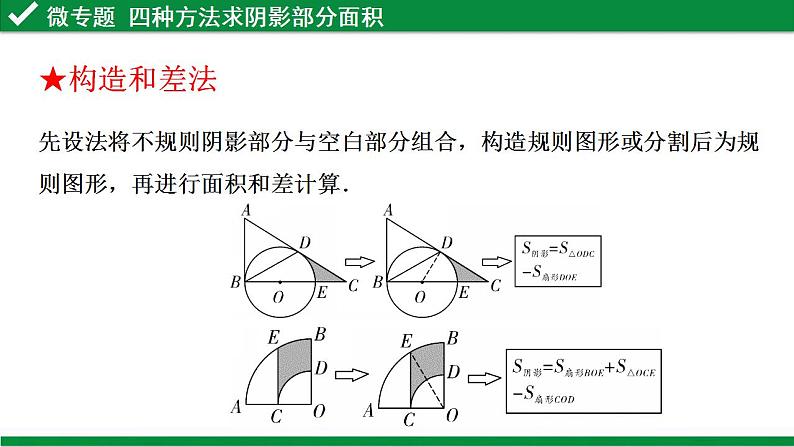
展开【题型解读】近10年考查9次,仅2011年未考查,其考查形式为:①直角三角形结合扇形计算求阴影部分面积考查1次;②扇形与尺规作图结合考查3次;③三角形旋转求阴影部分面积考查2次;④扇形旋转和菱形旋转求阴影部分面积各考查1次;⑤抛物线平移求阴影部分面积考查1次.专题复习----阴影部分面积的计算1、掌握公式法、和差法、等积转化法、容斥原理法等常用方法,将图形适当分割组合,正确求出阴影部分面积。(重点,难点)2、体会“化不规则为规则”的转化思想,在解决阴影部分面积计算中的重要作用。复习目标1、几种面积公式:扇形面积=_______,三角形面积=______,圆面积=______,梯形面积=______,平行四边形面积=______,矩形面积=______,菱形面积=_______,正方形面积=__________等等;2、和三角形有关的知识:如三角形的重心、内心、外心等等;3、和直角三角形相关的知识:如勾股定理,锐角三角函数等等;4、等腰三角形的知识:如“三线合一”,等边三角形的面积等等知识储备方法一 公式法所求阴影部分的面积是规则图形,直接用几何图形的面积公式求解.1. 如图,在▱ABCD中,∠B=60°,⊙C的半径为3,则图中阴影部分的面积是________.第1题图3π 针对训练方法二 和差法将不规则阴影部分的面积看成是以规则图形为载体的一部分,并且空白部分也为规则图形,此时采用直接作差法求解。★直接和差法D2、 如图,已知AB是⊙O的直径,弦CD⊥AB,垂足为E.若∠AOC=60°,OC=2 cm,则阴影部分的面积是( )A. (π- ) cm2 B. (π+ )cm2C. (2π+2 )cm2 D. (2π-2 )cm23. (2019淄博)如图,矩形内有两个相邻的正方形,其面积分别为2和8,则图中阴影部分的面积为( )A. B. 2 C. 2 D. 6针对训练B★构造和差法先设法将不规则阴影部分与空白部分组合,构造规则图形或分割后为规则图形,再进行面积和差计算.第4题图2π-44. 如图,在扇形AOB中,∠AOB=90°,正方形CDEF的顶点C是 的中点,点D在OB上,点E在OB的延长线上.当正方形CDEF的边长为2 时,则阴影部分的面积为________.第5题图5. 如图,两张48×40的矩形纸片有一个顶点重合,重叠放置的尺寸如图所示,则图中阴影部分的面积=________. 984第4题解图第5题解图针对训练方法三 等积转化法通过对图形的变换,为利用公式法或和差法求解创造条件.★直接等面积转化当CD∥AB时.★平移转化法当E、F分别是AB、CD的中点时.★对称转化法当点D是AB的中点时.★旋转转化法第6题图2π 6. 如图,在半径为4的⊙O中,CD是直径,AB是弦,且CD⊥AB,垂足为点E, ∠AOB=90°,则阴影部分的面积是________.第7题图7. 如图,在半径为2 cm的⊙O中,点C、点D是 的三等分点,点E是直径AB延长线上的一点,连接CE、DE,则图中阴影部分的面积是________.针对训练方法四 容斥原理法阴影部分面积是由两个基本图形相互重叠得到的.常用的方法是:“两个基本图形的面积之和”-“被重叠图形的面积”=“组合图形的面积”.8. 如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,以点A为圆心,AC的长为半径作弧CE交AB于点E,以点B为圆心,BC的长为半径作弧CD 交AB于点D,则阴影部分的面积为________.π-2 针对训练S阴影=S扇形CAE+S扇形CBD—S△CAB课堂小结1、掌握求阴影部分面积的4种常用方法------公式 法、和差法、等积转化法、容斥原理法;2、深入体会了转化、化归的数学思想;3、体会到数学的灵活性、多变性,以不变应万变。1. 如图,正六边形的边长为2,分别以正六边形的六条边为直径向外作半圆,与正六边形的外接圆围成的6个月牙形的面积之和(阴影部分面积)是( )A. 6-π B. 6-2πC. 6+π D. 6+2π2. 如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,以BC为直径作半圆,交AB于点D,则阴影部分的面积是( )A. π-1 B. 4-π C. D. 2 AD当堂检测当堂检测3.如图,AB为半圆的直径,且AB=6,将半圆绕点A顺时针旋转60°,点B旋转到点C的位置,则图中阴影部分的面积为________. 4. 如图,四边形ABCD中,AB=CD,AD∥BC,以点B为圆心,BA为半径的圆弧与BC交于点E,四边形AECD是平行四边形,AB=6,则扇形(图中阴影部分)的面积是________.6π6π同学们,再见
中考数学复习重难突破微专题(十二)与圆有关的阴影面积的计算课件: 这是一份中考数学复习重难突破微专题(十二)与圆有关的阴影面积的计算课件,共19页。
数学中考复习小专题: 阴影部分面积课件: 这是一份数学中考复习小专题: 阴影部分面积课件,共16页。PPT课件主要包含了S底×高,三角形面积公式,扇形面积公式,基础公式,2构造和差法,割补法,直击中考等内容,欢迎下载使用。
中考数学复习专项训练五求阴影部分的面积作业课件: 这是一份中考数学复习专项训练五求阴影部分的面积作业课件,共10页。













