

江苏省连云港市海州区2022-2023学年八年级下学期期末数学试题
展开
这是一份江苏省连云港市海州区2022-2023学年八年级下学期期末数学试题,共11页。
2022—2023学年度第二学期期末学业水平质量调研
八年级数学
注意事项:
1.本试卷共6页.全卷满分150分.考试时间为100分钟.考生答题全部答在答题纸上,答在本试卷上无效.
2.作图必须用2B铅笔作答,并请加黑加粗,描写清楚.
一、选择题(本大题共有8题,每小题3分,共24分)
1.下列图形中,是中心对称图形的是( )
A. B. C. D.
2.“抛掷一枚均匀硬币,落地后正面朝上”这一事件是( )
A.必然事件 B.不可能事件 C.随机事件 D.以上都对
3.下列函数是反比例函数的是( )
A. B. C. D.
4.下列计算正确的是( )
A. B.
C. D.
5.若点,都在函数的图像上,则,的大小关系是( )
A. B. C. D.不能确定
6.实数,在数轴上对应点的位置如图所示,化简的结果是( )
A. B. C. D.
7.如图,在中,点、、分别在边、、上,且,.下列四个判断中,不正确的是( )
A.四边形是平行四边形
B.如果,那么四边形是矩形
C.如果平分,那么四边形是矩形
D.如果且,那么四边形是菱形
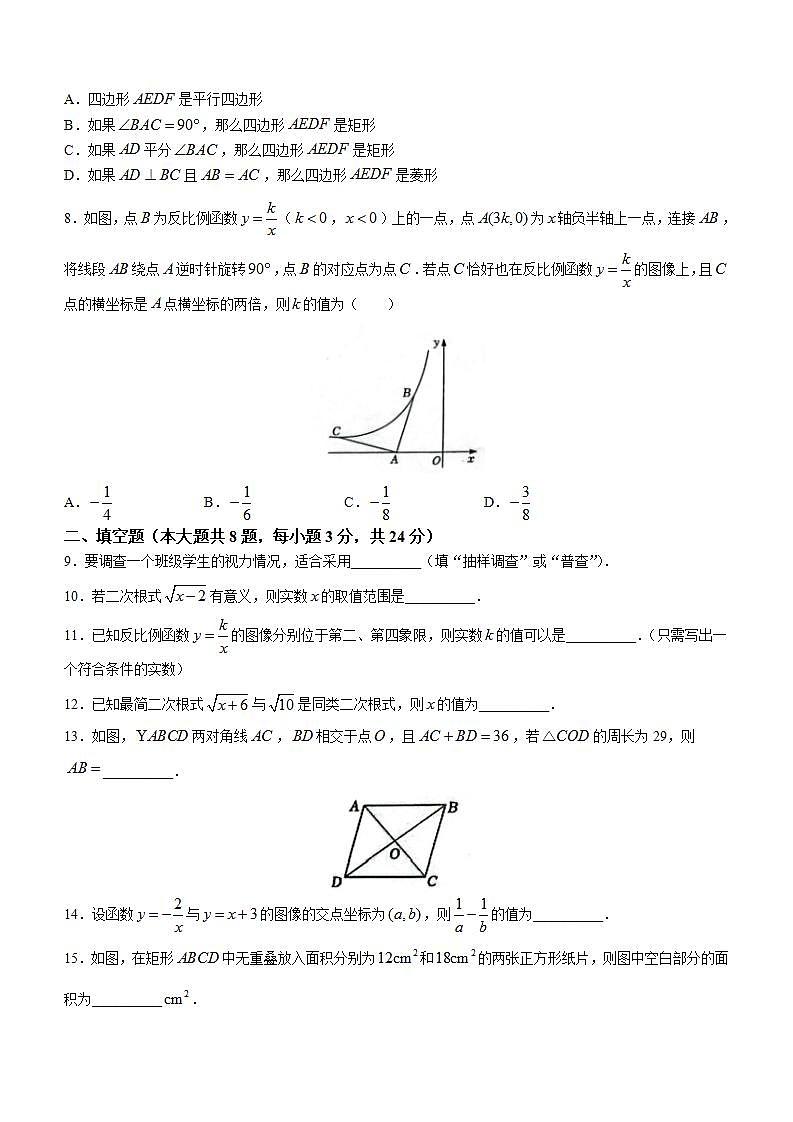
8.如图,点为反比例函数(,)上的一点,点为轴负半轴上一点,连接,将线段绕点逆时针旋转,点的对应点为点.若点恰好也在反比例函数的图像上,且点的横坐标是点横坐标的两倍,则的值为( )
A. B. C. D.
二、填空题(本大题共8题,每小题3分,共24分)
9.要调查一个班级学生的视力情况,适合采用__________(填“抽样调查”或“普查”).
10.若二次根式有意义,则实数的取值范围是__________.
11.已知反比例函数的图像分别位于第二、第四象限,则实数的值可以是__________.(只需写出一个符合条件的实数)
12.已知最简二次根式与是同类二次根式,则的值为__________.
13.如图,两对角线,相交于点,且,若的周长为29,则__________.
14.设函数与的图像的交点坐标为,则的值为__________.
15.如图,在矩形中无重叠放入面积分别为和的两张正方形纸片,则图中空白部分的面积为__________.
16.如图,在中,,,.将绕点按逆时针方向旋转后得,直线、相交于点.取的中点,连接,则长的最大值为__________.
三、解答题(本大题共10题,共102分)
17.(本题共16分)计算与化简:
(1) (2)
(3) (4)
18.(本题共10分)解分式方程:
(1) (2)
19.(本题共8分)密闭容器内有一定质量的二氧化碳,当容器的体积(单位:)变化时,气体的密度(单位:)也随之变化.已知密度与体积是反比例函数关系,它的图像如图所示.
(1)求密度与体积的函数关系式;
(2)当时,求的值;
(3)当密闭容器的体积不能超过,直接写出密度的取值范围.
20.(本题共8分)某校组织学生进行“青年大学习”知识竞赛活动,竞赛成绩分为四个等级,根据某班竞赛结果分别制作了条形统计图和扇形统计图.
请根据相关信息,解答下列问题:
(1)该班学生的总数为__________人,并补全条形统计图;
(2)扇形统计图中等级所对应的扇形圆心角度数为__________;
(3)已知全校共400名学生,现选取每班知识竞赛等级的学生参加校级竞赛,请你估算参加校级竞赛的人数.
21.(本题共8分)如图,在平行四边形中,点是边的中点,连接并延长交的延长线于点,连接,.
(1)求证:四边形是平行四边形;
(2)若,且四边形是矩形时,求的度数.
22.(本题共10分)如图,一次函数与反比例函数的图像交于,两点.
(1)求反比例函数和一次函数的解析式;
(2)根据图像直接写出时,的取值范围;
(3)求的面积.
23.(本题共10分)六一儿童节来临之际,某商店用3000元购进一批玩具,很快售完;第二次购进时,每件的进价提高了,同样用3000元购进的数量比第一次少了10件.求第一次每件的进价为多少元?
24.(本题共10分)像,,两个含有二次根式的代数式相乘,积不含有二次根式,我们称这两个代数式互为有理化因式.例如:与,与,与等都是互为有理化因式.进行二次根式计算时,利用有理化因式,可以化去分母中的根号.请完成下列问题:
(1)化简:;
(2)计算:;
(3)比较与的大小,并说明理由.
25.(本题共10分)如图,四边形是平行四边形且点,将平行四边形绕点逆时针旋转得到平行四边形,经过点,点恰好落在轴的正半轴上,若点,在反比例函数的图像上.
(1)证明:是等边三角形,并求的值;
(2)设,,,是双曲线上的四点,,,试判断,的大小,说明理由.
26.(本题共12分)【问题背景】矩形纸片中,,,点在边上,点在边上,将纸片沿折叠,使顶点落在点处.
【初步认识】
(1)如图1,折痕的端点与点重合.
①当时,__________;
②若点恰好在线段上,则的长为__________;
【深入思考】
(2)若点恰好落在边上.
①如图2,过点作交于点,交于点,连接.请根据题意,补全图2并证明四边形是菱形;
②在①的条件下,当时,求的长;
【拓展提升】
(3)如图3,若,连接,若是以为腰的等腰三角形,求的长.
2022—2023学年度第二学期期末学业水平质量调研
八年级数学参考答案及评分建议
一、选择题(每小题3分,满分24分)
题号
1
2
3
4
5
6
7
8
答案
B
C
A
B
A
D
C
B
二、填空题(每题3分,满分24分)
9.普查 10. 11.(答案不唯一,为负数即可) 12.4
13.11 14. 15. 16.
三、解答题(本大题共10题,共102分)
17.(本题共16分)
解:(1)原式
解:(2)原式(每化简对一个得1分)
解:(3)原式
解:(4)原式
18.(本题共10分)
(1)解:(1)去分母得:,解得:,
检验:把代入得:,∴分式方程的解为;
(2)分式方程整理得,
去分母得:,解得:,
检验:把代入得:,∴是增根,所以原方程无解.
19.(本共8分)
解:(1)设密度关于体积的函数解析式为.
∵当时,,∴,∴,∴;
(2)把代入,得,∴;
(3)
20.(本共8分)
(1)40,补全统计图如下:
(2)54;
(3)(名),
答:参加校级竞赛的大约有40名.
21.(本题共8分)
(1)证明:∵四边形是平行四边形,∴,∴,
∵点是边的中点,∴,
在和中,,∴,∴,
又∵,∴四边形是平行四边形;
(2)证明:∵四边形是矩形,∴,∴,∴,
∵四边形是平行四边形,,∴,∴,
∴.
22.(本题共10分)
解:(1)∵,在的图象上,∴,
∴反比例函数的解析式是.∴.
∵,在函数的图像上,∴,解得:.
则一次函数的解析式是.
所以一次函数的解析式是,反比例函数的解析式是;
(2)当或;
(3)∵直线与轴相交于点,∴的坐标是.
∴.
23.(本题共10分)
解:(1)设第一次每件的进价为元,则第二次进价为,
根据题意得:,解得:,
经检验:是方程的解,且符合题意,
答:第一次每件的进价为50元;
24.(本题共10分)
(1)
(2)计算:
(3)比较与的大小,并说明理由.
∵
∴
25.(本题共10分)
(1)证明:∵四边形是平行四边形,∴,∴,
由旋转可知:,,∴,即,
∵,∴,∴是等边三角形.
由题可知,
∵经过点,点,在反比例函数的图像上,
由反比例函数中心对称性,可得,过点作轴重线,垂足为,
∵是等边三角形,∴,,∴
∴.
(2)∵,,∴,
∴,∴,
∵当时,随增大而减小,∴.
26.(本题共12分)
(1)①,②.
(2)解:①证明:∵,∴,
由折叠可知,,,
∴,∴,∴,∴四边形是平行四边形,
∵,∴四边形是菱形;
②解:由折叠可知,∵,,
在中,,∴,∴菱形的边长为,
由折叠可知,,∵,∴,
在中,,∴,
在中,又勾股定理得.
(3)解:由折叠可知,设,则,,
①当时,在中,,∴,∴;
②当时,过点作交于,∴,
由折叠可知,
∵,∴,
∴,∴,∴,
∴,∴,∴;
综上所述:的长为或.
相关试卷
这是一份江苏省连云港市海州区2022-2023学年八年级下学期期末数学试题(解析版),共25页。试卷主要包含了本试卷共6页等内容,欢迎下载使用。
这是一份江苏省连云港市海州区2022-2023学年八年级下学期期末数学试题(含答案),共11页。试卷主要包含了本试卷共6页,下列函数是反比例函数的是,下列计算正确的是,如图,点为反比例函数等内容,欢迎下载使用。
这是一份江苏省连云港市海州区2022-2023学年八年级下学期期末质量调研数学试卷,共14页。









