江西省九江市2022-2023学年九年级下学期期中数学试题

这是一份江西省九江市2022-2023学年九年级下学期期中数学试题，共11页。
2023年江西省初中学业水平芳试模拟试卷
九年级数学
说明：
1．本卷共有六个大题，23个小题，全卷满分120分，考试时间120分钟。
2．本卷分为试题卷和答题卷，答案要求写在答题卷上。
一、选择题（本大题共6小题，每小题3分，共18分）
1．在，0，3，这组数中，最小的数是（ ）
A． B．0 C．3 D．
2．下列计算正确的是（ ）
A． B． C． D．
3．2022年12月27日上午，都昌县举行新材料及智能装备产业园项目开工仪式，都昌新材料与智能装备产业园共有五个项目，总投资195亿元，数据195亿用科学记数法可表示为（ ）
A． B． C． D．
4．某同学各科成绩如图所示，则其成绩的中位数是（ ）

A．75分 B．75.5分 C．76分 D．77分
5．一副直角三角板按如图所示的方式放置（BC与EF重合），将三角板DEF绕点C逆时针旋转（），当时，（ ）

A． B． C． D．
6．已知抛物线与直线（）交于两点（点A在y轴的左侧），则下列说法错误的是（ ）
A． B． C． D．
二、填空题（每小题3分，共18分）
7．的绝对值是___________．
8．分解因式：__________．
9．若方程的两个根，则的值为___________．
10．对于一次函数的图象，无论k为何值，都过一个定点，则这个点的坐标是___________．
11．已知两个边长为的等边三角形ABC与BDE按如图所示的方式放置，且A、B、D在同一条直线上，连接AE，则AE的长为___________．

12．如图，菱形ABCD的边长为10，对角线AC、BD相交于点O，，点P是AD上一点，，Q为BD上一动点，若以A，P，Q为顶点的三角形是等腰三角形，则BQ的长为___________．

三、解答题（本大题共5小题，每小题6分，共30分）
13．（本大题共2小题，每小题3分）
（1）计算：
（2）解不等式：
14．如图，在平行四边形ABCD中，对角线AC、BD相交于点O，，且BD为的平分线，求证：平行四边形ABCD为正方形．

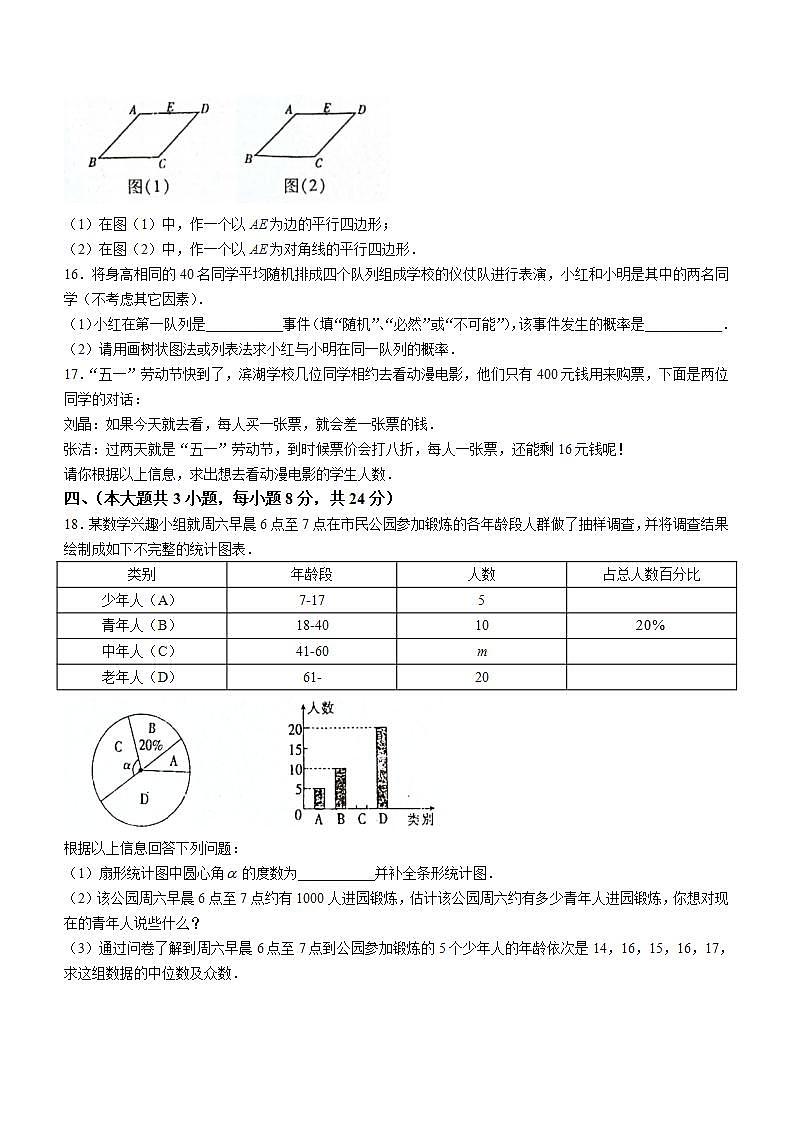
15．如图，已知点E是菱形ABCD的边AD的中点，请仅用无刻度的直尺按下列要求作图．

（1）在图（1）中，作一个以AE为边的平行四边形；
（2）在图（2）中，作一个以AE为对角线的平行四边形．
16．将身高相同的40名同学平均随机排成四个队列组成学校的仪仗队进行表演，小红和小明是其中的两名同学（不考虑其它因素）．
（1）小红在第一队列是___________事件（填“随机”、“必然”或“不可能”），该事件发生的概率是___________．
（2）请用画树状图法或列表法求小红与小明在同一队列的概率．
17．“五一”劳动节快到了，滨湖学校几位同学相约去看动漫电影，他们只有400元钱用来购票，下面是两位同学的对话：
刘晶：如果今天就去看，每人买一张票，就会差一张票的钱．
张洁：过两天就是“五一”劳动节，到时候票价会打八折，每人一张票，还能剩16元钱呢！
请你根据以上信息，求出想去看动漫电影的学生人数．
四、（本大题共3小题，每小题8分，共24分）
18．某数学兴趣小组就周六早晨6点至7点在市民公园参加锻炼的各年龄段人群做了抽样调查，并将调查结果绘制成如下不完整的统计图表．
类别
年龄段
人数
占总人数百分比
少年人（A）
7-17
5

青年人（B）
18-40
10

中年人（C）
41-60
m

老年人（D）
61-
20


根据以上信息回答下列问题：
（1）扇形统计图中圆心角的度数为___________并补全条形统计图．
（2）该公园周六早晨6点至7点约有1000人进园锻炼，估计该公园周六约有多少青年人进园锻炼，你想对现在的青年人说些什么？
（3）通过问卷了解到周六早晨6点至7点到公园参加锻炼的5个少年人的年龄依次是14，16，15，16，17，求这组数据的中位数及众数．
19．如图，已知一次函数与反比例函数的图象交于点，点C在x轴上，为直角三角形，且．

（1）求一次函数与反比例函数的表达式；
（2）求点C的坐标．
20．图1是某校教学楼墙壁上文化长廊中的两幅图案，现将这两个正方形转化为平面图形得到图2，并测得正方形ABCD与正方形EFGH的面积相等，且．

（1）判断四边形CFED的形状，并说明理由．
（2）求CG的长．（参考数据：）
五、（本大题共2小题，每小题9分，共18分）
21．如图，在中，A、B，C三点在上，点O在AD边上，点E在外，，垂足为F．

（1）若，求证：EC是的切线；
（2）若，求AB的长．
22．已知抛物线，若把抛物线的顶点沿直线在第一象限内平行到点（n为非负整数），得到相应的抛物线为，抛物线与y轴的交点为．

（1）若，求抛物线的解析式和点的坐标；
（2）填空：①当时，，的坐标为___________;
②当时，，的坐标为___________;
③根据①、②的结论，写出出的坐标为___________．
（3）过作轴，垂足为B，若是等腰直角三角形，求n的值．
六、（本大题12分）
23．我们定义：如图1，在中，把AB绕点A顺时针旋转（）得到'，把AC绕点A逆时针旋转得到，连接，当时，我们称是的“旋补三角形”，边上的中线AD叫做的“旋补中线”，点A叫做“旋补中心”．特例感知：
（1）在图2，图3中，是的“旋补三角形”，AD是的“旋补中线”．
①如图2，在为等边三角形时，AD与BC的数量关系为___________BC．

②如图3，当时，则AD长为___________．
猜想论证：
（2）在图1中，当为任意三角形时，猜想AD与BC的数量关系，并给予证明．
（3）如图4，在四边形ABCD中，，在四边形内部是否存在点P，使是的“旋补三角形”？若存在，给予证明，并求的“旋补中线”长；若不存在，说明理由．
2023年江西省初中学业水平考试模拟试卷
九年级数学参考答案
一、选择题（共6小题，每小题3分）
1．A 2．C 3．D 4．C 5．B 6．D
二、填空题（共6小题，每小题3分）
7． 8． 9． 10． 11． 12．8，或
三、（本大题共5小题，每小题6分，共30分）
13．（1）原式

3分
（2）

3分
14．证明：四边形ABCD为平行四边行，，O为AC的中点，
又，平行四边形为矩形
为的平分线，，
，∴矩形ABCD为正方形 6分
15．（1）如图（1），平行四边形AFCE即为所求．（答案不唯一） 3分
（2）如图（2），平行四边形AFEG即为所求．（答案不唯一） 6分

16．（1）随机 2分
（2）设四个队列分别为1，2，3，4，根据题意画树状图如下：

由树状图可知，共有16种等可能的结果，其中小红与小明在同一队列的结果有4种．
（小红与小明在同一队列） 6分
17．解：设想去看动漫电影的学生共有x人 1分
根据题意得： 3分
解得： 5分
经检验，是原方程的根且符合题意．
答：想去看动漫电影的学生共6人．
四、（本大题共3小题，每小题8分，共24分）
18．解：（1） ，补图如下：
4分
（2）（人），我想对青年人说，加强锻炼，身体健康比什么都重要！（答案不唯一） 6分
（3）中位数为16，众数为16． 8分
19．（1）将代入反比例函数中，得，解得，
故反比例函数的表达式为 1分
将代入反比例函数中，
得，解得，故 2分
将代入一次函数中得，解得
故一次函数解析式为 4分
（2）如图，

过点A作轴于点D，过点B作轴于点E，
则，
为等腰直角三角形，，
．
在和中，

8分
20．解：（1）四边形CFED是菱形 1分
理由：正方形ABCD与正方形EFGH的面积相等，
，∴四边形CDEF是平行四边形 3分

，
是菱形 5分

（2）作于点M，在中，
，得 7分
8分
五、（本大题共2小题，每小题9分，共18分）
21．（1）证明：连接OB和OC
，

2分

点C在上，是的切线 4分
（2）解：过点F作交OA于点G，，
∴四边形BAGF为平行四边形，
设的半径为x，则

在中，
解得 7分
，
，
∴在中， 9分

22．（1）若，则抛物线的解析式为
令，则有，的坐标为 2分
（2）填空：①；②；③ 5分（每空1分）
（3），

是等腰直角三角形，
①点在B点上方时，，（舍去）
②点在B点下方时，，
此时或，都不合题意， 9分
（第（3）小题4分）
六、（本大题共12分）
23．（1）①，②AD长为9（4分）（每空2分）
（2）猜想 5分
证明：（答案不唯一，供参考）

如图，延长AD至E，使，连接
是的“旋补中线”，．四边形是平行四边形，

由定义可知：，
，
8分
（3）存在 9分

如图，以AD为边向四边形ABCD的内部作等边，连接PB，PC，延长BP交AD于点F
则有，
，
过点P作PE⊥BC于点E，易知四边形PDCE为矩形．

，
又，
，
又，是的“旋补三角形”
，
，
在中，，

在中，
是的“旋补三角形”
的“旋补中线”长为． 12分