北京市第一○一中学2022-2023学年高二下学期期中练习数学试卷

这是一份北京市第一○一中学2022-2023学年高二下学期期中练习数学试卷，共4页。
2023年101中学高二年级第二学期期中练习数  学学校：              班级：              姓名：              成绩：              考生须知本试卷共4页，共三道大题，21道小题，满分150分，考试时间120分钟。在试卷和答题纸上准确填写学校、班级、姓名。试题答案一律填涂或书写在答题纸上，在试卷上作答无效。考试结束，请将本试卷和答题纸一并交回。 第一部分 选择题（共40分）一、选择题。（每小题4分，共40分）1. 已知集合，且，则a可以是A. -1　　　　 B. 0　　　　 C. 1　　　　 D. 22. 若a>0，b>0，lg a+lg b=lg(a+b)，则a+b的最小值为A. 8　　　　 B. 6　　　　 C. 4　　　　 D. 23. 九连环是我国从古至今广为流传的一种益智游戏．在某种玩法中，用an表示解下n(n≤9,且n∈N*)个圆环所需移动的最少次数，{an}满足a1=1，且则解下4个圆环所需的最少移动次数为A. 7　　　　 B. 10　　　　 C. 12　　　　 D. 224. 在四边形ABCD中，AB∥CD，设．若λ+μ=，则=A. 　　　　 B. 　　　　 C. 1　　　　 D. 25. 已知，若，则x0所在区间为A. 　　　 B.   C. 　　　 D. (1,2)6. 已知m,n,p,q为正整数,且m+n=p+q,则在数列{an}中,“am·an=ap·aq”是“{an}是等比数列”的A. 充分而不必要条件　　　　 B. 必要而不充分条件C. 充分必要条件　　　　  D. 既不充分也不必要条件7. 已知A,B,C是椭圆上的三个点，直线AB经过原点O，直线AC经过椭圆的右焦点F，若BF⊥AC，且，则椭圆的离心率是A. 　　　　 B. 　　　 C. 　　　 D. 8. 已知是定义域为(-∞,+∞)的奇函数，满足．若f(1)=2，则f(1)+f(2)+f(3)+…+f(50)=A. 0　　　　 B. 2   C. 50　　　　 D. -509. △ABC的内角A，B，C的对边分别为a，b，c．已知asin A-bsin B=4csin C，cos A=，则=A. 6　　　　 B. 5　　　　 C. 4　　　　 D. 310. 已知函数，下列命题正确的是①是奇函数；②在R上是增函数；③方程有且仅有1个实数根；④如果对任意x∈(0,+∞)，都有f(x)>kx，那么k的最大值为2.A. ①②③  B. ①②④  C. ②③④  D. ①②③④ 第二部分 非选择题（共110分）二、填空题。（每小题5分，共25分）11. 复数z=(1+2i)(3-i)，其中i为虚数单位，则z的实部是　　　　. 12. 设{an}是等差数列，且a1=1，a1+a3=6，则数列{an}的通项公式为　　　　　.13. 若圆与圆相交于A，B两点，且两圆在点A处的切线互相垂直，则线段AB的长度是　　　　.14. 已知函数．若方程f(x)=g(x)有两个不相等的实根，则实数k的取值范围是　　　　. 15. 已知正四面体ABCD，点E为棱AD的中点，O为△BCD的中心，则异面直线EO与CD所成的角等于　　　　.      三、简答题。（共85分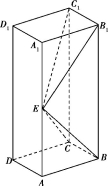）16.（13分）如图，长方体ABCD-A1B1C1D1的底面ABCD是正方形，点E在棱AA1上，BE⊥EC1.（1）证明：BE⊥平面EB1C1；（2）若AE=A1E，求二面角B-EC-C1的正弦值.       17.（13分）在△ABC中，∠A=90°，点D在BC边上．在平面ABC内，过D作DF⊥BC且DF=AC.（1）若D为BC的中点，且△CDF的面积等于△ABC的面积，求∠ABC；（2）若∠ABC=45°，且BD=3CD，求cos∠CFB.      18.（14分）某地区为贯彻习近平总书记关于“绿水青山就是金山银山”的精神，鼓励农户利用荒坡种植果树．某农户考察三种不同的果树苗A、B、C，经引种试验后发现，引种树苗A的自然成活率为0.8，引种树苗B、C的自然成活率均为p(0.7≤p≤0.9).（1）任取树苗A、B、C各一棵，估计自然成活的棵数为X，求X的分布列及E(X)；（2）将（1）中的E(X)取得最大值时p的值作为B种树苗自然成活的概率．该农户决定引种n棵B种树苗，引种后没有自然成活的树苗中有75%的树苗可经过人工栽培技术处理，处理后成活的概率为0.8，其余的树苗不能成活.①求一棵B种树苗最终成活的概率；②若每棵树苗引种最终成活后可获利300元，不成活的每棵亏损50元，该农户为了获利不低于20万元，问至少引种B种树苗多少棵？    19.（15分）已知椭圆过点(2,0)，且椭圆C的离心率为.（1）求椭圆C的方程；（2）若动点P在直线x=-1上，过P作直线交椭圆C于M，N两点，且P为线段MN的中点，再过P作直线l⊥MN，证明：直线l恒过定点，并求出该定点的坐标.       20.（15分）已知函数.（1）求曲线在点(0, f(0))处的切线方程；（2）当a<0时，求证：函数f(x)存在极小值；（3）请直接写出函数f(x)的零点个数.    21.（15分）设和是两个等差数列，记(n=1,2,3,…)，其中max{x1,x2,…,xs}表示x1,x2,…,xs这s个数中最大的数.（1）若an=n，bn=2n-1，求c1，c2，c3的值，并证明{cn}是等差数列；（2）证明：或者对任意正数M，存在正整数m，当n≥m时，；或者存在正整数m，使得cm，cm+1，cm+2，…是等差数列.