初中数学2.1 一元二次方程公开课课件ppt

回顾知识

+

导入新课

回顾知识

+

导入新课

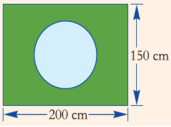
同学们，在上节课中，我们已将学习了有关一元二次方程的概念，而从这节课开始我们将一起开始学习关解一元二次方程的知识，在上新课之前，我们一起回顾下前面学习的有关方程的知识：

 1. 一元二次方程

     ①定义：只含有一个未知数，并且未知数项的最高次数是2的整式方程.

 ②一元二次方程的一般形式：ax2 + bx + c = 0（a、b、c是常数，且a≠0）, a：二次项系数, b：一次项系数，c：常数项。

 2. 方程的解：使方程左右两边相等的未知数的值.

3、什么叫做平方根？平方根有哪些性质？

若x2=a，则x叫做a的平方根.记作：x= ±.

平方根的性质：

(1)一个正数有两个平方根，这两个平方根是互为相反数的；

(2)零的平方根是零； 

(3)负数没有平方根.

接下来，我们看几个例子：

1.如图，已知一矩形的长为200cm，宽150cm.现在矩形中挖去一个圆，使剩余部分的面积为原矩形面积的四分之三.求挖去的圆的半径xcm（其中π取3）.

要建立方程， 关键是找出问题中的等量关系.

等量关系：矩形的面积-圆的面积=矩形的面积×.

解：设由于圆的半径为xcm，则它的面积为 3x2 cm2.

        根据题意得：200×150-3x2 ＝200×150×．

        整理得：x2 - 2500＝0．

那么，如何求解呢？

把方程写成：x2=2500.

这表明 x是2500的平方根，根据平方根的意义，得

x=或 x=        .

因此，原方程的解为：x1=50，x2=－50.圆的半径不可能为负数，所以x2=－50不合题意，应当舍去 .

答：圆的半径为5.cm.

我们可以发现，我们在解题时候用的方法是根据平方根的意义开平方，从而求得方程的解.那这样的方法叫做什么方法呢？

学生跟着教师回忆知识，并思考本节课的知识。

学生思考并回答问题。并跟着教师的讲解思路思考问题，并探究知识。

回顾学过的知识，帮学生复习知识，引出这节课的教学内容，同时也帮助学生能更好的融入课程。

导入新课，利用导入的例子引起学生的注意力。

讲授新课

+

例题讲解

讲授新课

+

例题讲解

像刚刚探究里的解得的x1=50，x2=－50能使方程x2-2500=0左右两边相等.

使方程左右两边相等的未知数的值就是这个一元二次方程的解，一元二次方程的解也叫做一元二次方程的根。

我们看一个具体的例子，再来了解下一元二次方程的解：

【例1】已知x=1是一元二次方程x2-mx+2m=0的一个解，则m的值是 （   A        ） 

  A.-1         B.1      C.0      D.0或1

【解析】∵ x=1是一元二次方程x2-mx+2m=0的一个解

      ∴x=1满足方程x2-mx+2m=0

      ∴把x=1代入方程，得12-m+2=0

        ∴m=-1.

【问题探究】用所学的知识解下列方程，求出x的值，并说明你所用的方法，与同伴交流.

（1）  x2=9

解：根据平方根的意义，得x1=3，x2=-3.

（2）  x2=0

解：根据平方根的意义， 得x1=x2=0.

（3） x2+8=0

解：根据平方根的意义，得  x2=-8，

    ∵负数没有平方根，

    ∴原方程无解.

所用方法：将方程化为x2 = p的形式，根据平方根的意义求解x.

像刚刚的探究里一样，我们可以根据平方根的意义求解一元二次方程的解：

解一元二次方程（1）

1.方法：利用平方根的定义直接开平方求一元二次方程的根的方法叫直接开平方法.

2.具体方法：一般的，将一元二次方程化为x2 = n的形式：

（1）当n>0 时，根据平方根的意义，方程有两个不等的实数根x1=，x2=；

（2）当n=0 时，方程有两个相等的实数根x1=x2=0；

（3）当n<0 时，因为任何实数x，都有x2≥0 ，所以方程无实数根.

我们需要注意的是，能化为x2=n（n≥0）的形式的方程需要具备的特点：

①左边是含有未知数的完全平方式；

②右边是非负常数.

接下来，我们看一个例子，看直接开平方如何求一元二次方程的解：

【例2】解方程：4x²-25=0.：

解：原方程可化为：x2=.

       根据平方根的意义，得x=或 x=  ，

        因此，原方程的根为x1=，x2=.

【总结】解一元二次方程时候，首先将方程化为x2=p的形式，再根据平方根的定义求解.

想一想：问题：当方程为（x+1）2=81时，能否直接开平方求解x的值？

解：∵ （x+1）2=81形如x²=p，

       ∴将x+1看成一个整体

       ∴ x+1=9或 x+1=，也就是把一元二次方程“降次”，转化为两个一元一次方程.

      ∴x=8或x=-10

      因此，原方程的根为x1=8，x2=.

【例3】求解一元二次方程方程（2x+1）2=2.

解：将2x+1看成一个整体，根据平方根的意义，

        得    2x+1= 或2x+1=-

       ∴x=或x=－

        因此，原方程的根为x1=，x2=.

在这里我们对用直接开平方法求解一元二次方程的知识点进行一个小的总结：

1.形如（ax+m）2=n（a、n、m为常数且a≠0）的一元二次方程可用直接开平方法求解x．

2.求解方程：（ax+m）2-n =0（a、m、n为常数，a≠0）

解：将原方程化解为： （ax+m）2=n

根据平方根的意义，得   ax+m= 或ax+m=-

      ①当n<0时，方程无实数解；

      ②当n=0时，x 1 =x2=

      ③当n>0时，x1=，x2=.

结合导入的思考和老师的讲解，利用探究理解和掌握用一元二次方程的解，以及用直接开平方法求一元二次方程的方法。

老师在例题讲解的时候，自己先思考，然后再听老师讲解。

老师在例题讲解的时候，自己先思考，然后再听老师讲解。

结合老师的讲解，利用练习和探究用直接开平方法求一元二次方程的方法。

讲授知识，让学生掌握一元二次方程的解，以及用直接开平方法求一元二次方程的方法。

让学生知道本节课的学习内容和重点。

用例题讲解的方式将知识运用起来，便于学生的理解和记忆。

课堂练习

课堂练习

+

扩展提升

1．一元二次方程x2－9＝0的根为（ C       ）

      A．x＝3　　　　　　　 　 B．x＝－3

      C．x1＝3，x2＝－3  　　　 D．x＝9

2．一元二次方程x2＝14的根是  x 1 =x2　　　．

3 ．若代数式3x²－6的值为21，则x的值是           x1=3，x2=-3         ．

4．解下列方程：

（1）2y2－100＝0；

解：原式化解得：y2=50

         ∴y=±  

         ∴x1=，x2=-.

（2）（x＋6）（x－6）＝64.

解：原式化解得：x2-36=64

       即x2=100

       ∴ x=±10

     ∴x1=10，x2=-10

（3）（x－1）2－4 = 0；

解：移项，得（x-1）2=4.

      ∵x-1是4的平方根，

       ∴x-1=±2.

      ∴x1=3，x2=-1.

（4）12（3－2x）2－3 = 0.

解：移项，得12（3-2x）2=3，

        即（3-2x）2=0.25.

     ∵3-2x是0.25的平方根，

    ∴3-2x=±0.5.

     即3-2x=0.5，3-2x=-0.5

     ∴ x1= ，x2=.

5.已知a是方程 x2+2x－2=0 的一个实数根，  求 2a2+4a+2018的值.

解：由题意得a²+2a-2=0，即a²+2a=2

       ∴2a²+4a+2017= 2（a²+2a）+2018

           =2×2+2018

           =2022

  方法总结：已知解求代数式的值，先把已知解代入，再注意观察，有时需运用到整体思想，求解时，将所求代数式的一部分看作一个整体，再用整体思想代入求值．

学生自主完成巩固练习中的练习，然后在做完之后根据老师的讲解进一步巩固知识。

借助练习，检测学生的知识掌握程度，同时便于学生巩固知识。

课堂小结

在课堂的最后，我们一起来回忆总结我们这节课所学的知识点：

1.一元二次方程的解：使方程左右两边相等的未知数的值，也叫一元二次方程的根.

2.形如（x+m）2=n的一元二次方程可用直接开平方法求解x．

3.求解方程： （x+m）2=n

解： 根据平方根的意义，得x= 或x=-

      ①当n<0时，方程无实数解；

      ②当n=0时，x 1 =x2=

      ③当n>0时，x1=，x2=.

跟着老师回忆知识，并记忆本节课的知识。

帮助学生加强记忆知识。

板书

解一元二次方程（1）

 1.一元二次方程的解：使方程左右两边相等的未知数的值，也叫一元二次方程的根.

2.形如（x+m）2=n的一元二次方程可用直接开平方法求解x．

3.求解方程： （x+m）2=n

解： 根据平方根的意义，得x= 或x=-

      ①当n<0时，方程无实数解；

      ②当n=0时，x 1 =x2=

      ③当n>0时，x1=，x2=.

借助板书，让学生知识本节课的重点。

作业

教材第31页做一做.

教材第31页练习第1、2题.