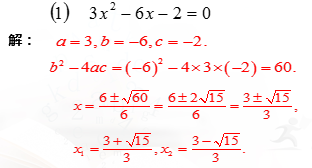数学第2章 一元二次方程2.1 一元二次方程评优课ppt课件
展开新湘教版 数学 九年级上 2.2.2用公式法解一元二次方程教学设计
课题 | 2.2.2用公式法解一元二次方程 | 单元 | 第二单元 | 学科 | 数学 | 年级 | 九年级 |
学习 目标 |
①理解一元二次方程求根公式的推导过程。 ②会用求根公式解简单系数的一元二次方程。
| ||||||
重点 |
| ||||||
难点 |
| ||||||
教学过程 |
教学环节 | 教师活动 | 学生活动 | 设计意图 |
回顾知识 + 导入新课
回顾知识 + 导入新课
| 同学们,在上节课中,我们已将学习了用直接开方的方法、以及配方法解一元二次方程的方法,这节课开始我们将学习一直解一元二次方程的另一种新的方法,在上新课之前,我们一起回顾下前面学习的知识: 用配方法解一元二次方程
【导入新课】运用配方法解一元二次方程时,我们对于每一个具体的方程,都重复使用了一些相同的计算步骤,这启发我们思考:能不能对一般形式的一元二次方程 ax2+bx+c=0(a ≠ 0) 使用配方法,求出这个方程的根呢? 解:化1:把二次项系数化为1
移项:把常数项移到方程的右边
配方:方程两边都加上一次项系数绝对值一半的平方
变形:方程左边分解因式,右边合并同类项;
开方:方程两边开平方; 当 求解:解一元一次方程;
定解:写出原方程的解. x1 ∴ |
学生跟着教师回忆知识,并思考本节课的知识,注意与老师一起推导公式。
学生思考并回答问题。并跟着教师的讲解思路思考问题,并探究知识。 |
回顾学过的知识,帮学生复习知识,引出这节课的教学内容,同时也帮助学生能更好的融入课程。
导入新课,利用导入的例子引起学生的注意力。 |
讲授新课 + 例题讲解
讲授新课 + 例题讲解
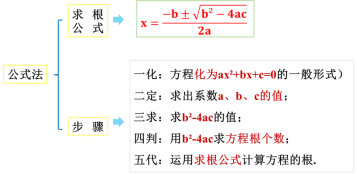
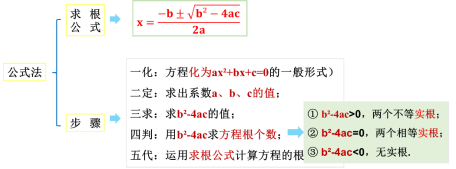
| 一般地,像刚刚推导的一样,一元二次方程ax2+bx+c=0 (a≠0)的根由方程的系数a,b,c确定,当b2-4ac ≥0 时,一元二次方程的根为:
这个式子叫做一元二次方程的求根公式,利用它解一元二次方程的方法叫做公式法. 我们看一个具体的例子,来了解下解一元二次方程: 【例1】用公式法解下列方程: (1)x2 - x –2 = 0. 解:这里 a =1 , b =-1 , c = -2. ∴b2 - 4ac = (-1 )2 - 4×1×(-2 )=9, ∵9>0, ∴ 根据求根公式得x ∴原方程的根为: x1 =2 , x2 = -1. (2)x2 -2 x =1. 解:原式变形成一般式为:x2 -2x-1 =0, 这里 a =1 , b =-2 , c = -1. ∴b2 - 4ac = (-2 )2 - 4×1×(-1 )=8, ∵8>0, ∴ 根据求根公式得x ∴原方程的根为: x1 = 我们可以发现,对于用公式解一元二次方程ax²+bx+c=0(a、b、c均为常数,a≠0)的步骤: 1.变形:化已知方程为一般形式ax²+bx+c=0(a、b、c均为常数,a≠0); 2.确定系数:用a,b,c写出各项系数; 3.计算:计算b²-4ac的值; 4.判断: ①当b²-4ac时,方程有两个不等的实根: ②当b²-4ac时,方程有两个相等的实根: ③当b²-4ac时,因 5.带入求值:利用求根公式求出方程的解. 【例2】用公式法解方程:9x2 +12x+4 =0. 解:这里 a =9 , b =12 , c = 4. ∴ b2 - 4ac = 12 2 - 4×9×4=0, ∴ 根据求根公式得x ∴原方程的根为: x1 =x2 = |
结合导入的思考和老师的讲解,利用探究理解和掌握用用公式求一元二次方程的方法。
老师在例题讲解的时候,自己先思考,然后再听老师讲解。 |
讲授知识,让学生掌掌握用用公式法求一元二次方程的方法。
让学生知道本节课的学习内容和重点。 |
课堂练习
| 1.用公式法解下列方程:
2、对关于x的方程 x2+mx-1=0回答下列问题. (1)m取什么值时,使方程有两个相等的实数根? (2)m取什么值时,方程有两个不等的实数根? (3)m取什么值时,方程有无实数根? 解:这里a=1,b=m,c=-1 ∴b2-4ac =m2-4×1×(-1)=m²+4, ∵从m²+4可以看出,不管m取任意实数, m²+4 >0, ∴不管m取任何的数,方程始终有两个不相等的实数根. 3.已知a,b,c分别是△ABC的三边长,当m>0时,关于x的一元二次方程c(x2+m)+b(x2-m)-2max=0有两个相等的实数根,请判断△ABC的形状. 解:将原方程转为一般形式,得(b+c)x2-2max+(c-b)m2 =0. ∵原方程有两个相等的实数根, ∴(-2ma)2-4(b+c)(c-b)m=0, 即4m2 (a2+b2-c2)=0. 又∵m>0,∴a2+b2-c2=0,即a2+b2=c2. 根据勾股定理的逆定理可知△ABC为直角三角形. |
学生自主完成巩固练习中的练习,然后在做完之后根据老师的讲解进一步巩固知识。
|
借助练习,检测学生的知识掌握程度,同时便于学生巩固知识。
|
课堂小结 | 在课堂的最后,我们一起来回忆总结我们这节课所学的知识点:
| 跟着老师回忆知识,并记忆本节课的知识。 | 帮助学生加强记忆知识。 |
板书 | 用公式法解一元二次方程
| 借助板书,让学生知识本节课的重点。 | |
作业 | 教材第37页练习. 教材第42页练习第4题. | ||
湘教版九年级上册4.2 正切优质课课件ppt: 这是一份湘教版九年级上册4.2 正切优质课课件ppt,文件包含42正切-课件pptx、42正切-试卷docx、42正切-教学设计docx等3份课件配套教学资源,其中PPT共26页, 欢迎下载使用。
初中数学湘教版九年级上册2.2 一元二次方程的解法精品ppt课件: 这是一份初中数学湘教版九年级上册2.2 一元二次方程的解法精品ppt课件,共19页。PPT课件主要包含了情境导入,新课探究,对于方程,把方程的左边配方得,根据平方根的意义得,用公式法解下列方程,解2移项得,课堂练习,解3移项得,解4整理得等内容,欢迎下载使用。
初中数学湘教版九年级上册2.2 一元二次方程的解法教学课件ppt: 这是一份初中数学湘教版九年级上册2.2 一元二次方程的解法教学课件ppt,文件包含湘教版数学九年级上册222公式法pptx、222公式法doc等2份课件配套教学资源,其中PPT共18页, 欢迎下载使用。