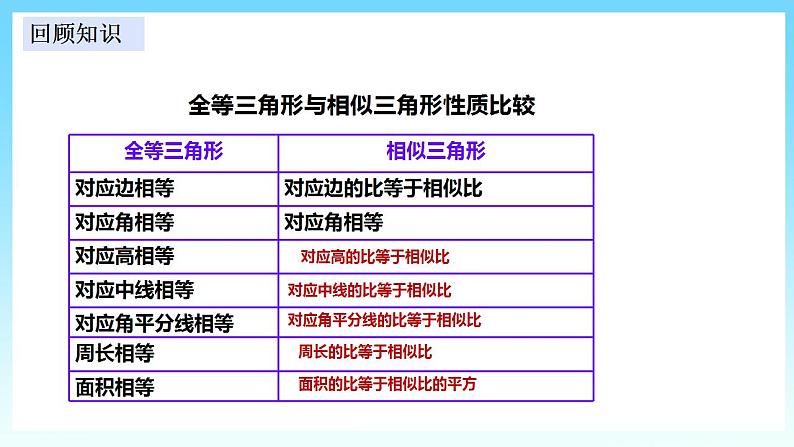
初中数学湘教版九年级上册3.5 相似三角形的应用优质ppt课件

回顾知识

+

导入新课

在前面的学习中，我们已经知道关角形的相似的判定方法以及相似三角形的相关性质。今天，我们将一起学习相似三角形在生活中的应用。在上新课之前，我们一起回顾下之前学过的知识：

1.在池塘外取一点C，使它可以直接看到A，B两点;

2.连接并延长AC，BC;

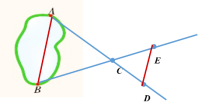
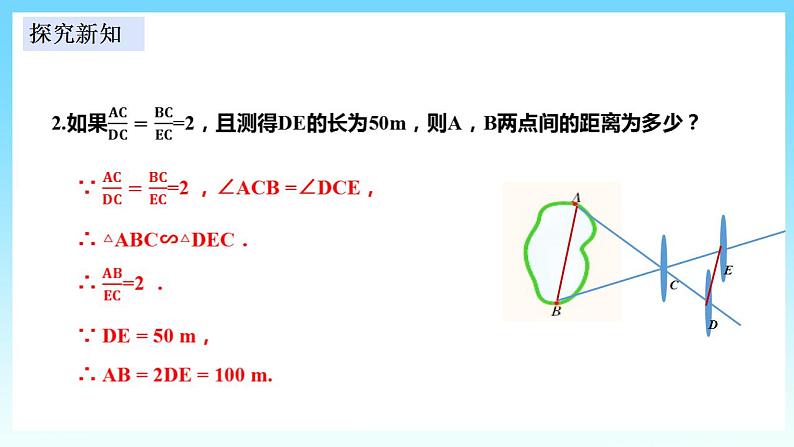
3.在AC的延长线上取一点D， 在BC的延长线上取一点E，

使（k为正整数）

4.测量出DE的长度.

由相似三角形的有关知识

求出A，B两点间的距离.

2.如果=2，且测得DE的长为50m，则A，B两点间的距离为多少？

∵ =2 ，∠ACB =∠DCE，

∴ △ABC∽△DEC．

∴ =2 ．

∵ DE = 50 m，

∴ AB = 2DE = 100 m.

学生思考并回答问题。并跟着教师的讲解思路思考问题，并探究知识。

导入新课，利用导入的例子引起学生的注意力。

讲授新课

+

例题讲解

讲授新课

+

例题讲解

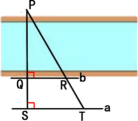
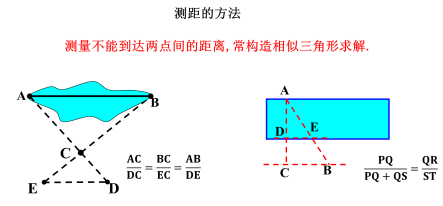
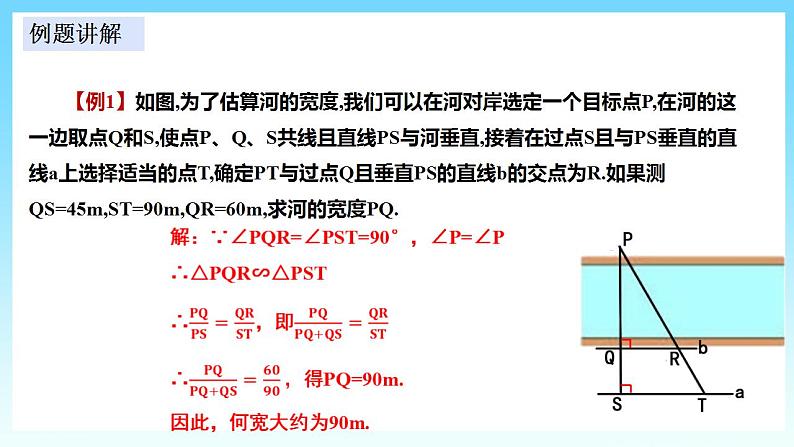
从刚刚导入新课的探究中，我们可以得到两个三角形相似的应用过程中，我们解题的步骤：

利用三角形相似解决实际问题的一般步骤：

（1）根据题意画出___示意图___;

（2）将题目中的已知量或已知关系转化为示意图中的

           _______已知线段、已知角__;

（3）利用相似三角形建立线段之间的关系，求出___未知量_;

（4）写出_____答案___.

接下来，我们看一些具体的例子：

【例1】如图,为了估算河的宽度,我们可以在河对岸选定一个目标点P,在河的这一边取点Q和S,使点P、Q、S共线且直线PS与河垂直,接着在过点S且与PS垂直的直线a上选择适当的点T,确定PT与过点Q且垂直PS的直线b的交点为R.如果测QS=45m,ST=90m,QR=60m,求河的宽度PQ.

解：∵∠PQR=∠PST=90°，∠P=∠P

∴△PQR∽△PST

∴，即

∴得PQ=90m.

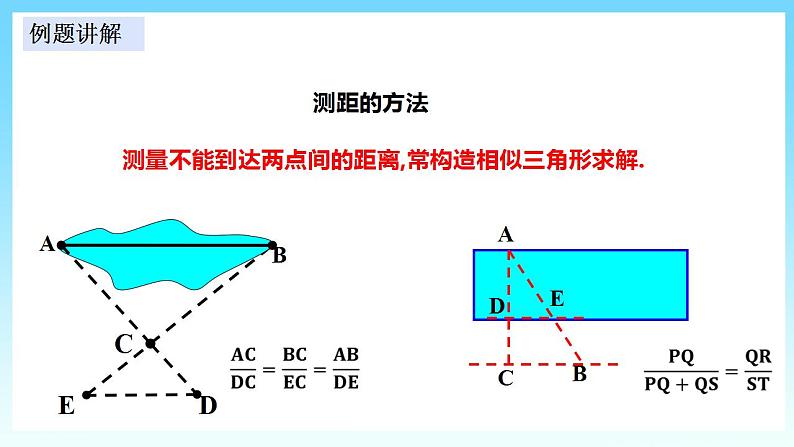
因此，何宽大约为90m.

测距的方法

测量不能到达两点间的距离,常构造相似三角形求解.

【例2】在用步枪瞄准靶心时，要使眼睛（O）、准星（A）、靶心点（B）在同一条直线上.在射击时，李明由于有轻微的抖动，致使准星A偏离到A′，如图所示.已知OA=0.2m，OB=50m，AA′=0.0005m，求李明射击到的点B′偏离靶心点B的长度BB′（近似地认为AA′∥BB′）.  

如何入手？

推出△OAA′∽△OBB′，

利用对应边成比例可得BB′的长度

解：∵ AA′∥BB′，

∴ △OAA′∽△OBB′．

∴                    ．

∵ OA=0.2m，OB=50m，AA′=0.000 5m，

∴ BB′=0.125m.

答：李明射击到的点B′偏离靶心点B的长度BB′为0.125m.

【例3】如图，小明为了测量一棵树CD的高度，他在距树24m处立了一根高为2m的标杆EF，然后小明前后调整自己的位置，当他与树相距27m的时候，他的眼睛、标杆的顶端和树的顶端在同一条直线上.已知小明的眼高1.6m，求树的高度.

如何入手？

分析：人、树、标杆是相互平行的，添加辅助线，过点A作AN∥BD交ID于N，交EF于M，则可得△AEM∽△ACN.

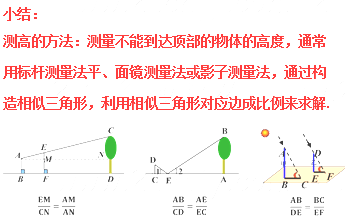
解：过点A作AN∥BD交CD于N，交EF于M，因为人、标杆、树都垂直于地面，

∴∠ABF=∠EFD=∠CDF=90°,

∴AB∥EF∥CD,  ∴∠EMA=∠CNA.

∵∠EAM=∠CAN,

∴△AEM∽△ACN ,

∴.

∵AB=1.6m , EF=2m , BD=27m , FD=24m ,

∴, ∴CN=3.6m，∴CD=3.6+1.6=5.2（m）.

故树的高度为5.2m.

测高的方法

方法1：

测量不能到达顶部的物体高度，可以用“利用标杆测量高度”的原理解决.

【例4】为了测量一棵大树的高度，某同学利用手边的工具（镜子、皮尺）设计了如下测量方案：如图，①在距离树AB底部15m的E处放下镜子；②该同学站在距离镜子1.2m的C处，目高CD为1.5m；③观察镜面，恰好看到树的顶端.

你能帮助他计算出大树的大约高度吗？

解：∵∠1=∠2,∠DCE=∠BAE=90°,

∴△DCE∽△BAE.

∴ ，即得 BA=18.75m.

因此，树高约为18.75m.

测高的方法

方法2：

测量不能到达顶部的物体高度，“利用镜子的反射测量高度”的原理解决.

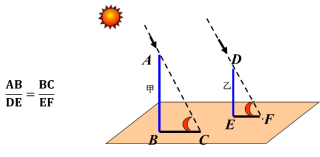
【例5】已知同一时刻物体的高度与影长成正比，在某一时刻，测得一高为4.5米的竹竿的影长为7.2米，某一高楼的影长为36米,那么高楼的高度是多少米?

解：设高楼的高度为x米，则

解得x=22.5.

答:大楼高22.5米.

测高的方法

方法3：

测量不能到达顶部的物体高度，利用“在同一时刻物高与影长成正比例”的原理解决.

结合导入的思考和老师的讲解，利用探究理解和掌握成三角形相似的应用。

老师在例题讲解的时候，自己先思考，然后再听老师讲解。

老师在例题讲解的时候，自己先思考，然后再听老师讲解。

讲授知识，让学生掌掌握三角形相似的应用。

让学生知道本节课的学习内容和重点。

让学生知道本节课的学习内容和重点。

课堂练习

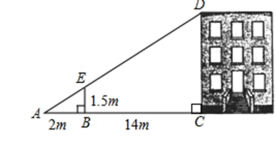
   1.如图，利用标杆BE测量建筑物的高度，标杆BE高1.5m，测得AB=2m，BC=14cm，则楼高CD为多少m．

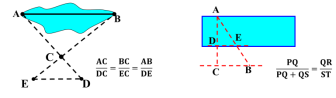
解：∵EB⊥AC，DC⊥AC，

∴EB∥DC，

∴△ABE∽△ACD，∴

∵BE=1.5，AB=2，BC=14，
∴AC=16

∴，∴CD=12．

2.大运河的两岸有一段是平行的，为了估算其运河的宽度，我们可以在对岸选定一个目标作为点A，再在运河的这一边选点B、C，使AB⊥BC，然后再选点E，使EC⊥BC，用视线确定BC和AE的交点为D.如果测得BD=120m，DC=60m，EC=50m，求出大运河的大致宽度AB.

解：∵∠ADB=∠EDC，∠ABC=∠ECD=90°                      ∴△ABD∽△ECD                      

 ∴解得AB=

答：大运河的大致宽度AB是100m.

  3．某同学想利用树影测量树高.他在某一时刻测得小树高为1.5米时，其影长为1.2米，当他测量教学楼旁的一棵大树影长时，因大树靠近教学楼，有一部分影子在墙上.经测量，地面部分影长为6.4米，墙上影长为1.4米，那么这棵大树高多少米?

解：延长AD交地面于E，则

即CE=1.12

∴BE=BC+CE=6.4+1.12=7.52米.

∴即AB=9.4米.

学生自主完课堂练习中的练习，然后在做完之后根据老师的讲解进一步巩固知识。

借助练习，检测学生的知识掌握程度，同时便于学生巩固知识。

课堂小结

在课堂的最后，我们一起来回忆总结我们这节课所学的知识点：

跟着老师回忆知识，并记忆本节课的知识。

帮助学生加强记忆知识。

板书

相似三角形的应用

借助板书，让学生知识本节课的重点。

作业

教材第92页练习第1题. 

 教材第93页练习第2题、习题3.5第1、2题. .