


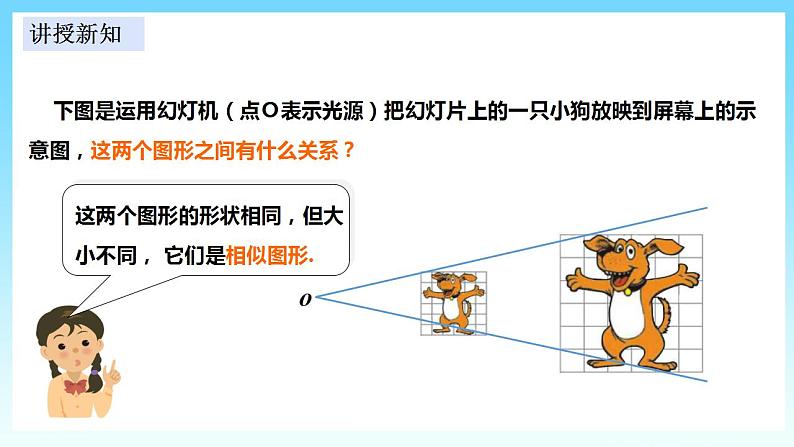
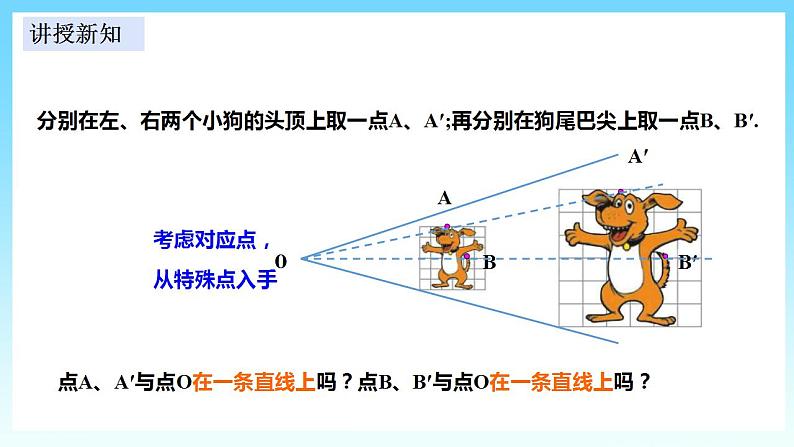


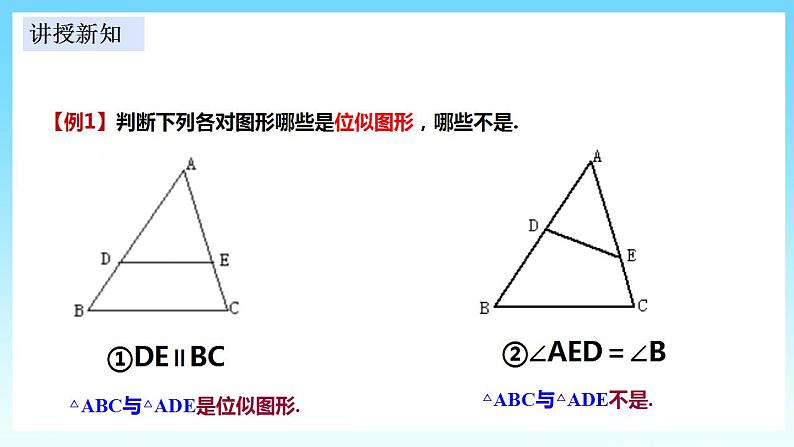






初中数学湘教版九年级上册3.6 位似获奖ppt课件
展开3.6.1 位似
班级:___________姓名:___________得分:__________
(满分:100分,考试时间:40分钟)
一.选择题(共5小题,每题6分)
1.下列图形中△ABC∽△DEF,则这两个三角形不是位似图形的是( )
A.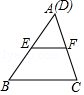 B.
B.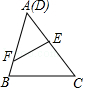
C.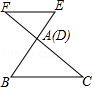 D.
D.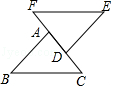
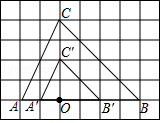
2.如图,在正方形网格中,△ABC和△DEF相似,则关于位似中心与相似比叙述正确的是( )
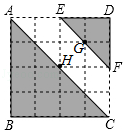
A.位似中心是点B,相似比是2:1
B.位似中心是点D,相似比是2:1
C.位似中心在点G,H之间,相似比为2:1
D.位似中心在点G,H之间,相似比为1:2
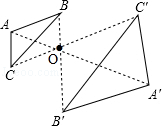
3.如图,以点O为位似中心,将△ABC缩小后得到△A′B′C′,已知BB′=2OB′,则△A′B′C′与△ABC的面积之比( )
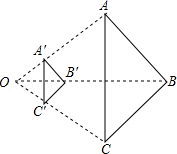
A.1:3 B.1:4 C.1:5 D.1:9
4.如图,以点O为位似中心,将△ABC放大后得到△DEF,已知△ABC与△DEF的面积比为1:9,则AB:DE的值为( )
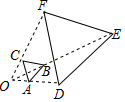
A.1:3 B.1:2 C.1:![]() D.1:9
D.1:9
5.如图,已知△ABC,任取一点O,连接AO,BO,CO,并取它们的中点D,E,F,得△DEF,则下列说法正确的个数是( )
①△ABC与△DEF是位似图形; ②△ABC与△DEF是相似图形;
③△ABC与△DEF的周长比为1:2; ④△若△ABC的面积为4,则△DEF的面积为1
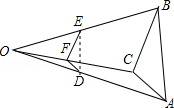
A.1个 B.2个 C.3个 D.4个
二.填空题(共5小题,每题6分)
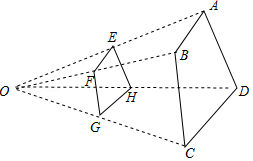
6.如图,已知△EFH和△MNK是位似图形,那么其位似中心是点 (填A、B、C、D).
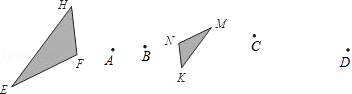
7.如图,△OAB与△OCD是以点O为位似中心的位似图形,点B在OD上,AE、CB分别是△OAB、△OCD的中线,则AE:CB的值为

8.如图,四边形ABCD与四边形EFGH位似,其位似中心为点O,且![]() =
=![]() ,则
,则![]() = .
= .
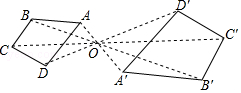
9.如图,四边形ABCD和A'B'C'D'是以点O为位似中心的位似图形,若OA:OA'=2:3,则四边形ABCD与四边形A'B'C'D'的面积比为 .
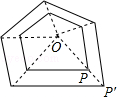
10.如图,如果两个相似多边形任意一组对应顶点P、P′所在的直线都经过同一点O,且有OP′=k•OP(k≠0),那么我们把这样的两个多边形叫位似多边形,点O叫做位似中心.已知△ABC与△A′B′C′是关于点O的位似三角形,OA′=3OA,则△ABC与△A′B′C′的周长之比是 .
三.解答题(共3小题,第11、12题每题10,第13题20分)
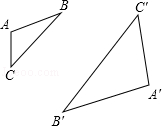 11.如图,△ABC与△A′B′C′是位似图形,且位似比是1:2.
11.如图,△ABC与△A′B′C′是位似图形,且位似比是1:2.
(1)请在图中画出位似中心;
(2)若AB=2cm,则A′B′等于多少?
12.如图,在6×8网格图中,每个小正方形边长均为1,点O和△ABC的顶点均在小正方形的格点上.
(1)以O为位似中心,在网格图中作△A′B′C′,使△A′B′C′和△ABC位似,且相似比为1:2;
(2)连接(1)中的BB′,CC′,求四边形BB′C′C的周长.(结果保留根号)
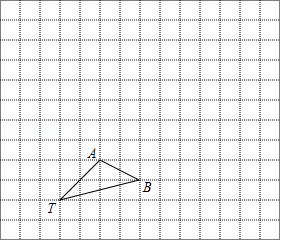
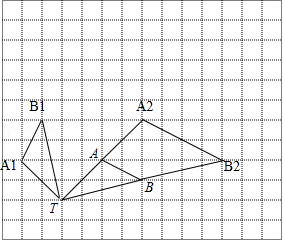
13.如图,在12×12的正方形网格中,△TAB的顶点都在格点处.
(1)把△TAB绕着点T逆时针旋转90°得到△TA1B1.
(2)以T为位似中心,按1:2将△TAB放大,画出放大的△TA2B2(只画一个即可).
试题解析
一.选择题
 2.【分析】在正方形网格中,△ABC和△DEF相似,连接AF,CE,即可得到位似中心在点G,H之间,相似比为2:1.
2.【分析】在正方形网格中,△ABC和△DEF相似,连接AF,CE,即可得到位似中心在点G,H之间,相似比为2:1.
【解答】解:如图,在正方形网格中,△ABC和△DEF相似,连接AF,CE,
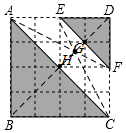
∴位似中心在点G,H之间,
又∵AC=2EF,
∴相似比为2:1,
故选:C.
【点评】本题考查了正方形的性质、位似图形,如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心.
3.【分析】直接根据题意得出位似比,进而得出面积比.
【解答】解:∵以点O为位似中心,将△ABC缩小后得到△A′B′C′,BB′=2OB′,
∴OB′=![]() OB,
OB,
∴△A′B′C′与△ABC的面积之比为:1:9.
故选:D.
【点评】此题主要考查了位似图形的性质,正确得出位似比是解题关键.
4.【分析】利用位似的性质和相似三角形的性质得到![]() ,然后利用比例性质可求出即可.
,然后利用比例性质可求出即可.
【解答】解:∵△ABC与△DEF位似,
∴![]() =
=![]() ,
,
∴![]() ,
,
故选:A.
【点评】本题考查了位似变换:如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心.注意:①两个图形必须是相似形;②对应点的连线都经过同一点;③对应边平行.
5.【分析】根据位似图形的性质,得出①△ABC与△DEF是位似图形进而根据位似图形一定是相似图形得出 ②△ABC与△DEF是相似图形,再根据周长比等于位似比,以及根据面积比等于相似比的平方,即可得出答案.
【解答】解:根据位似性质得出①△ABC与△DEF是位似图形,
②△ABC与△DEF是相似图形,
∵将△ABC的三边缩小的原来的![]() ,
,
∴△ABC与△DEF的周长比为2:1,
故③选项错误,
根据面积比等于相似比的平方,
∴④△ABC与△DEF的面积比为4:1.
故选:C.
【点评】此题主要考查了位似图形的性质,正确的记忆位似图形性质是解决问题的关键.
二.填空题
6.【分析】此题考查位似中心的含义,位似图形对应点连线的交点是位似中心.
【解答】解:如图
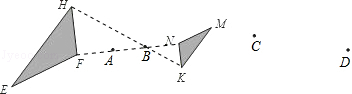
∵△EFH和△MNK是位似图形,连接FN,HK交于点B,故点B是位似中心.
【点评】熟练掌握位似中心的判定.
7.【分析】由,△OAB与△OCD是以点O为位似中心的位似图形,得出相似比解答即可.
【解答】解:∵,△OAB与△OCD是以点O为位似中心的位似图形,
又∵AE、CB分别是△OAB、△OCD的中线,
∴相似比是![]() ,
,
∴AE:CB=1:2,
故答案为:1:2
【点评】此题主要考查了位似变换的性质,正确理解位似与相似的关系进行解答.
8.【分析】直接利用位似图形的性质结合位似比等于相似比得出答案.
【解答】解:∵四边形ABCD与四边形EFGH位似,其位似中心为点O,且![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
则![]() =
=![]() =
=![]() .
.
故答案为:![]() .
.
【点评】此题主要考查了位似变换,正确掌握位似图形的性质是解题关键.
9.【分析】根据两个图形是相似形,根据相似图形的性质:面积之比等于对应边之比的平方可得到答案.
【解答】解:∵四边形ABCD和A'B'C'D'是以点O为位似中心的位似图形,OA:OA'=2:3,
∴四边形ABCD与四边形A'B'C'D'的面积比4:9,
故答案为:4:9.
【点评】此题主要考查了位似变换,关键是掌握相似图形的性质.
10.【分析】根据相似三角形的周长比等于相似比解答.
【解答】解:∵△ABC与△A′B′C′是关于点O的位似三角形,
∴△ABC∽△A′B′C′,
∵OA′=3OA,
∴△ABC与△A′B′C′的周长之比是:OA:OA′=1:3,
故答案为:1:3.
【点评】本题考查的是位似变换的性质,位似变换的性质:①两个图形必须是相似形;②对应点的连线都经过同一点;③对应边平行.
三.解答题
11.【分析】(1)作三组对应点所在直线,三直线的交点即为位似中心O;
(2)根据△ABC与△A′B′C′是位似图形,可知△ABC∽△A′B′C′,利用位似比是1:2,即可求得A′B′=4cm.
【解答】解:(1)如图所示,点O即为位似中心;
(2)∵![]() =
=![]() =
=![]() ,且AB=2cm,
,且AB=2cm,
∴A′B′=2AB=4cm.
【点评】本题考查了位似的相关知识,位似是相似的特殊形式,位似比等于相似比.
12.【分析】(1)直接利用位似图形的性质得出对应点位置进而得出答案;
(2)利用勾股定理得出各线段长,进而得出答案.
【解答】解:(1)如图所示:△A′B′C′,即为所求;
(2)四边形BB′C′C的周长为:
BB′+B′C′+CC′+BC=2+2![]() +2+4
+2+4![]()
=4+6![]() .
.
【点评】此题主要考查了位似变换,正确得出对应点位置是解题关键.
13.【分析】(1)利用旋转的性质画出图形即可;
(2)利用位似图形的性质得出对应点位置进而得出答案;
【解答】解:(1)如图所示:△TA1B1即为所求:
(2)如图所示:△TA2B2即为所求.
【点评】此题主要考查了位似变换,正确得出对应点位置是解题关键.
湘教版九年级上册3.6 位似教课内容ppt课件: 这是一份湘教版九年级上册3.6 位似教课内容ppt课件,共12页。PPT课件主要包含了位似图形的特征,1是相似图形,位似图形的性质,议一议,由题目条件定位置,线段CD就是所求,△DEF就是所求,作位似图形的方法,2找关键点,4写出结论等内容,欢迎下载使用。
湘教版九年级上册第3章 图形的相似3.6 位似优秀课件ppt: 这是一份湘教版九年级上册第3章 图形的相似3.6 位似优秀课件ppt,文件包含362位似-课件pptx、362位似-试卷docx、362位似-教学设计docx等3份课件配套教学资源,其中PPT共20页, 欢迎下载使用。
初中数学湘教版九年级上册3.6 位似精品教学ppt课件: 这是一份初中数学湘教版九年级上册3.6 位似精品教学ppt课件,文件包含湘教版数学九年级上册361位似图形的概念及画法pptx、第1课时位似图形的概念及画法doc等2份课件配套教学资源,其中PPT共12页, 欢迎下载使用。













