初中数学湘教版九年级上册1.1 反比例函数获奖教案设计

回顾知识

+

导入新课

同学们，在上节课中我们已将学习了有关反比例函数的概念和k>0时候的性质，今天我们将进一步走进反比例函数的性质。接下来，我们一起回顾下前面学习知识：

当k<0时候，反比例函数的图象是什么样子呢？具有怎样的性质？下面，我们进行一些探究：

    在同一个直角坐标系中画出反比例函y=-图象与y=的图象.根据题意回答问题.

    ①列表：

    ②描点：

    ③连线：

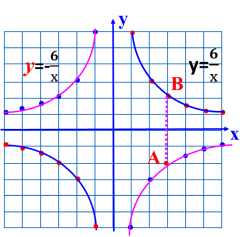
2.如何画反比例函数y=-的图象？与y=的图象有什么关系？

（1）在直角坐标系内描出点 A(3，-2)，B(3，2)，点A与点B有什么关系？

当x=3时，y=-的函数值为－2，而y=的函数值为2.

结论：由于x轴是线段AB的垂直平分线，因此点A与点B关于x轴对称.

（2） y=-图象与y=的图象有什么关系？如何画y=-的图象？

   根据（1）的经验，x取任一非零实数a时，都有点P(a， )与点Q(a，)关于x轴对称，因此y=的图象与y=的图象关于x轴对称.

   于是只要把y=的图象沿着x轴翻折并将图象“复印”下来，就得到y=-的图象.

3.观察y=-的图象，根据y=性质试说出y=-的性质.

图象：y=-的图象由两支曲线（即双曲线）组成，它们与x轴、y轴都不相交.

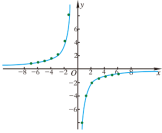
图象增减性：

当x＜0时，函数值随自变量取值的增大而增大；

当x＞0时，函数值随自变量取值的增大而增大.

当k＜0时，反比例函数y=具有与y=-一样的性质.

学生跟着教师回忆知识，并思考本节课的知识。

学生思考并回答问题。并跟着教师的讲解思路思考问题，并探究知识。

回顾学过的知识，帮学生复习知识，引出这节课的教学内容，同时也帮助学生能更好的融入课程。

导入新课，利用导入的例子引起学生的注意力。

讲授新课

+

例题讲解

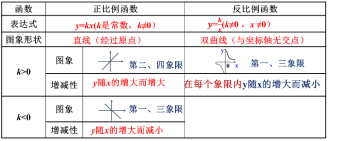
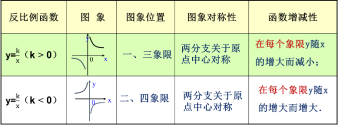
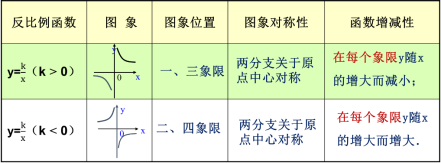
通过刚刚的问题，我们可以得到当k<0时候，反比例函数的性质：

反比例函数y= （k<0）的图象有以下特征：

    一般地，当k<0时，反比例函y=k/x的图象由分别在第二、四象限的双曲线组成，它们与x轴、y轴都不相交，双曲线关于原点成中心对称.

   在每个象限内，函数值y随自变量x的增大而减小.

   我们一起总结下，关于反比例函数的性质：

     1.当k>0时，在图像所在的每一个象限内，y随x的增大而减小；当k<0时，在图像所在的每一个象限内，y随x的增大而增大；

    2.双曲线的两个分支无限接近x轴和y轴，但永远不会与x轴和y轴相交；

3.图象的两个分支关于原点成中心对称.

【例题】画反比例函数y=的图象.

1.列表：

2.描点：以表中各组对应值作为点的坐标，在平面直角坐标系内描出相应的点.

3.连线：用光滑的曲线顺次连接各点,就可得到图象.

结合导入的思考和老师的讲解，利用探究理解和掌握成反比例函数的图象和性质。

老师在例题讲解的时候，自己先思考，然后再听老师讲解。

讲授知识，让学生知道本节课的学习内容和重点。

用例题讲解的方式将知识运用起来，便于学生的理解和记忆。

课堂练习+扩展提高

课堂练习+扩展提高

1.反比例函数y=-的图象大致是（     D       ）

 2.若双曲线y =  的两个分支分别在第二、四象限，则 k 的取值范围是(  B  )

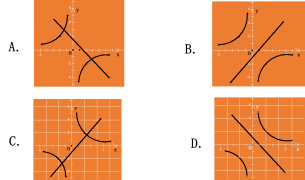
 A. k＞0.5    B. k＜0.5

 C. k=0.5    D.不存在

解析：反比例函数图象的两个分支分别在第二、四象限，则必有2k-1＜0，解得k＜0.5.故选B.

3.点(2，y1)和(3，y2)在函数y =-上，则y1    <   y2．（填“>”、“<”或“=”）

解析：由题意知该反比例函数位于第二、四象限，且y随着自变量x的增大而增大，故y1<y2．

4.下列关于反比例函数y =-的三个结论： 

(1)它的图象经过点（-1，12）和点（10，-1.4）；

(2)它的图象在每一个象限内，y随x的增大而减小； 

(3)它的图象在二、四象限内.

其中正确的是    （1）、（3）     （填序号）．

【扩展提高】如图，函数和y=－kx+1(k>0)在同一坐标系内的图象大致是（ D  ）

K>0:反比例函数图象在第一、三象限.一次函数：递减函数.D正确.

K<0:反比例函数：图象在第二、四象限.一次函数：递增函数.

【做一做】反比例函数y=与一次函数y=kx+k，其中k≠0，则他们的图象可能是（B）

学生自主完成巩固练习中的练习，然后在做完之后根据老师的讲解进一步巩固知识。

学生自主完成巩固练习中的练习，然后在做完之后根据老师的讲解进一步巩固知识。

借助练习，检测学生的知识掌握程度，同时便于学生巩固知识。

借助练习，检测学生的知识掌握程度，同时便于学生巩固知识。

课堂小结

在课堂的最后，我们一起来回忆总结我们这节课所学的知识点：反比例函数的图象与性质

跟着老师回忆知识，并记忆本节课的知识。

帮助学生加强记忆知识。

板书

反比例函数的图形和性质

借助板书，让学生知识本节课的重点。

作业

教材第9页练习.

教材第12页练习1.2第3题.

教材第13页练习1.2第7题.