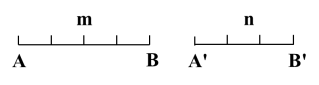数学九年级上册3.1 比例线段优秀教案

回顾知识

+

导入新课

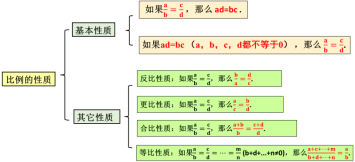
同学们，在上节课中，我们已经学习了有关比例的基本性质，在这节课中，我们将一起学习有关成比例线段的知识。在学习新课之前，我们一起学习下之前的知识：

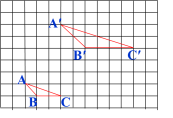
【导入新课】如图， 在方格纸上(设小方格边长为单位1)有△ ABC与△ A′B′C′，它们的顶点都在格点上.试求出线段 AB，BC，AC，A′B′，B′C′，A′C′的长度，并计算AB与A′B′，BC与B′C′，AC与A′C′的长度的比值.

AB=，BC=2，

A′B′=2，B′C′=4...

=0.5 =0.5

它们的比值都为0.5.

学生跟着教师回忆知识，并思考本节课的知识。

学生思考并回答问题。并跟着教师的讲解思路思考问题，并探究知识。

导入新课，利用导入的例子引起学生的注意力。

讲授新课

+

例题讲解

讲授新课

+

例题讲解

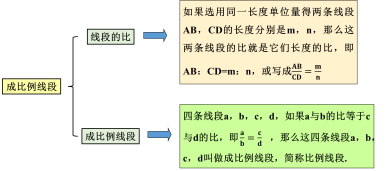
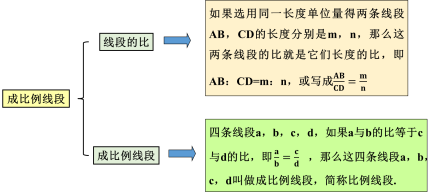
从刚刚导入新课的探究中，我们可以得到两条线段的比：

   如果选用同一个长度单位得两条先线段AB，A'B'的长度分别是m ， n，那么这两条线段的比就是它们长度的比，即

AB:A'B'= m : n 或    

如果把表示成比值k，那么=k，或AB=k · A'B'，两条线段的比实际上就是两个数的比.

  成比例线段：在四条线段中，如果其中两条线段的比等于另外两条线段的比，那么这四条线段叫作成比例线段，简称比例线段.

例如，已知四条线段a，b， c，d，若 ，则a，b， c，d是比例线段.

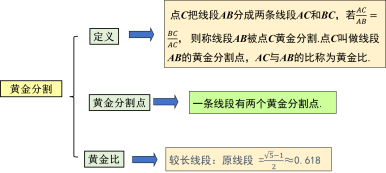
  2.如果作为比例内项的是两条相同的线段 ，即，或 a：b=b：c，那么线段 b 叫做线段 a 和 c 的比例中项.

三种不同形式：①  ②a：b=b：c ③b2=ac.

接下来，我们看一些具体的例子：

【例1】已知线段 a，b，c，d 的长度分别为0.8 cm，2 cm，1.2 cm，3 cm，问 a，b，c，d 是比例线段吗？

解：∵0.4， 0.4

 ∴， ∴a，b，c，d 是比例线段.

【例2】判断下列线段a、b、c、d是否是成比例线段：　

（1）a＝2，b＝6，c＝3，d＝10；

解：∵

 ∴

∴a，b，c，d 不是比例线段.

（2）a＝2，b＝，c＝d=3

解：∵

  ∴

  ∴a，b，c，d 是比例线段.

线段的比与成比例线段的异同

相同：都是线段的长度的比；

不相同：（1）数量上：线段的比是2条线段，成比例线段是4条线段.（2）形式上：成比例线段可写成“比例式”，而线段的比是等式.

问题：度量C到点A、B的距离， 能使与相等吗？

  点C把线段AB分成两条线段AC和BC，如果， 那么称线段AB被点C黄金分割.点C叫做线段AB的黄金分割点，AC与AB的比称为黄金比.

计算黄金比:

解：由，得AC2 = AB·BC.

        设AB = 1，AC = x，则BC = 1 – x.

      ∴  x2 = 1 ×（1 - x）.

即      x2 + x – 1 = 0.

解方程得：x1= 、 x2=.

黄金比≈0.618

【例3】在设计人体雕像时，使雕像的上部（腰以上）与下部（腰以下）的高度比，等于下部与全部（全身）的高度比，可以增加视觉美感．按此比例，如果雕像的高为2m，那么它的下部应设计为多高？

解：设雕像的下部高为x m，则题意得：

整理得：x2+2x﹣4=0，

解得x1=﹣1，x2=﹣﹣1（舍去），

答：雕像的下部高为﹣1 m．

接下来，我们欣赏下黄金分割的魅力：

雕塑－－维纳斯：人的俊美，体现在头部及躯干是否符合黄金分割. 美神维纳斯，她身体的各个部位都暗藏比例0.618，虽然雕像残缺，却能仍让人叹服她不可言喻的美．

结合导入的思考和老师的讲解，利用探究理解和掌握成比例线段。

老师在例题讲解的时候，自己先思考，然后再听老师讲解。

老师在例题讲解的时候，自己先思考，然后再听老师讲解。

讲授知识，让学生掌掌握成比例线段。

让学生知道本节课的学习内容和重点。

例题讲解利于学生对知识的巩固和运用，能让学生知道本节课的学习内容和重点。

综合扩展

+

课堂练习

综合扩展

+

课堂练习

 1.下列各组数中一定成比例的是(    B     )

   A.2，3，6，9             B.-2，4，-4，8

   C.-2， 3，   2，9        D.a，2m，c，2d

 2.已知一个比例式的比例外项为m，n，比例内项为a，b，则下面所给的比例式正确的是(   D     )

    A. m：n=a：b           B.m：b=n：a.

C.m：a=n：b              D.m：a=b：n.

3.已知，AB=15，AC=10，BD=6．求AE．

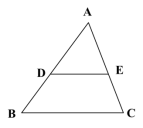
解：根据题意可知，，

        AB = 15 ， AC = 10 ， BD = 6.

       则      AD = AB –  BD =15 – 6= 9.

       则AE=10=6

  4.已知线段a=10mm ， b=6cm， c=2cm ， d=3cm.

  （1）问：这四条线段是否成比例？为什么?

答：这四条线段成比例.

∵a=10mm=1cm

∴ ，，∴

∴线段a、c、d、b成比例.

（2）想一想: 是否还可以写出其他几组成比例的线段.

答:可以.如：、等.

5.点C是线段AB的黄金分割点，如果AB=4，求线段 AC的长度．

AC=4×0.618=2.472

AC=4×（1-0.618）=1.518

  6.小明家搬进了新房，他买了一幅山水画，想挂到书房（书房高3米），请你帮他设计一下，挂在多高能给人赏心悦目的感觉？

离地面的高度 h=3×0.618=1.854m

【综合扩展】1.地图上的比例尺，表示图上距离比实际距离缩小的程度，因此也叫缩尺.

    用公式表示为：比例尺=.

 2.比例尺通常有三种表示方法.

 ①数字式：用数字的比例式或分数式表示比例尺的大小，例如地图上1厘米代表实地距离500千米，可写成：1∶50 000 000.

 ②线段式：在地图上画一条线段，并注明地图上1厘米所代表的实际距离.

 ③文字式：用文字直接写出地图上1厘米代表实地距离多少千米.

【做一做】1.在1 : 500000的地图上，若A、B两市的距离是64cm则两个城市间的实际距离是多少千米？

解：设A、B两市距离为x cm，则

      ∴x=64×500000=32000000(cm)=320(km).

        答：两城市实际距离为320千米

   2. 图3-8是天坛公园的平面图，图中的1 cm代表实际度的220 m.

（1）此平面图的比例尺.答：1：22000.

（2）从最南边的昭亨门到北天门的实际距离是多少米？

答：1892 m.

 （3）用AB，CD分别表示图3-8中西天门与东天门的连线段，昭亨门与北天门的连线段，求．

答：

学生自主完课堂练习中的练习，然后在做完之后根据老师的讲解进一步巩固知识。

综合扩展时候，学生运用自己所学的知识去解决问题，然后听老师讲解，做一做的时候运用扩展的知识去解决问题。

综合扩展有利于学习对知识的灵活运用，利于学生对知识的扩展综合。

借助练习，检测学生的知识掌握程度，同时便于学生巩固知识。

借助练习、做一做等检测学生的知识掌握程度，同时便于学生巩固知识。

课堂小结

在课堂的最后，我们一起来回忆总结我们这节课所学的知识点：

跟着老师回忆知识，并记忆本节课的知识。

帮助学生加强记忆知识。

板书

比例的基本性质

借助板书，让学生知识本节课的重点。

作业

教材第66页练习第1、2题.

教材第67页练习3.1第3、4、6题.