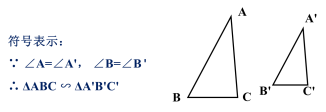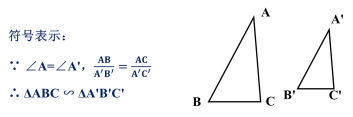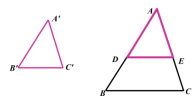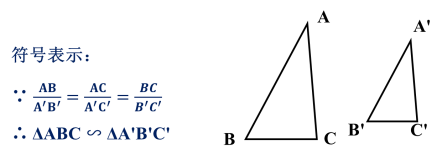初中数学3.4 相似三角形的判定与性质公开课教学设计

回顾知识

+

导入新课

在前面的学习中，我们已经知道有段两个三角形全等的判定定理，同样的对与三角形的相似也有许多的判定方法，在前面的课中我们已经学过判定三角形相似3种方法，今天我们将继续探究其他的方法。在上新课之前，我们一起回顾下之前学过的知识：

    平行于三角形一边的直线与其他两边相交，截得的三角形与原三角形相似．

相似三角形的判定定理1 ：

如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似.

（两角分别相等的两个三角形相似）

相似三角形的判定定理2 ：

      如果一个三角形的两条边与另一个三角形的两条边对应成比例，且夹角相等，那么这两个三角形相似．（两边对应成比例且夹角相等的两个三角形相似.）

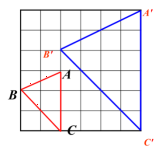
【导入新课】如图,方格纸上画两个三角形，使△ABC的边长是△A’B’C’ 的.

（1）量一量∠A与∠A’，∠B与∠B’ ，∠C与∠C’ 的大小，他们分别相等吗？

.

（2）这两个三角形相似吗？由此你发现什么规律？

两个三角形相似.

学生思考并回答问题。并跟着教师的讲解思路思考问题，并探究知识。

导入新课，利用导入的例子引起学生的注意力。

讲授新课

+

例题讲解

讲授新课

+

例题讲解

从刚刚导入新课的探究中，我们可以得到两个三角形相似的判定定理3：

   如果一个三角形的三条边与另一个三角形的三条边对应成比例，那么这两个三角形相似．（三边对应成比例的两个三角形相似.）

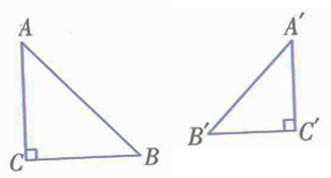
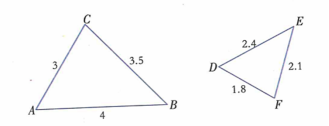
证明：

如图，在△ABC 和△ A’B’C’中，已知=K.求证:ΔABC∽ △ A'B'C‘.

证明:在△ABC的边AB上截取AD=A′B′, 过点D作DE∥BC交AC于点E.

∴ △ADE∽△ABC，∴ =.

∵AD=A’B’, ,

∴,

∴AE=A’C’,DE=B’C’

∴△ADE ≌ △A’B’C’

∴△ABC ∽△A’B’C’

【小试牛刀】 已知△ABC和 △DEF，根据下列条件判断它们是否相似.

(1)  AB=3，    BC=4，    AC＝6

    DE＝6，  EF＝8，   DF＝9

(2) AB=4，    BC=8，    AC＝10

     DE＝20，  EF＝16，   DF＝8

(3)  AB=12，   BC=15，    AC＝24

      DE＝16，  EF＝20，   DF＝30

解：（1）否，（2）是，（3）否.

结论：（大对大，小对小，中对中）

接下来，我们看一些具体的例子：

【例1】在Rt △ ABC和Rt△A'B'C'中， ∠C=90°， ∠C’= 90， .  求证: Rt△ABC∽Rt △ A 'B'C'.

分析:已知两边成比例，只要得到三边成比例即可完成证明.

【例2】判断图中的两个三角形是否相似，并说明理由，

解：在△ABC中，AB> BC>CA，在△DEF中，DE>EF> FD.

∵，，=.

∴=

∴△DEF∽△ABC.

小结：

【做一做】1.两个直角三角形一定相似吗？
  两个等腰直角三角形呢？为什么？

1.所有的直角三角形不都相似；

2.所有的等腰直角三角形都相似.

2、两个等腰三角形一定相似吗？
      两个等边三角形呢？为什么？

1.所有的等腰三角形不都相似；

2.所有的等边三角形都相似.

结合导入的思考和老师的讲解，利用探究理解和掌握成两个三角形相似的判定定理3。

老师在例题讲解的时候，自己先思考，然后再听老师讲解。

老师在例题讲解的时候，自己先思考，然后再听老师讲解。

讲授知识，让学生掌握两个三角形相似的判定定理3。

让学生知道本节课的学习内容和重点。

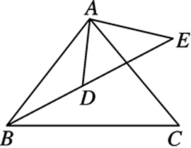
1、已知ABC的三边长分别为6cm，7.5cm，9cm，△DEF的一边长为4cm，当△DEF的另两边长是下列哪一组时，这两个三角形相似         （              C   ）   

A. 2cm，3cm；            B. 4cm，5cm；

C. 5cm，6cm；            D. 6cm，7cm .

  2．若△ABC各边分别为AB＝5cm，BC＝4cm，AC＝3cm，△DEF的两边分别为DE＝10cm，EF＝8cm，则当DF＝　        6      cm时，△ABC∽△DEF.

   3．在Rt△ABC与Rt△A′B′C′中，∠C＝∠C′＝90°，AB＝13cm，AC＝12cm，A′B′＝19.5cm，当A′C′＝　 18      　cm时，Rt△ABC∽Rt△A′B′C′.             

4．如图，已知＝＝，∠BAD＝22°.求∠CAE的度数．

解：∵＝＝，

∴△ABC∽△ADE，

∴∠BAC＝∠DAE，

∴∠BAD＝∠CAE，

∵∠BAD＝22°，

∴∠CAE＝22°.

学生自主完课堂练习中的练习，然后在做完之后根据老师的讲解进一步巩固知识。

借助练习，检测学生的知识掌握程度，同时便于学生巩固知识。

课堂小结

在课堂的最后，我们一起来回忆总结我们这节课所学的知识点：

  相似三角形的判定定理3 ：

如果一个三角形的三条边与另一个三角形的三条边对应成比例，那么这两个三角形相似．（三边对应成比例的两个三角形相似.）

板书

两个三角形相似（4）

相似三角形的判定定理3 ：

如果一个三角形的三条边与另一个三角形的三条边对应成比例，那么这两个三角形相似．（三边对应成比例的两个三角形相似.）

借助板书，让学生知识本节课的重点。

作业

教材第85页练习第1、2题.