湘教版九年级上册3.4 相似三角形的判定与性质优秀教案

回顾知识

+

导入新课

在前面的学习中，我们已经知道有关两个三角形相似的判定方法，而今天我们将学习有关两个三角形相似的性质。在上新课之前，我们一起回顾下之前学过的知识：

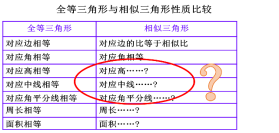
 同时，我们在前面的学习之中已经学习过有关全等三角形的性质，以及部分的有关相似三角形的性质，我们一起看：

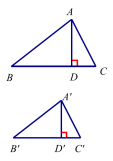
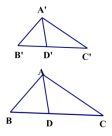
【导入新课】接下来，我们一起来看个问题：

问题：如图,△A’B’C’ ∽△ABC，相似比为k，分别作BC，B’C’上的高AD，A’D’ ．那么=吗？

解：∵△ A’B’C’ ∽△ABC，

∴ ∠B′= ∠B．

又∵ △A’D’C’ =∠ADB =90°，

∴△ A’B’D’ ∽△ABD. (两角对应相等两个三角形相似)

∴==k.

类似的，我们可以得到其余两组对应边上高等于相似比k.

学生思考并回答问题。并跟着教师的讲解思路思考问题，并探究知识。

导入新课，利用导入的例子引起学生的注意力。

讲授新课

+

例题讲解

讲授新课

+

例题讲解

讲授新课

+

例题讲解

从刚刚导入新课的探究中，我们可以得到两个三角形相似的性质：

        如果两个三角形相似，那么这两个三角形的对应边上的对应高的比等于相似比．

（相似三角形对应高的比等于相似比.）

符号表示：

∵ ΔABC ∽ ΔA’B’C’，AD、A’D’分别为BC、B’C’边上的高

∴ =k

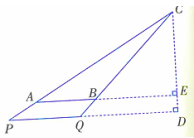
接下来，我们看一些具体的例子：

【例1】如图，AB//PQ，AB=100m，PQ=120m，点P，A，C在一条直线上，点Q，B，C也在一条直线上.若AB与PQ的距离是40m，求点C到直线PQ的距离.

解：∵ AB//PQ，∴△CAB∽CPQ.

过点C作CD⊥PQ，垂足为点D.

设CD交AB的延长线与点E，∴CE⊥AB，DE=40m.

由“相似三角形对应高的比等于相似比”可得，

.

又AB=100m，PQ=120m，DE=40m，

∴CD=240m.

答：点C到直线PQ的距离为240m.

【例2】如图，△A’B’C’∽△ABC， AD，A’D’分别为角平分线. 求证:.

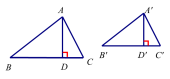
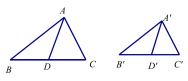
证明∵△ A’B’C’∽△ABC，

∴ ∠B′= ∠B， ∠ A’B’C’ = ∠BAC ．

  又AD，A’D’分别为角平分线

∴∠BAD=BAC=B’A’C’=∠B’A’D

∴△A’B’D’ ∽△ABD.

∴

相似三角形对应角平分线的比等于相似比.

【讲授新课】相似三角形的性质 ：

 如果两个三角形相似，那么这两个三角形的对应角平分线的比等于相似比．

（相似三角形对应角平分线的比等于相似比.）

符号表示：

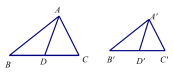
∵ ΔABC ∽ ΔA‘B’C’，AD、A’D’分别为∠BAC和∠B’A’C’边上的高

∴ =k

【知识探究】【议一议】如图，已知△A’B’C’∽△ABC， 若AD，A’D’分别BC、B’C’的中线.则成立吗？由此你能得出什么结论？

证明∵△ A’B’C’∽△ABC，

∴ ∠B′= ∠B， ．

  又AD，A’D’分别BC、B’C’的中线

∴BD=BC，B’C’

∴=

∴△A’B’D’ ∽△ABD.   ∴

相似三角形对应中线的比等于相似比.

【讲授新知】相似三角形的性质 ：

      如果两个三角形相似，那么这两个三角形的对应边上的对应中线的比等于相似比．

（相似三角形对应中线的比等于相似比..）

符号表示：

∵ ΔABC ∽ ΔA‘B’C’，AD、A’D’分别为BC和B’C’边上的中线

∴ =k

【例3】已知△ABC∽△DEF，BG、EH分△ABC和△DEF的角平分线，BC＝6cm,EF＝4cm,BG＝4.8cm.求EH的长.

解：∵ △ABC∽△DEF，

∴（相似三角形对应角平分线的比等于相似比）

即

解得EH=3.2（cm）

答：EH的长为3.2cm. 　

现在我们一起结合全等三角形回顾下本节课的知识：

结合导入的思考和老师的讲解，利用探究理解和掌握两个三角形相似的性质。

老师在例题讲解的时候，自己先思考，然后再听老师讲解。

老师在例题讲解的时候，自己先思考，然后再听老师讲解。

讲授知识，让学生掌掌握两个三角形相似的性质。

让学生知道本节课的学习内容和重点。

让学生知道本节课的学习内容，同时加深对知识的理解和巩固，同时让学生知道本节课的重点。

课堂练习

1.填空：

   2.已知△ABC∽△A‘B’C‘，AD、A ’D ‘分别是对应边BC、B ’C ‘上的高，若BC＝8cm, B ’C ‘＝6cm，AD＝4cm，则A 'D '等于（    C ）

1. 16cm      B.  12 cm                 

C.  3 cm        D.  6 cm

  3．两个相似三角形对应高的比为3∶7，它们的对应角平分线的比为（  D  ）

 A . 7∶3        B.  49∶9    

 C.  9∶49       D. 3∶7 

  4．等腰三角形ABC的腰长为18cm，底边长为6cm，在腰AC上取点D, 使△ABC∽ △BDC，则DC=______.

解： ∵ △ABC∽△BDC

∴

即

∴DC=2cm.

 5．如图，在△ABC中，D、E分别是△ABC的AB、AC边上的点，DE∥BC，CF、EG分别是△ABC与△ADE的中线，已知AD∶DB＝4∶3，AB＝18cm，EG＝4cm，求CF的长．

解：∵AD∶DB＝4∶3，

∴AD∶AB＝4∶7，

∵DE∥BC，

∴△ABC∽△ADE.

∵CF、EG分别是△ABC与△ADE的中线，

∴＝，∴＝，∴CF＝7cm.

学生自主完课堂练习中的练习，然后在做完之后根据老师的讲解进一步巩固知识。

借助练习，检测学生的知识掌握程度，同时便于学生巩固知识。

课堂小结

在课堂的最后，我们一起来回忆总结我们这节课所学的知识点：

相似三角形的性质

1. 对应边的比等于相似比；
2. 对应角相等；
3. 对应高的比等于相似比；
4. 对应中线的比等于相似比
5. 对应角平分线的比等于相似比

跟着老师回忆知识，并记忆本节课的知识。

帮助学生加强记忆知识。

板书

相似三角形的性质

1. 对应边的比等于相似比；
2. 对应角相等；
3. 对应高的比等于相似比；
4. 对应中线的比等于相似比
5. 对应角平分线的比等于相似比

借助板书，让学生知识本节课的重点。

作业

教材第87页练习第1、2题.