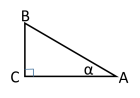湘教版数学九年级上册 4.1.1 正弦-教学设计

回顾知识

+

导入新课

从这节课开始，我们将一起学习有关三角函数的知识。如图是上海东方明珠电视塔的远景图， 你能想办法测量出该塔的高度吗？测量高度或者距离之类的问题，一般可以用本章锐角三角函数的知识来解决．

问题1:画一个直角三角形， 其中一个锐角为65°， 量出65°角的对边长度和斜边长度， 计算               =               ？

 与同桌和邻桌的同学交流， 看看计算出的比值是相等（精确到0.01）的吗？

小明量出∠A的对边BC=3cm，斜边AB=3.3cm，算出：          =         ？

小亮量出∠A’的对边B’C’=2cm，斜边A’B’=2.2cm算出：

           =              ？

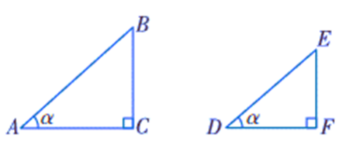
问题2：由问题1猜测：在有一个锐角为65°的所有直角三角形中，65°角的对边与斜边的比值是一个常数，它等于.

这个猜测是真的吗？ 若把65°角换成任意一个锐角α， 则这个角的对边与斜边的比值是否也是一个常数呢？

  你能想办法利用已学的知识证明吗？

   问题3：如图4－2， △ABC 和△DEF 都是直角三角形， 其中∠A＝ ∠D ＝α ， ∠C =∠F = 90°， 则成立吗？ 为什么？

∵ ∠A =∠D =α， ∠C =∠F = 90°，

∴ Rt△ABC∽Rt△DEF.

∴

则

在有一个锐角等于α的所有直角三角形中，角α的对边与斜边的比值是一个常数，与直角三角形的大小无关.

学生思考并回答问题。并跟着教师的讲解思路思考问题，并探究知识。

导入新课，利用导入的例子引起学生的注意力。

讲授新课

+

例题讲解

讲授新课

+

例题讲解

从刚刚导入新课的探究中，我们可以得到正弦的定义：

   正弦的定义：

 在直角三角形中，锐角α的对边与斜边的比值叫作角α的正弦函数，记作 sinα，即

 sinα==.

结合平面直角坐标系求某角的正弦函数值，一般过已知点向x轴或y轴作垂线，构造直角三角形，再结合勾股定理求解.

接下来，我们看一些具体的例子：

【例1】如图4-3，在直角三角形ABC中，∠C=90°，BC=3，AB=5.

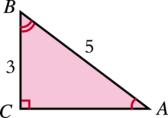
（1）求sinA的值；

解：∠A的对边BC=3，斜边AB=5.于是sinA=.

（2）求sinB的值．

解：∠B的对边AC，根据勾股定理，得

 AC2 = AB2-BC2

            = 52-32 = 16.

于是  AC = 4.

因此sinB=

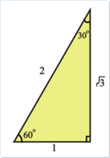
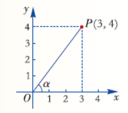
【例2】在直角三角形中，30°角所对的直角边与斜边有什么关系？若设30°角所对的直角边为1，则斜边的值是多少？       

在直角三角形中，30°角所对的直角边等于斜边的一半.

可以得到：sin30°=.

【扩展】如图， 在平面直角坐标系内有一点P（3，4）， 连接OP， 求OP与x轴正方向所夹锐角α 的正弦值.

解： 平面直角坐标系内点P的坐标为（3，4），

连接OP，由勾股定理得 OP=5,

角α的对边是直角边，边长为4，而斜边长OP为5 ，

∴ sin α =

小结：

 sinα=

        1.sina 是在直角三角形中定义的，∠a是锐角.

        2.sina不是sin与a的乘积，而是一个整体，表示∠a的正弦。

        3.sina是线段的一个比值，无单位，注意比的顺序.

        4.sina 的大小只与∠a的大小有关，而与直角三角形的边长无关.

结合导入的思考和老师的讲解，利用探究理解和掌握有关正弦的定义。

老师在例题讲解的时候，自己先思考，然后再听老师讲解。

讲授知识，让学生掌握正弦的定义。

让学生知道本节课的学习内容和重点。

课堂练习

1．在有一个锐角等于α的所有直角三角形中，角α的对边与斜边的比值是一个______常数__，与直角三角形的___大小____无关．

2．如图，在直角三角形中，锐角α的_____对边__与__斜边___的比叫作角α的___正弦____，记作sin α，即sin α＝              .

3．在Rt△ABC中，∠C＝90°，则表示(   B)

A．sin A     B．sin B

C．sin C     D．以上都不对

4．下列说法正确的是(     C   )

A．sin A表示一个角

B．sin A表示sin和A的乘积

C．sin A表示一个比值

D．sin A表示两条线段

5. 如图，在直角三角形ABC中，∠C=90°，BC=6，AB=10.

（1）求sinA的值；

答： sinA

（2）求sinB的值．

答： sinB

 6.已知a，b，c是△ABC的三边，a，b，c满足等式b2＝(c＋a)(c－a)，且5b－4c＝0，求sin A＋sin B的值．

解：1∶b2＝(c＋a)(c－a)，∴b2＝c2－a2，∴a2＋b2＝c2，

∴△ABC是直角三角形，且∠C＝90°.

又∵5b－4c＝0，

∴，则∴sinA+sinB=.

学生自主完课堂练习中的练习，然后在做完之后根据老师的讲解进一步巩固知识。

借助练习，检测学生的知识掌握程度，同时便于学生巩固知识。

课堂小结

在课堂的最后，我们一起来回忆总结我们这节课所学的知识点：

正弦的定义：

 在直角三角形中，锐角α的对边与斜边的比值叫作角α的正弦函数，记作 sinα，即

 sinα==.

跟着老师回忆知识，并记忆本节课的知识。

帮助学生加强记忆知识。

板书

正弦

在直角三角形中，锐角α的对边与斜边的比值叫作角α的正弦函数，记作 sinα，即  sinα==.

借助板书，让学生知识本节课的重点。

作业

教材第111页练习第1、2题.