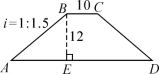
湘教版九年级上册4.3 解直角三角形优质教学设计及反思

回顾知识

+

导入新课

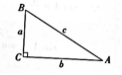
在上节课中，我们已经学习了有关正弦、余弦以及正切的定义，以及特殊角度的正弦、余弦、正切的值。也探究了直角三角形的知识解决与仰角、俯角有关的实际问题，在这节课中，我们将进一步探究有关三角函数的知识。在上新课之前，我们一起回忆下前面学习的知识。

如图，在直角三角形ABC中，∠C=90°，∠A，∠B，∠C的对边分别记作a，b，c .

（1）直角三角形的三边之间有什么关系？

a2+b2=c2(勾股定理)

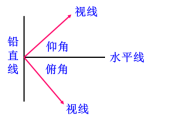
（2）直角三角形的锐角之间有什么关系？ ∠A+∠B=90°.

（3）直角三角形的边和锐角之间有什么关系？

sin A=  cos A= tan A=

从下向上看，视线与水平线的夹角叫做仰角；

从上往下看，视线与水平线的夹角叫做俯角.

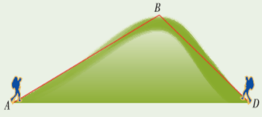
【导入知识】如图，从山脚到山顶有两条路AB与BD， 问哪条路比较陡？右边的路BD陡些．如何用数量来刻画哪条路陡呢？

学生思考并回答问题。并跟着教师的讲解思路思考问题，并探究知识。

导入新课，利用导入的例子引起学生的注意力。

讲授新课

+

例题讲解

从刚刚导入新课的探究中，我们了解到：

坡度：如图，从山坡脚下点A上坡走到点B时，升高的高度h（即线段BC的长度）与水平前进的距离l（即线段AC的长度）的比叫作坡度，又叫坡比，用字母i表示，即i=（坡度通常写成1：m的形式）

坡角：坡面与地平面的夹角α叫坡角．即∠BAC 为坡角．

在图中，∠BAC 为坡角，记作α．

显然，坡度与坡角的关系为：坡度等于坡角的正切，即

i==tanα.可以发现，坡度越大，山坡越陡．

接下来，我们看一些具体的例子：

【例1】如图， 一山坡的坡度为i = 1∶2 . 小刚从山脚A 出发， 沿山坡向上走了240 m 到达点C. 这座山坡的坡角是多少度？ 小刚上升了多少米？ （角度精确到0.01°，长度精确到0.1 m）

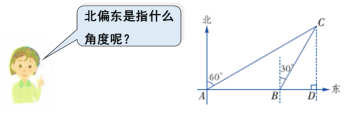
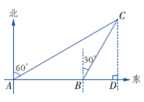
解：用α 表示坡角的大小， 由题意可得：

    tanα==0.5，  因此α ≈26.57°.

    在Rt△ABC中，∠B =90°，∠A = 26.57°， AC =240 ，

因此sin α=得BC = 240 ×sin 26.57°≈107.3（ｍ）．

答：这座山坡的坡角约为26.57°，小刚上升了约107.3 m．

用解直角三角形知识解决此类问题的一般步骤：

（1）通过读题把已知转化为数学图形；

（2）找出直角三角形和已知、未知元素；

（3）选择合适的锐角三角函数求未知数；

（4）解题.

【做一做】如图4-21， 一艘船以40 km/h 的速度向正东航行， 在A 处测得灯塔C 在北偏东60°方向上， 继续航行1 h到达B 处，这时测得灯塔C 在北偏东30°方向上. 已知在灯塔C的四周30 km内有暗礁．问这艘船继续向东航行是否安全？

可以得到：方位角：指北或者指南方

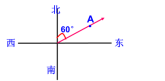
向线与目标方向线所成的小于90°的角叫做方位角.

    如图，点A的方位角为北偏东60°.

【例2】如图4-21， 一艘船以40 km/h 的速度向正东航行， 在A 处测得灯塔C 在北偏东60°方向上， 继续航行1 h到达B 处，这时测得灯塔C 在北偏东30°方向上. 已知在灯塔C的四周30 km内有暗礁．问这艘船继续向东航行是否安全？

 分析：在两个直角三角形中，分别利用300 、 600角的正切，用同一个参量x表示出AD 、 BD的长，进而用方程思想求解.

解：作CD⊥AB， 交AB延长线于点D． 设CD = x.

在Rt△ACD中，∵tan∠CAD=，

∴AD=.

同理，在Rt△BCD中，AD=.

∵AB=AD-BD，∴=40.解得x=20

又20≈34.64>30.

因此，该船能继续安全地向东航行．

结合导入的思考和老师的讲解，利用探究理解和掌握解直角三角形有关坡角、方位角的方法。

老师在例题讲解的时候，自己先思考，然后再听老师讲解。

讲授知识，让学生掌掌握解直角三角形有关坡角、方位角的方法。

让学生知道本节课的学习内容和重点。

课堂练习

课堂练习

1．如图，坡面的铅直高度h和水平宽度l的比叫作坡面的__坡度__，记作i，即i＝___(坡度通常写成___1：m__的形式)．坡面与___水平面___的夹角叫作坡角，记作α.显然坡度等于坡角的___正切 ___，即i＝___＝____tanα ___．坡度越__大____，山坡越陡．

2. 如图，一河坝的横断面为等腰梯形ABCD，坝顶宽10米，坝高12米，斜坡AB的坡度i＝1∶1.5，则坝底AD的长度为(                               D   )

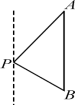
 A．26米     B．28米 

 C．30米     D．46米

 3．如图，一艘海轮位于灯塔P的北偏东30°方向，距离灯塔80海里的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东45°方向上的B处，这时，海轮所在的B处与灯塔P的距离为(    C)

 A．40海里     B．40海里

 C．80海里      D．40海里

 4．如图，某地下车库的入口处有斜坡AB，它的坡度为i＝1∶2，斜坡AB的长为6米，车库的高度为AH(AH⊥BC)，为了让行车更安全，现将斜坡的坡角改造为14°(图中∠ACB＝14°)．

 (1)求车库的高度AH；

解：由题意可得，AH∶BH＝1∶2.

设AH＝x，则BH＝2x，

故x2＋(2x)2＝(6)2，

解得：x＝6.

故车库的高度AH为6 m；

(2)求点B与点C之间的距离．(结果精确到1米)(参考数据：sin 14°≈0.24，cos 14°≈0.97，tan 14°≈0.25)

解：∵AH＝6，∴BH＝2AH＝12，

∴CH＝BC＋BH＝BC＋12.

在Rt△AHC中，∠AHC＝90°，故tan∠ACB＝.

又∵∠ACB＝14°，∴tan14°＝，

∴0.25＝，解得：BC＝12，

故点B与点C之间的距离是12 m.

 5.如图，小明从点A处出发，沿着坡角为α的斜坡向上走了0.65千米到达点B，sin α＝，然后又沿着坡度为i＝1∶4的斜坡向上走了1千米达到点C.问小明从A点到点C上升的高度CD是多少千米？(结果保留根号)

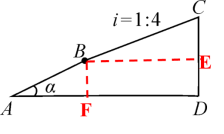
解：过点B作BF⊥AD于点F，过点B作BE⊥CD于点E.

由题意得：AB＝0.65千米，BC＝1千米，

∴sin α＝＝，∴BF＝0.65×＝0.25(km)．

∵斜坡BC的坡度为：1∶4.

∴CE∶BE＝1∶4.

设CE＝x，则BE＝4x，由勾股定理得：x2＋(4x)2＝12，解得：x＝.

∴CD＝CE＋DE＝BF＋CE＝+.

故小明从A点到点C上升的高度CD是（+）km.

学生自主完课堂练习中的练习，然后在做完之后根据老师的讲解进一步巩固知识。

学生自主完课堂练习中的练习，然后在做完之后根据老师的讲解进一步巩固知识。

借助练习，检测学生的知识掌握程度，同时便于学生巩固知识。

借助练习，检测学生的知识掌握程度，同时便于学生巩固知识。

课堂小结

在课堂的最后，我们一起来回忆总结我们这节课所学的知识点：

1.坡度：升高的高度h与水平前进的距离l的比叫作坡度，用字母i表示，即 i==tan α （坡度通常写成l：m的形式）

2.坡角：坡面与地平面的夹角α叫坡角．坡度越大，山坡越陡.

3.方位角：指北或者指南方向线与目标方向线所成的小于90°的角叫做方位角.

跟着老师回忆知识，并记忆本节课的知识。

帮助学生加强记忆知识。

板书

解直角三角形——坡角、方位角

1.坡度：升高的高度h与水平前进的距离l的比叫作坡度，用字母i表示，即 i==tan α （坡度通常写成l：m的形式）

2.坡角：坡面与地平面的夹角α叫坡角．坡度越大，山坡越陡.

3.方位角：指北或者指南方向线与目标方向线所成的小于90°的角叫做方位角.

借助板书，让学生知识本节课的重点。

作业

教材第129页练习第1、2题.