初中数学湘教版九年级上册3.4 相似三角形的判定与性质精品一课一练

3.4.1.3 相似三角形判定定理2

班级：___________姓名：___________得分：__________

（满分：100分，考试时间：40分钟）

一．选择题（共5小题，每题6分）

1．如图，△ABC中，D，E分别是AB，AC上的点，DE∥BC，DE=1，BC=3，AB=6，则AD的长为（　　）

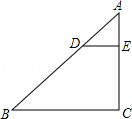
A．1 B．1.5 C．2 D．2.5 

2．如图，小正方形的边长均为1，则下列图中的三角形（阴影部分）与△ABC相似的是（　　）

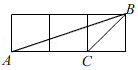
A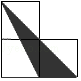． B． 

C． D．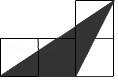 

3．下列条件不能判定△ADB∽△ABC的是（　　）

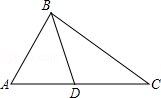
A．∠ABD=∠ACB B．∠ADB=∠ABC 

C．AB2=AD•AC  D．= 

4．如图，点A，B，C，D的坐标分别是（1，7），（1，1），（4，1），（6，1），以C，D，E为顶点的三角形与△ABC相似，则点E的坐标不可能是（　　）

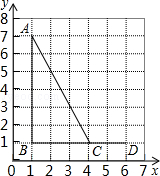
A．（6，0） B．（6，3） C．（6，5） D．（4，2） 

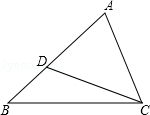
5．如图所示，下列条件中能单独判断△ABC∽△ACD的个数是（　　）个．

①∠ABC=∠ACD；②∠ADC=∠ACB；③=；④AC2=AD•AB

A．1     B．2    C．3    D．4

二．填空题（共5小题，每题6分）

6．在△ABC中，AB=12，AC=9，在AB边上有一点D，AD=4，在AC边上有一动点E．当AE=　   　时，△ABC与△ADE相似．

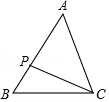
7．如图，P是△ABC的边AB上的一点．（不与A、B重合）当∠ACP=∠　   　时，△APC与△ABC是否相似；当AC、AP、AB满足　   　时，△ACP与△ABC相似．

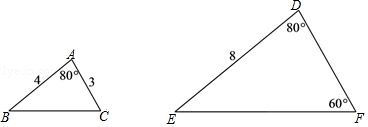
8. 如图标记了△ABC与△DEF边、角的一些数据，如果再添加一个条件使△ABC∽△DEF，那么这个条件可以是　   　．（只填一个即可）

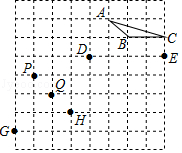
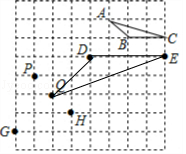
9.图中的每个点（包括△ABC的各个顶点）都在边长为1的小正方形的顶点上，在P、Q、G、H中找一个点，使它与点D、E构成的三角形与△ABC相似，这个点可以是　   　．（写出满足条件的所有的点）

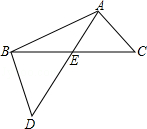
10．如图，点D为△ABC外一点，AD与BC边的交点为E，AE=3，DE=5，BE=4，要使△BDE∽△ACE，且点B，D的对应点为A，C，那么线段CE的长应等于　   　．

三．解答题（共2小题，每题20分）

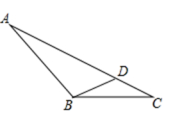
11．如图，在△ABC中，D为AC边上一点，BC=4，AC=8，CD=2．求证：△BCD∽△ACB．

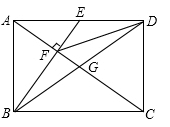
12.如图，在矩形ABCD中，对角线AC、BD相交于点G，E为AD的中点，连接BE交AC于F，连接FD，若∠BFA=90°，求证：△FED∽△DEB．

试题解析

一．选择题

2．【分析】根据正方形的性质求出∠ACB，根据相似三角形的判定定理判断即可．

【解答】解：由正方形的性质可知，∠ACB=180°﹣45°=135°，

A、C、D图形中的钝角都不等于135°，

由勾股定理得，BC=，AC=2，

对应的图形B中的边长分别为1和，

∵=，

∴图B中的三角形（阴影部分）与△ABC相似，

故选：B．

【点评】本题考查的是相似三角形的判定，掌握两组对应边的比相等且夹角对应相等的两个三角形相似是解题的关键．

3．【分析】根据有两个角对应相等的三角形相似，以及根据两边对应成比例且夹角相等的两个三角形相似，分别判断得出即可．

【解答】解：A、∵∠ABD=∠ACB，∠A=∠A，∴△ABC∽△ADB，故此选项不合题意；

B、∵∠ADB=∠ABC，∠A=∠A，∴△ABC∽△ADB，故此选项不合题意；

C、∵AB2=AD•AC，∴=，∠A=∠A，△ABC∽△ADB，故此选项不合题意；

D、=不能判定△ADB∽△ABC，故此选项符合题意．

故选：D．

【点评】本题考查了相似三角形的判定，利用了有两个角对应相等的三角形相似，两边对应成比例且夹角相等的两个三角形相似．

4．【分析】根据相似三角形的判定：两边对应成比例且夹角相等的两三角形相似即可判断．

【解答】解：△ABC中，∠ABC=90°，AB=6，BC=3，AB：BC=2．

A、当点E的坐标为（6，0）时，∠CDE=90°，CD=2，DE=1，则AB：BC=CD：DE，△CDE∽△ABC，故本选项不符合题意；

B、当点E的坐标为（6，3）时，∠CDE=90°，CD=2，DE=2，则AB：BC≠CD：DE，△CDE与△ABC不相似，故本选项符合题意；

C、当点E的坐标为（6，5）时，∠CDE=90°，CD=2，DE=4，则AB：BC=DE：CD，△EDC∽△ABC，故本选项不符合题意；

D、当点E的坐标为（4，2）时，∠ECD=90°，CD=2，CE=1，则AB：BC=CD：CE，△DCE∽△ABC，故本选项不符合题意；

故选：B．

【点评】本题考查了相似三角形的判定，难度中等．牢记判定定理是解题的关键．

5．

【分析】由图可知△ABC与△ACD中∠A为公共角，所以只要再找一组角相等，或一组对应边成比例即可解答．

【解答】解：有三个．

①∠B=∠ACD，再加上∠A为公共角，可以根据有两组角对应相等的两个三角形相似来判定；

②∠ADC=∠ACB，再加上∠A为公共角，可以根据有两组角对应相等的两个三角形相似来判定；

③中∠A不是已知的比例线段的夹角，不正确

④可以根据两组对应边的比相等且相应的夹角相等的两个三角形相似来判定；

故选：C．

【点评】本题考查了相似三角形的判定，此题主要考查学生对相似三角形判定定理的理解和掌握，难度不大，属于基础题，要求学生应熟练掌握．

二．填空题

6. 【分析】两三角形有一公共角，再求夹此公共角的两边对应成比例即可．点E位置未确定，所以应分别讨论，△ABC∽△ADE或△ABC∽△AED．

【解答】解：①当△ADE∽△ABC时，有AD：AE=AB：AC，

∵AB=12，AC=9，AD=4，

∴AE=3；

②当△AED∽△ABC时，有AD：AE=AC：AB，

∵AB=12，AC=9，AD=4，

∴AE=，

故答案为：3或．

【点评】本题考查了学生对相似三角形的判定的掌握情况，注意分类讨论思想的运用．

7．【分析】由两角相等的三角形相似即可得出结论；由两边成比例且夹角相等，得出如果，再由公共角相等得出△ACP与△ABC相似

【解答】解：∵∠A=∠A，∠ACP=∠B，

∴△ACP∽△ABC；

∵，∠A=∠A，

∴△ACP与△ABC；

故答案为：B；．

【点评】本题考查了相似三角形的判定方法；熟练掌握相似三角形的判定方法，注意两边成比例且夹角相等的两个三角形相似．

8. 【分析】根据相似三角形的判定定理：两组对应边的比相等且夹角对应相等的两个三角形相似或有两组角对应相等的两个三角形相似，添加条件可得．

【解答】解：∵∠A=∠D=80°，==，

∴当=，即=，DF=6时，△ABC∽△DEF；

或当∠C=∠F=60°时，△ABC∽△DEF，

故答案为：DF=6．

【点评】本题主要考查相似三角形的判定，解题的关键是熟练掌握相似三角形的判定定理．

9. 【分析】这个点是点Q或G，根据两边成比例夹角相等即可判断．

【解答】解：这个点是点Q．

∵∠ABC=∠QDE，=，=，

∴=，

∴△ABC∽QDE，

同法可得：==，△ABC∽△EDG，

故答案为Q或G．

【点评】本题考查相似三角形的判定和性质，解题的关键是熟练掌握相似三角形的判定方法，属于中考常考题型．

10. 【分析】根据对顶角相等得到∠AEC=∠BED，则根据两组对应边的比相等且夹角对应相等的两个三角形相似，当=时，△BDE∽△ACE，然后利用比例性质计算CE的长．

【解答】解：∵∠AEC=∠BED，

∴当=时，△BDE∽△ACE，

即=，

∴CE=．

故答案为．

【点评】本题考查了相似三角形的判定：两组对应边的比相等且夹角对应相等的两个三角形相似，此判定方法要合理使用公共角或对顶角．

三．解答题

11. 【分析】根据两边成比例夹角相等的两三角形相似即可判断．

【解答】证明：∵BC=4，AC=8，CD=2，∴，
又∵∠C=∠C，
∴△BCD∽△ACB．

【点评】本题考查相似三角形的判定，解题的关键是熟练掌握相似三角形的判定方法，学会利用数形结合的思想思考问题；

12. 【分析】只要证明△AFE∽△BAE，得 ，即可推出，而∠BED=∠BED，可得△FED∽△DEB．

【解答】证明：∵四边形ABCD是矩形，

∴∠BAE=90°，∵∠AFE=∠BFA=90°，

∴∠AFE=∠BAE，∵∠AEF=∠BEA，

∴△AFE∽△BAE，

得 ∴，

又∵AE=ED，

∴

，而∠BED=∠BED，

∴△FED∽△DEB．

【点评】本题考查相似三角形的判定和性质，矩形的性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．