湘教版九年级上册3.4 相似三角形的判定与性质精品当堂达标检测题

3.4.1.4 相似三角形判定定理3

班级：___________姓名：___________得分：__________

（满分：100分，考试时间：40分钟）

一．选择题（共5小题，每题6分）

1．如图，在大小为4×4的正方形网格中各有一个三角形，其中是相似三角形的是（　　）

A．①和② B．②和③ C．①和③ D．②和④ 

2．如图，在三角形纸片ABC中，AB=6，BC=8，AC=4．沿虚线剪下的涂色部分的三角形与△ABC相似的是（　　）

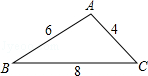
A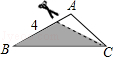． B． 

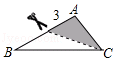C． D．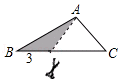 

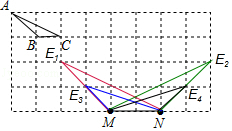
3．各顶点都在格点上的三角形叫格点三角形，如图，在4×8的方格中，以M、N为顶点且与△ABC相似的格点三角形的个数共有（　　）个．

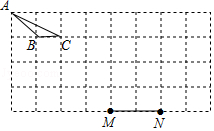
A．3 B．4 C．5 D．6 

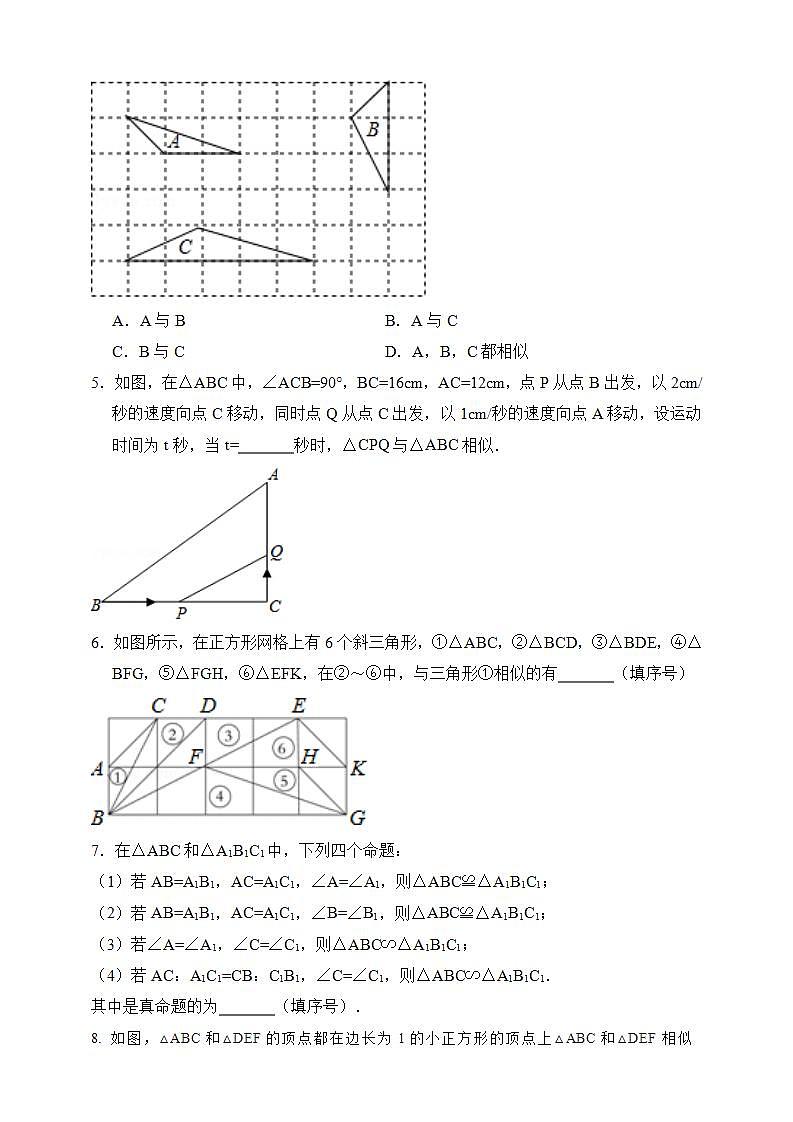
4．下列三个三角形中相似的是（　　）

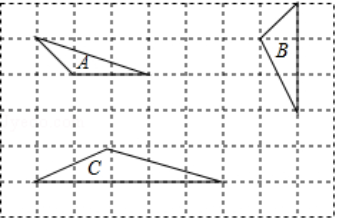
A．A与B  B．A与C 

C．B与C  D．A，B，C都相似 

5．如图，在△ABC中，∠ACB=90°，BC=16cm，AC=12cm，点P从点B出发，以2cm/秒的速度向点C移动，同时点Q从点C出发，以1cm/秒的速度向点A移动，设运动时间为t秒，当t=　   　秒时，△CPQ与△ABC相似．

6．如图所示，在正方形网格上有6个斜三角形，①△ABC，②△BCD，③△BDE，④△BFG，⑤△FGH，⑥△EFK，在②～⑥中，与三角形①相似的有　   　（填序号）

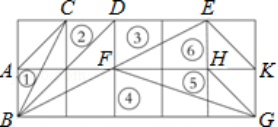
7．在△ABC和△A1B1C1中，下列四个命题：

（1）若AB=A1B1，AC=A1C1，∠A=∠A1，则△ABC≌△A1B1C1；

（2）若AB=A1B1，AC=A1C1，∠B=∠B1，则△ABC≌△A1B1C1；

（3）若∠A=∠A1，∠C=∠C1，则△ABC∽△A1B1C1；

（4）若AC：A1C1=CB：C1B1，∠C=∠C1，则△ABC∽△A1B1C1．

其中是真命题的为　   　（填序号）．

8. 如图，△ABC和△DEF的顶点都在边长为1的小正方形的顶点上△ABC和△DEF相似吗？为什么？

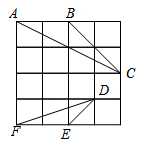
9. 如图，在△ABC和△ADE中，AB/AD=BC/DE=AC/AE，点B．D．E在一条直线上，求证：△ABD∽△ACE．

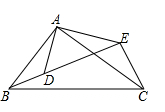
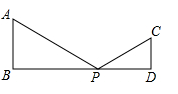
10.如图，AB⊥BD，CD⊥BD，AB=6cm，CD=4cm，BD=14cm，点P在BD上由点B向点D方向移动，当点P移到离点B多远时，△APB和△CPD相似？

试题解析

1．【分析】分别求得四个三角形三边的长，再根据三角形三边分别成比例的两三角形相似来判定．

【解答】解：∵①中的三角形的三边分别是：2，，；

②中的三角形的三边分别是：3，，；

③中的三角形的三边分别是：2，2，2；

④中的三角形的三边分别是：3，，4；

∵①与③中的三角形的三边成比例：==，

∴①与③相似．

故选：C．

【点评】本题考查三组对应边的比相等的两个三角形相似的运用、勾股定理等知识，解题的关键是正确寻找直角三角形，求出三角形的边长，属于中考常考题型．

2．【分析】根据相似三角形的判定分别进行判断即可得出答案即可．

【解答】解：在三角形纸片ABC中，AB=6，BC=8，AC=4．

A、∵==，对应边 ==，≠，

故沿虚线剪下的涂色部分的三角形与△ABC不相似，故此选项错误；

B、∵=，对应边 =，即：=，∠C=∠C，

故沿虚线剪下的涂色部分的三角形与△ABC相似，故此选项正确；

C、∵=，对应边 ==，≠，

故沿虚线剪下的涂色部分的三角形与△ABC不相似，故此选项错误；

D、∵==，

=，≠，

故沿虚线剪下的涂色部分的三角形与△ABC不相似，故此选项错误；

故选：B．

【点评】此题主要考查了相似三角形的判定，正确利用相似三角形两边比值相等切夹角相等的两三角形相似是解题关键．

3．【分析】根据相似三角形的判定定理（三边法：三组对应边的比相等的两个三角形相似）进行解答．

【解答】解：如图，

符合条件的三角形共有4个．

故选：B．

【点评】本题考查了相似三角形的判定．解题时，注意分类讨论数学思想的应用，以防漏解而导致解题错误．

4．【分析】先根据勾股定理的逆定理求出三个三角形各边的长，进而可得出结论．

【解答】解：A中三角形的三边长分别为：2，，；

B中三角形的三边长分别为：3，，；

C中三角形的三边长分别为：5，，．

∵==，

∴A与C相似．

故选：B．

【点评】本题考查的是相似三角形的判定，熟知三条边对应成比例的三角形相似是解答此题的关键．

5．【分析】分CP和CB是对应边，CP和CA是对应边两种情况，利用相似三角形对应边成比例列式计算即可得解．

【解答】解：CP和CB是对应边时，△CPQ∽△CBA，

所以，，

即，

解得t=4.8；

CP和CA是对应边时，△CPQ∽△CAB，

所以，，

即，

解得t=．

综上所述，当t=4.8或时，△CPQ与△CBA相似．

故答案为4.8或．

【点评】本题考查了相似三角形的判定，主要利用了相似三角形对应边成比例，难点在于分情况讨论．

6．【分析】两三角形三条边对应成比例，两三角形相似，据此即可解答．

【解答】解：设每个小正方形的边长为1，则△ABC的各边长分别为1、、．则

②△BCD的各边长分别为1、、2；

③△BDE的各边长分别为2、2、2（为△ABC各边长的2倍）；

④△BFG的各边长分别为5、、（为△ABC各边长的倍）；

⑤△FGH的各边长分别为2、、（为△ABC各边长的倍）；

⑥△EFK的各边长分别为3、、．

根据三组对应边的比相等的两个三角形相似得到与三角形①相似的是③④⑤．

故答案为③④⑤．

【点评】此题考查了相似三角形的判定，勾股定理，掌握三组对应边的比相等的两个三角形相似是解题的关键．

7．【分析】根据全等三角形的判定方法以及相似三角形的判定方法逐项分析即可．

【解答】解：（1）若AB=A1B1，AC=A1C1，∠A=∠A1，则△ABC≌△A1B1C1是正确的，利用SAS判定即可；

（2）若AB=A1B1，AC=A1C1，∠B=∠B1，则△ABC≌△A1B1C1是错误的，SSA不能判定两个三角形全等，角必须是夹角；

（3）若∠A=∠A1，∠C=∠C1，则△ABC∽△A1B1C1是正确的，根据两对角相等的三角形相似判定即可；

（4）若AC：A1C1=CB：C1B1，∠C=∠C1，则△ABC∽△A1B1C1是正确的，根据两边及其夹角法：两组对应边的比相等且夹角对应相等的两个三角形相似判定即可，

综上可知①③④，

故答案为：①③④．

【点评】本题考查了全等三角形的判定以及相似三角形的判定，解题的关键是熟练掌握其各种判定方法并且灵活运用其各种判定方法．

8. 【分析】利用格点三角形的知识求出AB，BC及EF，DE的长度，继而可作出判断．

【解答】解：△ABC和△DEF相似．理由如下：

由勾股定理，得AB=2，AC=2，BC=2，DE=，DF=，EF=2，

∵=，==，==，

∴==，

∴△ABC∽△DEF．

【点评】此题主要考查学生对勾股定理和相似三角形的判定的理解和掌握，解答此题的关键是认真观察图形，得出两个三角形角和角，边和边的关系．

9. 【分析】由在△ABC和△ADE中，，可证得△ABC∽△ADE，即可证得∠BAD=∠CAE，又由，即可证得：△ABD∽△ACE．

【点评】此题考查了相似三角形的判定与性质．此题难度适中，注意掌握数形结合思想的应用．

10. 【分析】设出BP=xcm，由BD﹣BP=PD表示出PD的长，若△ABP∽△PDC，根据相似三角形的对应边成比例可得比例式，把各边的长代入即可列出关于x的方程，求出方程的解即可得到x的值，即为PB的长．

【解答】解：由AB=6cm，CD=4cm，BD=14cm，

设BP=xcm，则PD=（14﹣x）cm，

若△ABP∽△PDC，

则 =，

=，

变形得：14x﹣x2=24，即x2﹣14x+24=0，

因式分解得：（x﹣2）（x﹣12）=0，

解得：x1=2，x2=12，

所以BP=2cm或12cm时，△ABP∽△PDC；

若△ABP∽△CDP，

则 =，

即 =，解得：x=8.4，

∴BP=8.4cm，

综上，BP=2cm或12cm或8.4cm时，△ABP∽△PDC．

【点评】本题考查了相似三角形的判定的应用，注意有两种情况，用的知识点是：当两边对应成比例，且夹角相等的两三角形相似．