初中湘教版3.4 相似三角形的判定与性质优秀同步练习题

这是一份初中湘教版3.4 相似三角形的判定与性质优秀同步练习题，共8页。
3.4.2.1 相似三角形的性质1班级：___________姓名：___________得分：__________（满分：100分，考试时间：40分钟）一．选择题（共5小题，每题6分）1．若△ABC∽△DEF，相似比为2：3，则这两个三角形对应角平分线的比为是（　　）A．2：3 B．3：2 C．4：9 D．9：4 2．若两个相似三角形对应边上的高线之比为3：1，则对应角的平分线之比为（　　）A．9：1 B．6：1 C．3：1 D．：1 3．要制作两个形状相同的三角形框架，其中一个三角形的三边长分别为5cm，6cm和9cm，另一个三角形的最短边长为2.5cm，则它的最长边为（　　）A．3cm B．4cm C．4.5cm D．5cm 4．如图，已知△ADE∽△ACB，若AB=10，AC=8，AD=4，则AE的长是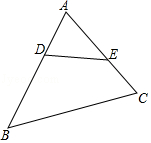（　　）A．4 B．5 C．20 D．3.2 5．如图，△ABC∽△AB'C'，∠A=35°，∠B=72°，则∠AC'B'的度数为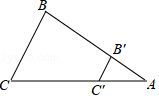（　　）A．63° B．72° C．73° D．83° 二．填空题（共5小题，每题6分）6．若△ABC～△DEF，相似比为3：2，则对应高的比为　   　．7．已知△ABC∽△DEF，其中顶点A、B、C分别对应顶点D、E、F，如果∠A=40°，∠E=60°，那么∠C=　   　度．8．已知△ABC∽△DEF，若△ABC与△DEF的相似比为，则△ABC与△DEF对应中线的比为　   　．9．如图，两个三角形相似，AD=2，AE=3，EC=1，则BD=　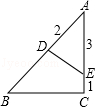   　．10．如图，点A、B、C、D的坐标分别是（1，7）、（1，1）、（4，1）、（6，1），且△CDE∽△ABC，则点E的坐标是　 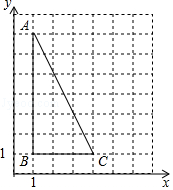  　．三．解答题（共3小题，每题20分）11．如图，点C、D在线段AB上，△PCD是等边三角形，且△ACP∽△PDB．（1）求∠APB的大小．（2）说明线段AC、CD、BD之间的数量关系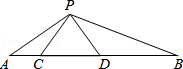．   12．如图，在Rt△ABC中，∠ACB=90°，AC=5cm，∠BAC=60°，动点M从点B出发，在BA边上以每秒2cm的速度向点A匀速运动，同时动点N从点C出发，在CB边上以每秒cm的速度向点B匀速运动，设运动时间为t秒（0≤t≤5），连接MN．（1）若BM=BN，求t的值；（2）若△MBN与△ABC相似，求t的值．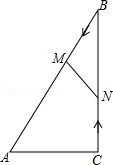 
试题解析一．选择题1．【分析】根据相似三角形对应角平分线的比等于相似比的性质解答．【解答】解：∵两个三角形的相似比为2：3，∴这两个三角形对应角平分线的比为2：3．故选：A．【点评】本题考查了相似三角形的性质：相似三角形对应角平分线的比等于相似比，比较简单．　2．【分析】由相似三角形对应线段的比等于相似比可求得答案．【解答】解：∵两个相似三角形对应高之比是3：1，∴两个相似三角形的相似比是3：1，∴它们的对应角平分线之比为3：1，故选：C．【点评】本题主要考查相似三角形的性质，掌握相似三角形对应线段的比等于相似比是解题的关键．　3．【分析】根据相似三角形的对应边成比例求解可得．【解答】解：设另一个三角形的最长边长为xcm，根据题意，得：=，解得：x=4.5，即另一个三角形的最长边长为4.5cm，故选：C．【点评】本题主要考查相似三角形的性质，解题的关键是掌握相似三角形的对应角相等，对应边的比相等．　4．【分析】直接利用相似三角形的性质得出对应边的比值相等，进而得出答案．【解答】解：∵△ADE∽△ACB，∴=，∵AB=10，AC=8，AD=4，∴=，解得：AE=5．故选：B．【点评】此题主要考查了相似三角形的性质，正确得出比例式是解题关键．　5．【分析】根据三角形内角和定理求出∠C，再根据相似三角形的对应角相等即可解决问题；【解答】解：∵∠A+∠B+∠C=180°，∠A=35°，∠B=72°，∴∠C=180°﹣35°﹣72°=73°，∵△ABC∽△AB'C'，∴∠AC′B′=∠C=73°，故选：C．【点评】本题考查三角形内角和定理、相似三角形的性质等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．二．填空题6．【分析】直接利用相似三角形对应高的比等于相似比进而得出答案．【解答】解：∵△ABC∽△DEF，相似比为3：2，∴对应高的比为：3：2．故答案为：3：2【点评】此题主要考查了相似三角形的性质，正确记忆相关性质是解题关键．　7．【分析】利用相似三角形的性质求出∠B的度数，再根据三角形内角和定理即可解决问题；【解答】解：∵△ABC∽△DEF，∴∠B=∠E=60°，∴∠C=180°﹣∠A﹣∠B=180°﹣40°﹣60°=80°故答案为80；【点评】本题考查相似三角形的性质、内角和定理等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．　8．【分析】根据相似三角形的性质即可求出答案．【解答】解：由于相似三角形的相似比等于对应中线的比，∴△ABC与△DEF对应中线的比为3：4故答案为：3：4【点评】本题考查相似三角形的性质，解题的关键是熟练运用相似三角形的性质，本题属于基础题型．　9．【分析】根据相似三角形的对应边的比相等列出比例式，计算即可．【解答】解：∵△ADE∽△ACB，∴=，即=，解得，BD=4，故答案为：4．【点评】本题考查的是相似三角形的性质，掌握相似三角形的对应边的比相等是解题的关键．10．【分析】根据相似三角形的判定：两边对应成比例且夹角相等的两三角形相似即可判断．【解答】解：△ABC中，∠ABC=90°，AB=6，BC=3，AB：BC=2．①当点E的坐标为（4，0）时，∠CDE=90°，CD=2，DE=1，则AB：BC=CD：DE，△CDE∽△ABC，故正确；②当点E的坐标为（6，5）时，∠CDE=90°，CD=2，DE=4，则AB：BC=DE：CD，△EDC∽△ABC，故正确；③当点E的坐标为（6，2）时，∠ECD=90°，CD=2，CE=1，则AB：BC=CD：CE，△DCE∽△ABC，故正确；同理，当点E的坐标为（4，2）、（4，5）、（6，0），故答案为：（4，0），（6，5），（6，2），（4，2）、（4，5）、（6，0），【点评】本题考查了相似三角形的判定，难度中等．牢记判定定理是解题的关键．三．解答题11．【分析】（1）根据等边三角形的性质得到∠PCD=60°，根据相似三角形的性质得到∠APC=∠PBD，根据三角形内角和定理计算；（2）根据相似三角形的性质、等边三角形的性质解答．【点评】本题考查的是相似三角形的性质、等边三角形的性质，掌握相似三角形的对应边的比相等是解题的关键．12．【分析】（1）由已知条件得出AB=10，BC=5．由题意知：BM=2t，CN=t，BN=5﹣t，由BM=BN得出方程2t=5﹣t，解方程即可；（2）分两种情况：①当△MBN∽△ABC时，由相似三角形的对应边成比例得出比例式，即可得出t的值；②当△NBM∽△ABC时，由相似三角形的对应边成比例得出比例式，即可得出t的值；【解答】解：（1）∵在Rt△ABC中，∠ACB=90°，AC=5，∠BAC=60°，∴∠B=30°，∴AB=2AC=10，BC=5．由题意知：BM=2t，CN=t，∴BN=5﹣t，∵BM=BN，∴2t=5﹣t，解得：t==10﹣15．（2）分两种情况：①当△MBN∽△ABC时，则=，即 =，解得：t=．②当△NBM∽△ABC时，则=，即=，解得：t=．综上所述：当t=或t=时，△MBN与△ABC相似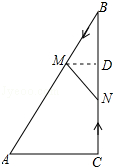．【点评】本题是相似形综合题目，考查了相似三角形的判定与性质、含30°角的直角三角形的性质、三角形面积的计算；本题综合性强，证明三角形相似是解决问题的关键．