初中数学湘教版九年级上册4.3 解直角三角形优秀复习练习题

4.4.1解直角三角形的应用1

班级：___________姓名：___________得分：__________

（每题10分，满分：100分，考试时间：40分钟）

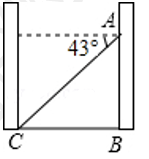
1．如图，小亮站在自家阳台上A处观测到对面大楼底部C的俯角为43°，若两栋楼之间的距离BC为30米，则A处到地面B处的距离AB为多少米？（结果精确到0.1米）（供选用数据：sin43°≈0.6820，cos43°≈0.7314，tan43°≈0.9325）

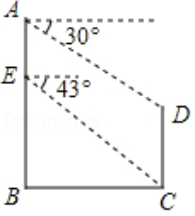
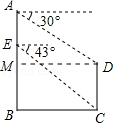
2．如图：两座建筑物AB、CD相距60米，从点A测得D点的俯角为30°，从A点下降10米到E点，在E点测得C点的俯角为43°求两座建筑物的高度．（精确到0.1）（参考数据：≈1.73，cos43°≈0.73，sin43°≈0.68，tan43°≈0.93）

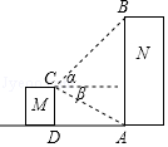
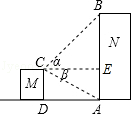
3．如图，在建筑物M的顶端A处测得大楼N顶端B点的仰角α=45°，同时测得大楼底端A点的俯角为β=30°．已知建筑物M的高CD=20米，求楼高AB为多少米？（≈1.732，结果精确到0.1米）

4．我市侯镇二中校园内有一荷花池，荷花池北侧有一水塔．九年级数学兴趣小组

欲利用所学知识测量水塔高度．测量过程如下：先在荷花池南侧A点由测角仪AE测得塔顶仰角为30°，再在荷花池北侧B点由测角仪BF测得塔顶仰角为45°，荷花池AB长为15米，测角仪高均为1.5米，已知A、B、C三点在一条直线上，请根据以上条件求塔高CD？（保留两位小数）

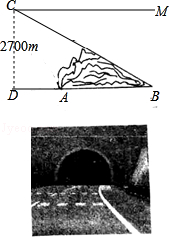
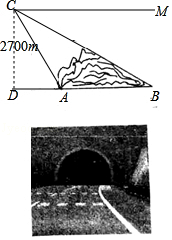
5．乌鞘岭隧道群是连霍国道主干线上隧道最密集、路线最长、海拔最高、地质条件最复杂、施工难度最大的咽喉工程．乌鞘岭特长公路隧道群的全部贯通，将使连霍国道主干线在甘肃境内1608公里路段全部实现高速化，同时也使甘肃河西五市与省会兰州及东南沿海省、市实现全线高速连接．如图，在建设中为确定某隧道AB的长度，测量人员在离地面2700米高度C处的飞机上，测得正前方A、B两点处的俯角分别是60°和30°，求隧道AB的长（结果保留根号）

6．如图，为了测量某山AB的高度，小明先在山脚下C点测得山顶A的仰角为45°，然后沿坡角为30°的斜坡走100到达D点，在D点测得山顶A的仰角为30°，求山AB的高度（精确到0.1米）．（参考数据：≈1.73）

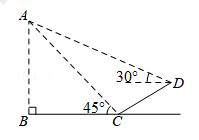
7．某公园的人工湖边上有一座假山，假山顶上有一竖起的建筑物CD，高为10米，数学小组为了测量假山的高度DE，在公园找了一水平地面，在A处测得建筑物点D（即山顶）的仰角为35°，沿水平方向前进20米到达B点，测得建筑物顶部C点的仰角为45°，求假山的高度DE．（结果精确到1米，参考数据：sin35°≈，cos35°≈，tan35°≈）

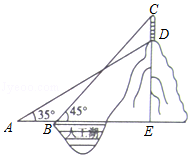
8．我国“蛟龙号”深潜器目前最大的下潜深度达7062米，某天“蛟龙号”在海平面下方2000米的A处作业（如图），测得海底沉船C的俯角∠MAC为45°，其在同一深度向前直线航行2200米到达B点，测得海底沉船C的俯角∠MBC为64.5°（A、BC、M在同一竖直平面内）．请通过计算判断沉船C是否在“蛟龙号”的深潜范围内．（参考数据：sin64.5°≈0.90，cos64.5°≈0.43，tan64.5°≈2.1）

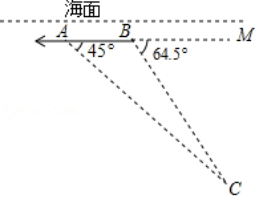
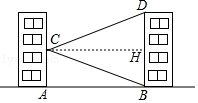
9．如图，学校的实验楼对面是一幢教工宿舍楼，小敏在实验楼的窗口C测得教工宿台楼顶部D仰角为15°，教学楼底部B的俯角为22°，量得实验楼与教学楼之间的距离AB=30m．

（1）求∠BCD的度数．

（2）求教工宿舍楼的高BD．（结果精确到0.1m，参考数据：tanl5°≈0.268，tan22°=0.404）

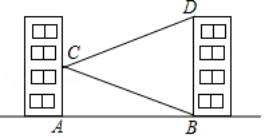
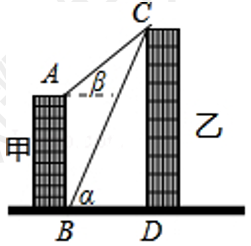
10．如图，线段AB、CD分别表示在同一水平线上的甲、乙两建筑物的高，AB⊥BD，CD⊥BD，垂足分别为B、D．从B点测到C点的仰角α为60°，从A点测得C点的仰角β为30°，甲建筑物的高AB=30米．

（1）求甲、乙两建筑物之间的距离BD．

（2）求乙建筑物的高CD．

试题解析

1．【分析】根据题意和锐角三角函数可以求得AB的长，注意精确到0.1米．

【解答】解：由已知可得，∠ACB=43°，

∵∠ABC=90°，BC=30米，

∴tan∠ACB=，

∴AB=tan43°×30≈0.9325×30≈28.0（米），

答：A处到地面B处的距离AB为28.0米．

【点评】本题考查解直角三角形的应用﹣仰角俯角问题，解答本题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答．

2．【分析】过点D作DM⊥AB于M则DM=BC=6；在Rt△BCE中求出BE，在Rt△ADM中求出AM，即可解决问题；

【解答】解：过点D作DM⊥AB于M则DM=BC=6；

则四边形BCDM是矩形，

∴DM=BC=6，CD=BM，

在Rt△BEC中 tam43°=，

∴BE=BE•tan 43°≈60×0.93=55.8米，

∴AB=AE+BE=10+55.8=65.8米，

在Rt△AMD中 tan30°=，

∴AM=DM•tan 30°=60×，

=20≈34.6米

∴CD=AB﹣AM=65.8﹣34.6=31.2米，

答：AB高为65.8米，CD高为31.2米．

【点评】本题考查解直角三角形的应用，首先构造直角三角形，再借助角边关系、三角函数的定义解题，难度一般．

3．【分析】过点C作CE⊥AB于E，解直角三角形求出CE和CE的长，进而求出AB的长．

【解答】解：如图，过点C作CE⊥AB于E，则AE=CD=20，

∵CE====20，

BE=CEtanα=20×tan45°=20×1=20，

∴AB=AE+EB=20+20≈20×2.732≈54.6（米），

答：楼高AB为54.6米．

【点评】此题主要考查了仰角与俯角的应用，根据已知构造直角三角形利用锐角三角函数关系得出是解题关键．

4．【分析】首先证明FG=DG，在Rt△DEG中，求出x即可解决问题．

【解答】解：根据题意得：BF=AE=GC=1.5m，EF=AB=15m，

设DG=x，

在Rt△DFG中，∠DFG=45°，

∴FG=DG═x（m），

在Rt△DEG中，EG=x（m），

∵EG﹣FG=15

∴x﹣x=15，

解得：x=≈20.25（m），

∴CE=CF+EF=20.25+1.5=21.75（m），

答：塔高约为21.75m．

【点评】本题考查的是解直角三角形的应用﹣仰角俯角问题，掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键．

5．【分析】根据俯角的定义以及平行线的性质可得∠CAD=60°，∠CBD=30°，解直角三角形可得AD，BD的长，相减即可得到AB的长．

【解答】解：由题意得∠ACM=60°，∠BCM=30°．

∵CM∥BD，

∴∠CAD=∠ACM=60°，∠CBD=∠BCM=30°，

∵AD=2700×tan30°=2700×=900m，BD=2700×tan60°=2700m，

∴AB=BD﹣AD=2700﹣900=1800（m）．

答：隧道AB的长为1800m．

【点评】本题考查解直角三角形的应用；利用三角函数值得到与所求线段相关线段的长度是解决本题的关键．

6．【分析】易证△ABC是等腰直角三角形，直角△CDE中已知边CD和∠DCE=30°，则三角形的三边的长度可以得到CE，DE的长度，设BC=x，则AF和DF即可用含x的代数式表示出来，在直角△AFD中，利用三角函数即可得到一个关于x的方程，即可求得x的值．

【解答】解：过D作DE⊥BC于E，作DF⊥AB于F，设AB=x，

在Rt△DEC中，∠DCE=30°，CD=100，

∴DE=50，CE=50，

在Rt△ABC中，∠ACB=45°，

∴BC=x

则AF=AB﹣BF=AB﹣DE=x﹣50

DF=BE=BC+CE=x+50，

在Rt△AFD中，∠ADF=30°，tan30°=，

∴，

∴x=50（3+）≈236.5，

经检验：x=50（3+）是原分式方程的解．

答：山AB的高度约为236.5米

【点评】本题考查仰角的定义，要求学生能借助仰角构造直角三角形，并结合图形利用三角函数解直角三角形．

7．【分析】过点D作水平线的垂线，利用直角三角形中的三角函数解答即可．

【解答】解：过点D作水平线的垂线，即（DE⊥AB），垂足为E，则C、D、E在一条直线上，

设DE的长为x米，

在Rt△BCE中，∠CBE=45°，

∴CE=BE=CD+DE=（10+x）米，

在Rt△ADE中，∠A=35°，

AE=AB+BE=20+10+x=30+x，

tanA=，

∴tan35°=≈，

解得：x≈70，

答：假山的高度DE约为70米．

【点评】此题是解直角三角形的应用﹣﹣﹣仰角和俯角，解本题的关键是利用三角函数解答．

8．【分析】作CD⊥AB于点D，在直角△ACD和直角△BCD中分别利用三角函数表示出AD和BD的长，然后根据AB=AD﹣BD即可列方程求解．

【解答】解：如图，作CD⊥AM于D．

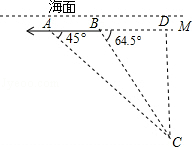
∵CD=AD•tan45°=BD•tan64.5°，

∴AB=AD﹣BD=﹣，

∴CD=AB•==4200（米）．

∴点C深度为4200+2000=6200米＜7062米，

∴沉船C在“蛟龙号”的深潜范围内．

【点评】本题考查俯角的定义，要求学生能借助仰角构造直角三角形并解直角三角形．

9．【分析】（1）作CH⊥BD于H，如图，利用仰角和俯角定义得到∠DCH=15°，∠BCH=22°，然后计算它们的和即可得到∠BCD的度数；

（2）利用正切定义，在Rt△DCH中计算出DH=30tan15°=8.04，在Rt△BCH中计算出BH=30tan22°=12.12，然后计算BH+DH即可得到教工宿舍楼的高BD．

【解答】解：（1）作CH⊥BD于H，如图，

根据题意得∠DCH=15°，∠BCH=22°，

∴∠BCD=∠DCH+∠BCH=15°+22°=37°；

答：教工宿舍楼的高BD为20.1m．

【点评】本题考查了解直角三角形的应用﹣仰角俯角问题：解决此类问题要了解角之间的关系，找到与已知和未知相关联的直角三角形，当图形中没有直角三角形时，要通过作高或垂线构造直角三角形，另当问题以一个实际问题的形式给出时，要善于读懂题意，把实际问题划归为直角三角形中边角关系问题加以解决．

10．【分析】（1）在Rt△CBD中利用三角函数即可求解；

（2）作AE⊥CD于点E，在Rt△ACE中利用三角函数求得CE的长，然后根据CD=CE+DE求解．

【解答】解：（1）作AE⊥CD于点E，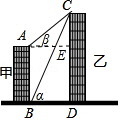

设CE=x，

在Rt△ACE中，∠CAE=30°，则AE=x，可得BD=AE=x；

在Rt△BCD中，∠CBD=60°，则CD=BD=3x，

∵CD=CE+DE，

∴3x=30+x，

解得：x=15，

∴BD=15（米），

答：甲、乙两建筑物之间的距离BD为15米；

（2）由（1）知，CD=3x=45（米），

答：乙建筑物的高CD为45米．

【点评】本题考查了直角三角形中三角函数的应用，考查了特殊角的三角函数值，本题中求的AE的长是解题的关键．