


2022-2023学年临汾市重点中学七下数学期末考试模拟试题含答案
展开
这是一份2022-2023学年临汾市重点中学七下数学期末考试模拟试题含答案,共7页。
2022-2023学年临汾市重点中学七下数学期末考试模拟试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 考生请注意:1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。 一、选择题(每小题3分,共30分)1.张老师和李老师住在同一个小区,离学校3000米,某天早晨,张老师和李老师分别于7点5分、7点15分离家骑自行车上班,刚好在校门口相遇,已知李老师骑车的速度是张老师的1.2倍,为了求他们各自骑自行车的速度,设张老师骑自行车的速度是![]() 米/分,则可列得方程为( )A.
米/分,则可列得方程为( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 2.若
2.若![]() 是完全平方式,则符合条件的k的值是( )A.±3 B.±9 C.-9 D.93.如图,把长方形纸片
是完全平方式,则符合条件的k的值是( )A.±3 B.±9 C.-9 D.93.如图,把长方形纸片![]() 纸沿对角线折叠,设重叠部分为△
纸沿对角线折叠,设重叠部分为△![]() ,那么,下列说法错误的是( )
,那么,下列说法错误的是( )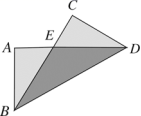 A.△
A.△![]() 是等腰三角形,
是等腰三角形,![]() B.折叠后∠ABE和∠CBD一定相等C.折叠后得到的图形是轴对称图形D.△EBA和△EDC一定是全等三角形4.对于反比例函数
B.折叠后∠ABE和∠CBD一定相等C.折叠后得到的图形是轴对称图形D.△EBA和△EDC一定是全等三角形4.对于反比例函数![]() ,下列说法不正确的是( )A.点
,下列说法不正确的是( )A.点![]() 在它的图像上 B.当
在它的图像上 B.当![]() 时,
时,![]() 随
随![]() 的增大而增大C.它的图像在第二、四象限 D.当
的增大而增大C.它的图像在第二、四象限 D.当![]() 时,
时,![]() 随
随![]() 的增大而减小5.式子
的增大而减小5.式子![]() 在实数范围内有意义,则
在实数范围内有意义,则![]() 的取值范围是( )A.
的取值范围是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 6. “龟兔赛跑”是同学们熟悉的寓言故事.如图所示,表示了寓言中的龟、兔的路程S和时间t的关系(其中直线段表示乌龟,折线段表示兔子).下列叙述正确的是( )
6. “龟兔赛跑”是同学们熟悉的寓言故事.如图所示,表示了寓言中的龟、兔的路程S和时间t的关系(其中直线段表示乌龟,折线段表示兔子).下列叙述正确的是( )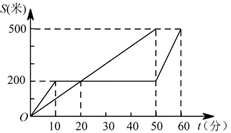 A.赛跑中,兔子共休息了50分钟B.乌龟在这次比赛中的平均速度是0.1米/分钟C.兔子比乌龟早到达终点10分钟D.乌龟追上兔子用了20分钟7.如图,正方形ABCD中,AE垂直于BE,且AE=3,BE=4,则阴影部分的面积是( )
A.赛跑中,兔子共休息了50分钟B.乌龟在这次比赛中的平均速度是0.1米/分钟C.兔子比乌龟早到达终点10分钟D.乌龟追上兔子用了20分钟7.如图,正方形ABCD中,AE垂直于BE,且AE=3,BE=4,则阴影部分的面积是( )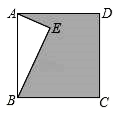 A.16 B.18 C.19 D.218.用配方法解一元二次方程
A.16 B.18 C.19 D.218.用配方法解一元二次方程![]() ,配方后得到的方程是( )A.
,配方后得到的方程是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 9.龙华区某校改造过程中,需要整修校门口一段全长2400m的道路,为了保证开学前师生进出不受影响,实际工作效率比原计划提高了
9.龙华区某校改造过程中,需要整修校门口一段全长2400m的道路,为了保证开学前师生进出不受影响,实际工作效率比原计划提高了![]() ,结果提前8天完成任务,若设原计划每天整个道路x米,根据题意可得方程( )A.
,结果提前8天完成任务,若设原计划每天整个道路x米,根据题意可得方程( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 10.古希腊著名的毕达哥拉斯学派把1、3、6、10…这样的数称为“三角形数”,而把1、4、9、16…这样的数称为“正方形数”.如图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形”之和,下列等式中,符合这一规律的表达式为( )
10.古希腊著名的毕达哥拉斯学派把1、3、6、10…这样的数称为“三角形数”,而把1、4、9、16…这样的数称为“正方形数”.如图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形”之和,下列等式中,符合这一规律的表达式为( )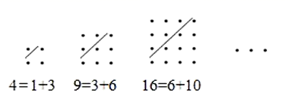 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 二、填空题(本大题共有6小题,每小题3分,共18分)11.八年级两个班一次数学考试的成绩如下:八(1)班46人,平均成绩为86分;八(2)班54人,平均成绩为80分,则这两个班的平均成绩为__分.12.已知
二、填空题(本大题共有6小题,每小题3分,共18分)11.八年级两个班一次数学考试的成绩如下:八(1)班46人,平均成绩为86分;八(2)班54人,平均成绩为80分,则这两个班的平均成绩为__分.12.已知![]() ,
,![]() 是二元一次方程组
是二元一次方程组![]() 的解,则代数式
的解,则代数式![]() 的值为_____.13.若直线l1:y1=k1x+b1经过点(0,3),l2:y2=k2x+b2经过点(3,1),且l1与l2关于x轴对称,则关于x的不等式k1x+b1>k2x+b2的解集为______.14.如图在平面直角坐标系xOy中,直线l经过点A(-1,0),点A1,A2,A3,A4,A5,……按所示的规律排列在直线l上.若直线 l上任意相邻两个点的横坐标都相差1、纵坐标也都相差1,若点An(n为正整数)的横坐标为2015,则n=___________.
的值为_____.13.若直线l1:y1=k1x+b1经过点(0,3),l2:y2=k2x+b2经过点(3,1),且l1与l2关于x轴对称,则关于x的不等式k1x+b1>k2x+b2的解集为______.14.如图在平面直角坐标系xOy中,直线l经过点A(-1,0),点A1,A2,A3,A4,A5,……按所示的规律排列在直线l上.若直线 l上任意相邻两个点的横坐标都相差1、纵坐标也都相差1,若点An(n为正整数)的横坐标为2015,则n=___________.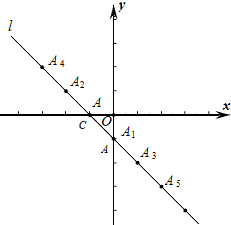 15.已知,如图,矩形ABCD中,E,F分别是AB,AD的中点,若EF=5,则AC=_____.
15.已知,如图,矩形ABCD中,E,F分别是AB,AD的中点,若EF=5,则AC=_____.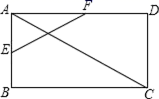 16.如图,一块矩形铁皮的长是宽的2倍,将这个铁皮的四角各剪去一个边长为3cm的小正方形,做成一个无盖的盒子,若盒子的容积是240cm3,则原铁皮的宽为______cm.
16.如图,一块矩形铁皮的长是宽的2倍,将这个铁皮的四角各剪去一个边长为3cm的小正方形,做成一个无盖的盒子,若盒子的容积是240cm3,则原铁皮的宽为______cm. 三、解下列各题(本大题共8小题,共72分)17.(8分)如图:BE、CF是锐角△ABC的两条高,M、N分别是BC、EF的中点,若EF=6,BC=24.
三、解下列各题(本大题共8小题,共72分)17.(8分)如图:BE、CF是锐角△ABC的两条高,M、N分别是BC、EF的中点,若EF=6,BC=24.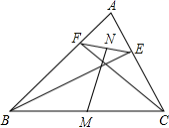 (1)证明:∠ABE=∠ACF; (2)判断EF与MN的位置关系,并证明你的结论;(3)求MN的长. 18.(8分) (1)分解因式:
(1)证明:∠ABE=∠ACF; (2)判断EF与MN的位置关系,并证明你的结论;(3)求MN的长. 18.(8分) (1)分解因式:![]() (2)解方程:
(2)解方程:![]() 19.(8分)有这样一个问题:探究函数
19.(8分)有这样一个问题:探究函数![]() 的图象与性质.小亮根据学习函数的经验,对函数
的图象与性质.小亮根据学习函数的经验,对函数![]() 的图象与性质进行了探究。下面是小亮的探究过程,请补充完整:(1)函数
的图象与性质进行了探究。下面是小亮的探究过程,请补充完整:(1)函数![]() 中自变量x的取值范围是_________.(2)下表是y与x的几组对应值.x…-3-2-10
中自变量x的取值范围是_________.(2)下表是y与x的几组对应值.x…-3-2-10![]()
![]() 2345…y…-
2345…y…-![]() -
-![]() -4-5-7m-1-2-
-4-5-7m-1-2-![]() -
-![]() …求m的值;(3)在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;(4)根据画出的函数图象,发现下列特征:该函数的图象与直线x=1越来越靠近而永不相交,该函数的图象还与直线_________越来越靠近而永不相交.
…求m的值;(3)在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;(4)根据画出的函数图象,发现下列特征:该函数的图象与直线x=1越来越靠近而永不相交,该函数的图象还与直线_________越来越靠近而永不相交.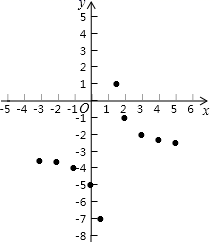 20.(8分)先化简,再求值:
20.(8分)先化简,再求值: ![]() ,其中
,其中![]() . 21.(8分)先化简,再求值:
. 21.(8分)先化简,再求值: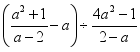 ,其中
,其中![]() 是满足不等式组
是满足不等式组![]() 的整数解. 22.(10分)如图①,在平面直角坐标系中,直线
的整数解. 22.(10分)如图①,在平面直角坐标系中,直线![]() :
:![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() 、
、![]() ,且与直线
,且与直线![]() :
:![]() 交于点
交于点![]() ,以线段
,以线段![]() 为边在直线
为边在直线![]() 的下方作正方形
的下方作正方形![]() ,此时点
,此时点![]() 恰好落在
恰好落在![]() 轴上.
轴上.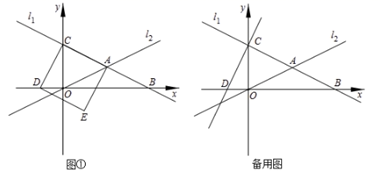 (1)求出
(1)求出![]() 三点的坐标.(2)求直线
三点的坐标.(2)求直线![]() 的函数表达式.(3)在(2)的条件下,点
的函数表达式.(3)在(2)的条件下,点![]() 是射线
是射线![]() 上的一个动点,在平面内是否存在点
上的一个动点,在平面内是否存在点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形?若存在,直接写出点
为顶点的四边形是菱形?若存在,直接写出点![]() 的坐标;若不存在,请说明理由. 23.(10分)如图,已知点A、C在双曲线
的坐标;若不存在,请说明理由. 23.(10分)如图,已知点A、C在双曲线![]() 上,点 B、D在双曲线
上,点 B、D在双曲线![]() 上,AD// BC//y 轴.(I)当m=6,n=-3,AD=3 时,求此时点 A 的坐标;(II)若点A、C关于原点O对称,试判断四边形 ABCD的形状,并说明理由;(III)若AD=3,BC=4,梯形ABCD的面积为
上,AD// BC//y 轴.(I)当m=6,n=-3,AD=3 时,求此时点 A 的坐标;(II)若点A、C关于原点O对称,试判断四边形 ABCD的形状,并说明理由;(III)若AD=3,BC=4,梯形ABCD的面积为![]() ,求mn 的最小值.
,求mn 的最小值.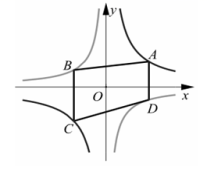 24.(12分)如图,四边形
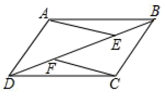
24.(12分)如图,四边形![]() 是平行四边形,
是平行四边形,![]() 、
、![]() 是对角线
是对角线![]() 上的两个点,且
上的两个点,且![]() .求证:
.求证:![]() .
. 参考答案 一、选择题(每小题3分,共30分)1、A2、D3、B4、D5、D6、D7、C8、B9、A10、D 二、填空题(本大题共有6小题,每小题3分,共18分)11、82.112、113、x<
参考答案 一、选择题(每小题3分,共30分)1、A2、D3、B4、D5、D6、D7、C8、B9、A10、D 二、填空题(本大题共有6小题,每小题3分,共18分)11、82.112、113、x<![]() 14、4031.15、1.16、1. 三、解下列各题(本大题共8小题,共72分)17、(1)证明见解析;(2)
14、4031.15、1.16、1. 三、解下列各题(本大题共8小题,共72分)17、(1)证明见解析;(2)![]() 垂直平分
垂直平分![]() .(3)
.(3)![]() .18、(1)
.18、(1)![]() ;(2)无解19、 (1)
;(2)无解19、 (1)![]() ;(2)1;(2)见解析;(4)y=-2.20、
;(2)1;(2)见解析;(4)y=-2.20、![]() ,121、化简得:
,121、化简得:![]() 求值得:
求值得:![]() .22、(1)
.22、(1)![]()
![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() ;(3)存在,
;(3)存在,![]() ,
,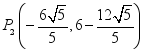 ,
,![]() .23、 (I) 点
.23、 (I) 点![]() 的坐标为
的坐标为![]() ;(II) 四边形
;(II) 四边形![]() 是平行四边形,理由见解析;(III)
是平行四边形,理由见解析;(III) ![]() 的最小值是
的最小值是![]() .24、见解析
.24、见解析
相关试卷
这是一份重庆市重点中学2022-2023学年七下数学期末考试模拟试题含答案,共8页。试卷主要包含了下列事件中是必然事件的是,数据3,2,0,1,的方差等于等内容,欢迎下载使用。
这是一份承德市重点中学2022-2023学年数学七下期末考试模拟试题含答案,共6页。
这是一份2022-2023学年白城市重点中学七下数学期末考试模拟试题含答案,共8页。试卷主要包含了考生必须保证答题卡的整洁,下列事件中,属于随机事件的是,已知等内容,欢迎下载使用。









