2022-2023学年上海市闵行区闵行区莘松中学七下数学期末监测试题含答案

这是一份2022-2023学年上海市闵行区闵行区莘松中学七下数学期末监测试题含答案，共6页。
2022-2023学年上海市闵行区闵行区莘松中学七下数学期末监测试题（时间：120分钟             分数：120分） 学校_______            年级_______        姓名_______ 考生请注意：1．答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内，不得在试卷上作任何标记。2．第一部分选择题每小题选出答案后，需将答案写在试卷指定的括号内，第二部分非选择题答案写在试卷题目指定的位置上。3．考生必须保证答题卡的整洁。考试结束后，请将本试卷和答题卡一并交回。 一、选择题(每小题3分,共30分)1．《九章算术》记载“今有邑方不知大小，各中开门．出北门三十步有木，出西门七百五十步见木．问邑方有几何？”意思是：如图，点M、点N分别是正方形ABCD的边AD、AB的中点，ME⊥AD，NF⊥AB，EF过点A，且ME=30步，NF=750步，则正方形的边长为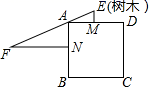（　　）A．150步 B．200步 C．250步 D．300步2．如图,在矩形ABCD中,AB=6,BC=8,若将矩形折叠,使B点与D点重合,则折痕EF的长为( )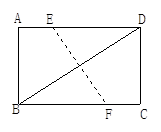A． B． C．5 D．63．已知m2-n2=mn，则的值等于（　　）A．1 B．0 C．-1 D．-4．方程x（x﹣1）＝0的根是（　　）A．x＝0 B．x＝1 C．x1＝0，x2＝1 D．x1＝0，x2＝﹣15．下列选项中，可以用来证明命题“若a²>1,则a＞1”是假命题的反例是（ ）A．a=－2. B．a==－1 C．a=1 D．a=26．运用分式基本性质，等式中缺少的分子为（    ）A．a B．2a C．3a D．4a7． “a是正数”用不等式表示为（　　）A．a≤0    B．a≥0    C．a＜0    D．a＞08．函数y=中自变量x的取值范围为（　　）A．x≥0 B．x≥-1 C．x＞-1 D．x≥19．一组数中，无理数的个数是（    ）A．2 B．3 C．4 D．510．﹣3x＜﹣1的解集是（ ）A．x＜ B．x＜﹣ C．x＞ D．x＞﹣二、填空题(本大题共有6小题，每小题3分，共18分)11．已知：如图，平行四边形中，平分交于，平分交于，若，，则___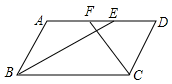．12．甲、乙两家人，相约周末前往中梁国际慢城度周末，甲、乙两家人分别从上桥和童家桥驾车同时出发，匀速前进，且甲途经童家桥，并以相同的线路前往中梁国际慢城. 已知乙的车速为30千米/小时，设两车之间的里程为y（千米），行驶时间为x（小时），图中的折线表示从两家人出发至甲先到达终点的过程中y（千米）与x（小时）的函数关系，根据图中信息，甲的车速为_______千米/小时.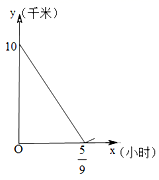13．已知的对角线，相交于点，是等边三角形，且，则的长为__________．14．如果点A(1，n)在一次函数y＝3x﹣2的图象上，那么n＝_____．15．分解因式:__________．16．化简：＝_______．三、解下列各题(本大题共8小题，共72分)17．（8分）某公司欲招聘一名公务人员，对甲、乙两位应试者进行了面试和笔试，他们的成绩（百分制）如表所示：应试者面试笔试甲8690乙9283（1）如果公司认为面试和笔试同等重要，从他们的成绩看，谁将被录取？（2）如果公司认为作为公务人员面试成绩应该比笔试成绩更重要，并分别赋予它们6和4的权，计算甲、乙两人各自的平均成绩，谁将被录取？   18．（8分）当k值相同时，我们把正比例函数与反比例函数叫做“关联函数”.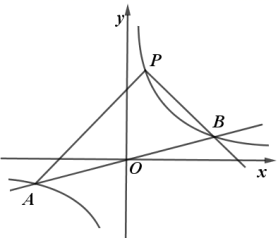(1)如图，若k>0，这两个函数图象的交点分别为A，B，求点A，B的坐标（用k表示）；(2)若k=1，点P是函数在第一象限内的图象上的一个动点（点P不与B重合），设点P的坐标为（），其中m>0且m≠2.作直线PA，PB分别与x轴交于点C，D，则△PCD是等腰三角形，请说明理由；(3)在(2)的基础上，是否存在点P使△PCD为直角三角形？若存在，请求出点P的坐标；若不存在，请说明理由.   19．（8分）如图O为坐标原点，四边形ABCD是菱形，A(4，4)，B点在第二象限，AB＝5，AB与y轴交于点F，对角线AC交y轴于点E(1)直接写出B、C点的坐标；(2)动点P从C点出发以每秒1个单位的速度沿折线段C﹣D﹣A运动，设运动时间为t秒，请用含t的代数式表示△EDP的面积；(3)在(2)的条件下，是否存在一点P，使△APE沿其一边翻折构成的四边形是菱形？若存在，请直接写出当t为多少秒时存在符合条件的点P；若不存在，请说明理由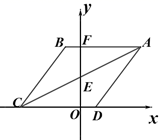．   20．（8分）关于的方程,其中分别是的三边长.(1)若方程有两个相等的实数根，试判断的形状，并说明理由；(2)若为等边三角形，试求出这个方程的解.   21．（8分）在Rt△ABC中，∠B=900，AC=100cm, ∠A=600,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动，同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动，设点D、E运动的时间是t秒（0＜t≤25）过点D作DF⊥BC于点F，连结DE、EF。（1）四边形AEFD能够成为菱形吗？若能，求相应的t值，若不能，请说明理由。（2）当t为何值时，△DEF为直角三角形？请说明理由。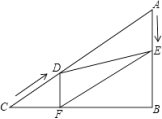   22．（10分）近年来，萧山区大力发展旅游业，跨湖桥遗址、湘湖二期三期、宋城千古情、河上民俗、大美进化……这些名词，相信同学们都耳熟能详了，因此近年来，我区的年游客接待量呈逐年稳步上升，2015年接待1800万人次，2015——2017年这三年累计接待游客高达5958万人次.(1)求萧山区2015——2017年年游客接待量的年平均增长率.(2)若继续呈该趋势增长，请预测2018年年游客接待量（近似到万人次）.   23．（10分）计算：（1）（2）（﹣1）2﹣（﹣）（+）   24．（12分）如图，已知在中，分别是的中点，连结.(1)求证：四边形是平行四边形；(2)若，求四边形的周长.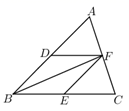   参考答案 一、选择题(每小题3分,共30分)1、D2、A3、C4、C5、A6、D7、D8、B9、B10、C 二、填空题(本大题共有6小题，每小题3分，共18分)11、112、113、．14、115、16、 三、解下列各题(本大题共8小题，共72分)17、 (1)甲将被录取；(2)乙将被录取.18、（1）点A坐标为（-k，-1），点B坐标（k，1）；（2）△PCD是等腰三角形；，理由见解析；（3）不存在，理由见解析．19、 (1)B(-1，4)，C(-4，0)；见解析；(3)或7.5.20、（1）是直角三角形；理由见解析；（2），.21、（1）能，10；（2） 或12,理由见解析.22、（1）年平均增长率为10% ；（2）.23、（1）；（2）24、 (1)见解析； (2)四边形的周长为12.