


2022-2023学年云南省昆明市八校联考数学七下期末质量跟踪监视试题含答案
展开
这是一份2022-2023学年云南省昆明市八校联考数学七下期末质量跟踪监视试题含答案,共8页。
2022-2023学年云南省昆明市八校联考数学七下期末质量跟踪监视试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 注意事项:1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。2.答题时请按要求用笔。3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。5.保持卡面清洁,不要折暴、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。 一、选择题(每小题3分,共30分)1.某单位向一所希望小学赠送1080本课外书,现用A、B两种不同的包装箱进行包装,单独使用B型包装箱比单独使用A型包装箱可少用6个;已知每个B型包装箱比每个A型包装箱可多装15本课外书.若设每个A型包装箱可以装书x本,则根据题意列得方程为( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 2.若关于x的分式方程
2.若关于x的分式方程![]() 的解为x =2,则m的值为( ) .A.2 B.0 C.6 D.43.分式方程
的解为x =2,则m的值为( ) .A.2 B.0 C.6 D.43.分式方程![]() 的解为( )A.x=-2 B.x=-3 C.x=2 D.x=34.根据天气预报,2018年6月20日双流区最高气温是
的解为( )A.x=-2 B.x=-3 C.x=2 D.x=34.根据天气预报,2018年6月20日双流区最高气温是![]() ,最低气温是
,最低气温是![]() ,则双流区气温
,则双流区气温![]() 的变化范围是( )A.
的变化范围是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 5.如图,已知一次函数y=kx+b的图象经过A、B两点,那么不等式kx+b>0的解集是( )
5.如图,已知一次函数y=kx+b的图象经过A、B两点,那么不等式kx+b>0的解集是( )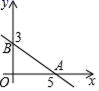 A.x>3 B.x<3 C.x>5 D.x<56.甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟.在整个步行过程中,甲、乙两人的距离
A.x>3 B.x<3 C.x>5 D.x<56.甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟.在整个步行过程中,甲、乙两人的距离![]() (米)与甲出发的时间
(米)与甲出发的时间![]() (分)之间的关系如图所示,下列结论:①甲步行的速度为60米/分;②乙用16分钟追上甲;③乙走完全程用了30分钟;④乙到达终点时甲离终点还有360米.其中正确的结论有( )
(分)之间的关系如图所示,下列结论:①甲步行的速度为60米/分;②乙用16分钟追上甲;③乙走完全程用了30分钟;④乙到达终点时甲离终点还有360米.其中正确的结论有( )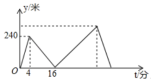 A.1个 B.2个 C.3个 D.4个7.关于x的不等式
A.1个 B.2个 C.3个 D.4个7.关于x的不等式![]() 的解集为x>3,那么a的取值范围为( )A.a>3 B.a<3 C.a≥3 D.a≤38.下列交通标志图案中,是中心对称图形的是( )A.
的解集为x>3,那么a的取值范围为( )A.a>3 B.a<3 C.a≥3 D.a≤38.下列交通标志图案中,是中心对称图形的是( )A. B.
B. C.
C. D.
D. 9.将一张平行四边形的纸片折一次,使得折痕平分这个平行四边形的面积.则这样的折纸方法共有( )A.2种 B.4种 C.6种 D.无数种10.已知一次函数y=kx+b的图象如图,则k、b的符号是( )
9.将一张平行四边形的纸片折一次,使得折痕平分这个平行四边形的面积.则这样的折纸方法共有( )A.2种 B.4种 C.6种 D.无数种10.已知一次函数y=kx+b的图象如图,则k、b的符号是( )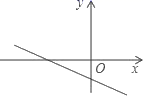 A.k>0,b>0 B.k>0,b<0 C.k<0,b>0 D.k<0,b<0二、填空题(本大题共有6小题,每小题3分,共18分)11.如图,矩形ABCD中,AB=6,BC=8,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,BE的长为_____.
A.k>0,b>0 B.k>0,b<0 C.k<0,b>0 D.k<0,b<0二、填空题(本大题共有6小题,每小题3分,共18分)11.如图,矩形ABCD中,AB=6,BC=8,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,BE的长为_____.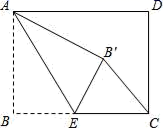 12.如图,正方形ABCD的边长为2,MN∥BC分别交AB、CD于点M、N,在MN上任取两点P、Q,那么图中阴影部分的面积是_____.
12.如图,正方形ABCD的边长为2,MN∥BC分别交AB、CD于点M、N,在MN上任取两点P、Q,那么图中阴影部分的面积是_____.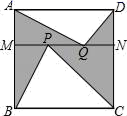 13.如图,反比例函数
13.如图,反比例函数![]() 与正比例函数
与正比例函数![]() 和
和![]() 的图像分别交于点A(2,2)和B(b,3),则关于x的不等式组
的图像分别交于点A(2,2)和B(b,3),则关于x的不等式组 的解集为___________。
的解集为___________。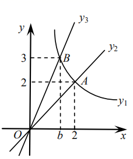 14.某市出租车白天的收费起步价为10元,即路程不超过
14.某市出租车白天的收费起步价为10元,即路程不超过![]() 时收费10元,超过部分每千米收费2元,如果乘客白天乘坐出租车的路程为
时收费10元,超过部分每千米收费2元,如果乘客白天乘坐出租车的路程为![]() ,乘车费为
,乘车费为![]() 元,那么
元,那么![]() 与
与![]() 之间的关系式为__________________.15.将点
之间的关系式为__________________.15.将点![]() 先向左平移6个单位,再向下平移4个单位得到点
先向左平移6个单位,再向下平移4个单位得到点![]() ,则
,则![]() 的坐标是__.16.在参加“森林重庆”的植树活动中,某班六个绿化小组植树的棵数分别是:10,1,1,10,11,1.则这组数据的众数是____________.三、解下列各题(本大题共8小题,共72分)17.(8分)如图,平面直角坐标系中,反比例函数y1=
的坐标是__.16.在参加“森林重庆”的植树活动中,某班六个绿化小组植树的棵数分别是:10,1,1,10,11,1.则这组数据的众数是____________.三、解下列各题(本大题共8小题,共72分)17.(8分)如图,平面直角坐标系中,反比例函数y1=![]() 的图象与函数y2=mx图象交于点A,过点A作AB⊥x轴于点B,已知点A坐标(2,1).(1)求反比例函数解析式;(2)当y2>y1时,求x的取值范围.
的图象与函数y2=mx图象交于点A,过点A作AB⊥x轴于点B,已知点A坐标(2,1).(1)求反比例函数解析式;(2)当y2>y1时,求x的取值范围.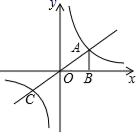 18.(8分)如图,在矩形ABCD中,AB=8,BC=6,点P、点E分别是边AB、BC上的动点,连结DP、PE.将 △ADP 与 △BPE分别沿DP与PE折叠,点A与点B分别落在点A′,B′处.(1) 当点P运动到边AB的中点处时,点A′与点B′重合于点F处,过点C作CK⊥EF于K,求CK的长;(2) 当点P运动到某一时刻,若P,A',B'三点恰好在同一直线上,且A'B'=4 ,试求此时AP的长.
18.(8分)如图,在矩形ABCD中,AB=8,BC=6,点P、点E分别是边AB、BC上的动点,连结DP、PE.将 △ADP 与 △BPE分别沿DP与PE折叠,点A与点B分别落在点A′,B′处.(1) 当点P运动到边AB的中点处时,点A′与点B′重合于点F处,过点C作CK⊥EF于K,求CK的长;(2) 当点P运动到某一时刻,若P,A',B'三点恰好在同一直线上,且A'B'=4 ,试求此时AP的长.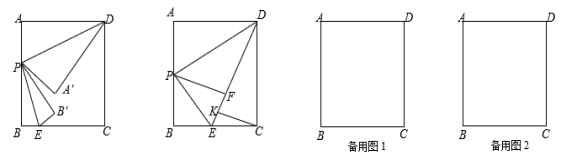 19.(8分)为了落实党的“精准扶贫”政策,A、B两城决定向C、D两乡运送肥料以支持农村生产,已知A、B两城共有肥料500吨,其中A城肥料比B城少100吨,从A城往C、D两乡运肥料的费用分别为20元/吨和25元/吨;从B城往C、D两乡运肥料的费用分别为15元/吨和24元/吨.现C乡需要肥料240吨,D乡需要肥料260吨.(1)A城和B城各有多少吨肥料?(2)设从A城运往C乡肥料x吨,总运费为y元,求出最少总运费.(3)由于更换车型,使A城运往C乡的运费每吨减少a(0<a<6)元,这时怎样调运才能使总运费最少? 20.(8分)某村为绿化村道,计划在村道两旁种植 A、B 两种树木,需要购买这两种树苗 800 棵,A、B 两种树苗的相关信息如表: 树苗 单价(元/棵) 成活率 植树费(元/棵) A 100 80% 20 B 150 90% 20 设购买 A 种树苗 x 棵,绿化村道的总费用为 y 元,解答下列问题: (1)求出 y 与 x 之间的函数关系式.(2)若这批树苗种植后成活了 670 棵,则绿化村道的总费用需要多少元? (3)若绿化村道的总费用不超过 120000 元,则最多可购买 B 种树苗多少棵? 21.(8分)如图,D是△ABC内一点,连接DB、DC、DA,并将AB、DB、DC、AC的中点E、H、G、F依次连接,得到四边形EHGF.
19.(8分)为了落实党的“精准扶贫”政策,A、B两城决定向C、D两乡运送肥料以支持农村生产,已知A、B两城共有肥料500吨,其中A城肥料比B城少100吨,从A城往C、D两乡运肥料的费用分别为20元/吨和25元/吨;从B城往C、D两乡运肥料的费用分别为15元/吨和24元/吨.现C乡需要肥料240吨,D乡需要肥料260吨.(1)A城和B城各有多少吨肥料?(2)设从A城运往C乡肥料x吨,总运费为y元,求出最少总运费.(3)由于更换车型,使A城运往C乡的运费每吨减少a(0<a<6)元,这时怎样调运才能使总运费最少? 20.(8分)某村为绿化村道,计划在村道两旁种植 A、B 两种树木,需要购买这两种树苗 800 棵,A、B 两种树苗的相关信息如表: 树苗 单价(元/棵) 成活率 植树费(元/棵) A 100 80% 20 B 150 90% 20 设购买 A 种树苗 x 棵,绿化村道的总费用为 y 元,解答下列问题: (1)求出 y 与 x 之间的函数关系式.(2)若这批树苗种植后成活了 670 棵,则绿化村道的总费用需要多少元? (3)若绿化村道的总费用不超过 120000 元,则最多可购买 B 种树苗多少棵? 21.(8分)如图,D是△ABC内一点,连接DB、DC、DA,并将AB、DB、DC、AC的中点E、H、G、F依次连接,得到四边形EHGF.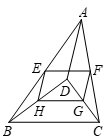 (1)求证:四边形EHGF是平行四边形;(2)若BD⊥CD,AD=7,BD=8,CD=6,求四边形EHGF的周长. 22.(10分)如图①,在平面直角坐标系中,直线
(1)求证:四边形EHGF是平行四边形;(2)若BD⊥CD,AD=7,BD=8,CD=6,求四边形EHGF的周长. 22.(10分)如图①,在平面直角坐标系中,直线![]() :
:![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() 、
、![]() ,且与直线
,且与直线![]() :
:![]() 交于点
交于点![]() ,以线段
,以线段![]() 为边在直线
为边在直线![]() 的下方作正方形
的下方作正方形![]() ,此时点
,此时点![]() 恰好落在
恰好落在![]() 轴上.
轴上.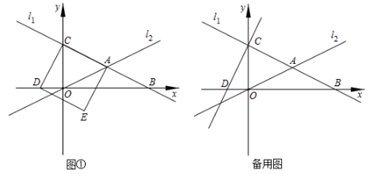 (1)求出
(1)求出![]() 三点的坐标.(2)求直线
三点的坐标.(2)求直线![]() 的函数表达式.(3)在(2)的条件下,点
的函数表达式.(3)在(2)的条件下,点![]() 是射线
是射线![]() 上的一个动点,在平面内是否存在点
上的一个动点,在平面内是否存在点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形?若存在,直接写出点
为顶点的四边形是菱形?若存在,直接写出点![]() 的坐标;若不存在,请说明理由. 23.(10分)如图1,在平面直角坐标系中,点O是坐标原点,四边形ABCO是菱形,点A的坐标为(﹣3,4),点C在x轴的正半轴上,直线AC交y轴于点M,AB边交y轴于点H,连接BM.
的坐标;若不存在,请说明理由. 23.(10分)如图1,在平面直角坐标系中,点O是坐标原点,四边形ABCO是菱形,点A的坐标为(﹣3,4),点C在x轴的正半轴上,直线AC交y轴于点M,AB边交y轴于点H,连接BM.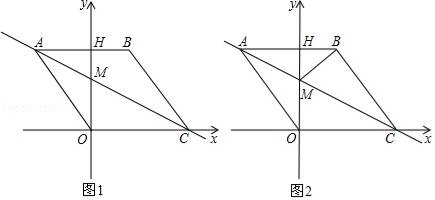 (1)菱形ABCO的边长 (2)求直线AC的解析式;(3)动点P从点A出发,沿折线ABC方向以2个单位/秒的速度向终点C匀速运动,设△PMB的面积为S(S≠0),点P的运动时间为t秒,①当0<t<
(1)菱形ABCO的边长 (2)求直线AC的解析式;(3)动点P从点A出发,沿折线ABC方向以2个单位/秒的速度向终点C匀速运动,设△PMB的面积为S(S≠0),点P的运动时间为t秒,①当0<t<![]() 时,求S与t之间的函数关系式;②在点P运动过程中,当S=3,请直接写出t的值. 24.(12分)如图,正方形网格中每个小正方形的边长都是1个单位长度,每个小正方形的顶点叫做格点,已知△ABC的三个顶点都是格点,请按要求画出三角形.
时,求S与t之间的函数关系式;②在点P运动过程中,当S=3,请直接写出t的值. 24.(12分)如图,正方形网格中每个小正方形的边长都是1个单位长度,每个小正方形的顶点叫做格点,已知△ABC的三个顶点都是格点,请按要求画出三角形.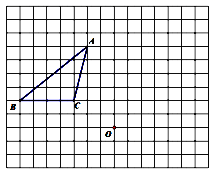 (1)将△ABC先上平移1个单位长度再向右平移2个单位长度,得到△A'B'C';(2)将△A'B'C'绕格点O顺时针旋转90°,得到△A''B''C''. 参考答案 一、选择题(每小题3分,共30分)1、C2、C3、B4、D5、D6、C7、D8、C9、D10、D 二、填空题(本大题共有6小题,每小题3分,共18分)11、3或1.12、113、
(1)将△ABC先上平移1个单位长度再向右平移2个单位长度,得到△A'B'C';(2)将△A'B'C'绕格点O顺时针旋转90°,得到△A''B''C''. 参考答案 一、选择题(每小题3分,共30分)1、C2、C3、B4、D5、D6、C7、D8、C9、D10、D 二、填空题(本大题共有6小题,每小题3分,共18分)11、3或1.12、113、![]() 14、
14、![]() 15、
15、![]() 16、1 三、解下列各题(本大题共8小题,共72分)17、(1)反比例函数的解析式为y=
16、1 三、解下列各题(本大题共8小题,共72分)17、(1)反比例函数的解析式为y=![]() ;(1)﹣1<x<0或x>1. .18、(1)
;(1)﹣1<x<0或x>1. .18、(1)![]() ;(2),PA的长为2或1.19、(1)A城和B城分别有200吨和300吨肥料;(2)从A城运往D乡200吨,从B城运往C乡肥料240吨,运往D乡60吨时,运费最少,最少运费是10040元;(3)当0<a<4时, A城200吨肥料都运往D乡,B城240吨运往C乡,60吨运往D乡;当a=4时,在0≤x≤200范围内的哪种调运方案费用都一样;当4<a<6时, A城200吨肥料都运往C乡,B城40吨运往C乡,260吨运往D乡.20、(1)y=—50x+136000;(2)111000 元.(3)若绿化村道的总费用不超过 120000 元,则最多可购买 B 种树苗 1 棵.21、(1)见解析;(2)122、(1)
;(2),PA的长为2或1.19、(1)A城和B城分别有200吨和300吨肥料;(2)从A城运往D乡200吨,从B城运往C乡肥料240吨,运往D乡60吨时,运费最少,最少运费是10040元;(3)当0<a<4时, A城200吨肥料都运往D乡,B城240吨运往C乡,60吨运往D乡;当a=4时,在0≤x≤200范围内的哪种调运方案费用都一样;当4<a<6时, A城200吨肥料都运往C乡,B城40吨运往C乡,260吨运往D乡.20、(1)y=—50x+136000;(2)111000 元.(3)若绿化村道的总费用不超过 120000 元,则最多可购买 B 种树苗 1 棵.21、(1)见解析;(2)122、(1)![]()
![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() ;(3)存在,
;(3)存在,![]() ,
,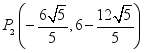 ,
,![]() .23、(1)5;(2)直线AC的解析式y=﹣
.23、(1)5;(2)直线AC的解析式y=﹣![]() x+
x+![]() ;(3)见解析.24、(1)见解析;(2)见解析.
;(3)见解析.24、(1)见解析;(2)见解析.
相关试卷
这是一份山东省青岛李沧区四校联考2022-2023学年七下数学期末质量跟踪监视模拟试题含答案,共6页。试卷主要包含了化简的结果是,兴趣小组的同学要测量树的高度等内容,欢迎下载使用。
这是一份2022-2023学年辽宁省大连高新园区四校联考七下数学期末质量跟踪监视试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁等内容,欢迎下载使用。
这是一份2022-2023学年福建省泉州洛江区七校联考数学七下期末质量跟踪监视模拟试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,函数中,自变量x的取值范围是,分式方程的解为等内容,欢迎下载使用。










