

2022-2023学年云南省曲靖市罗平县数学七年级第二学期期末监测试题含答案
展开
这是一份2022-2023学年云南省曲靖市罗平县数学七年级第二学期期末监测试题含答案,共6页。
2022-2023学年云南省曲靖市罗平县数学七年级第二学期期末监测试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 注意事项:1. 答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。2.选择题必须使用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。4.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.抛物线y=x2﹣4x+5的顶点坐标是( )A.(2,1) B.(﹣2,1) C.(2,5) D.(﹣2,5)2.化简![]() 的结果是( )A.
的结果是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 3.下列说法中,正确的是( )A.一组对边平行,另一组对边相等的四边形是平行四边形 B.对角线相等的四边形是矩形C.有一组邻边相等的矩形是正方形 D.对角线互相垂直的四边形是菱形4.矩形、菱形、正方形都具有的性质是( )A.对角线相等 B.对角线互相平分 C.对角线互相垂直 D.对角线互相平分且相等5.若一次函数
3.下列说法中,正确的是( )A.一组对边平行,另一组对边相等的四边形是平行四边形 B.对角线相等的四边形是矩形C.有一组邻边相等的矩形是正方形 D.对角线互相垂直的四边形是菱形4.矩形、菱形、正方形都具有的性质是( )A.对角线相等 B.对角线互相平分 C.对角线互相垂直 D.对角线互相平分且相等5.若一次函数![]() 的函数值
的函数值![]() 随
随![]() 的增大而增大,则( )A.
的增大而增大,则( )A.![]() B.
B.![]() C.
C.![]() D.
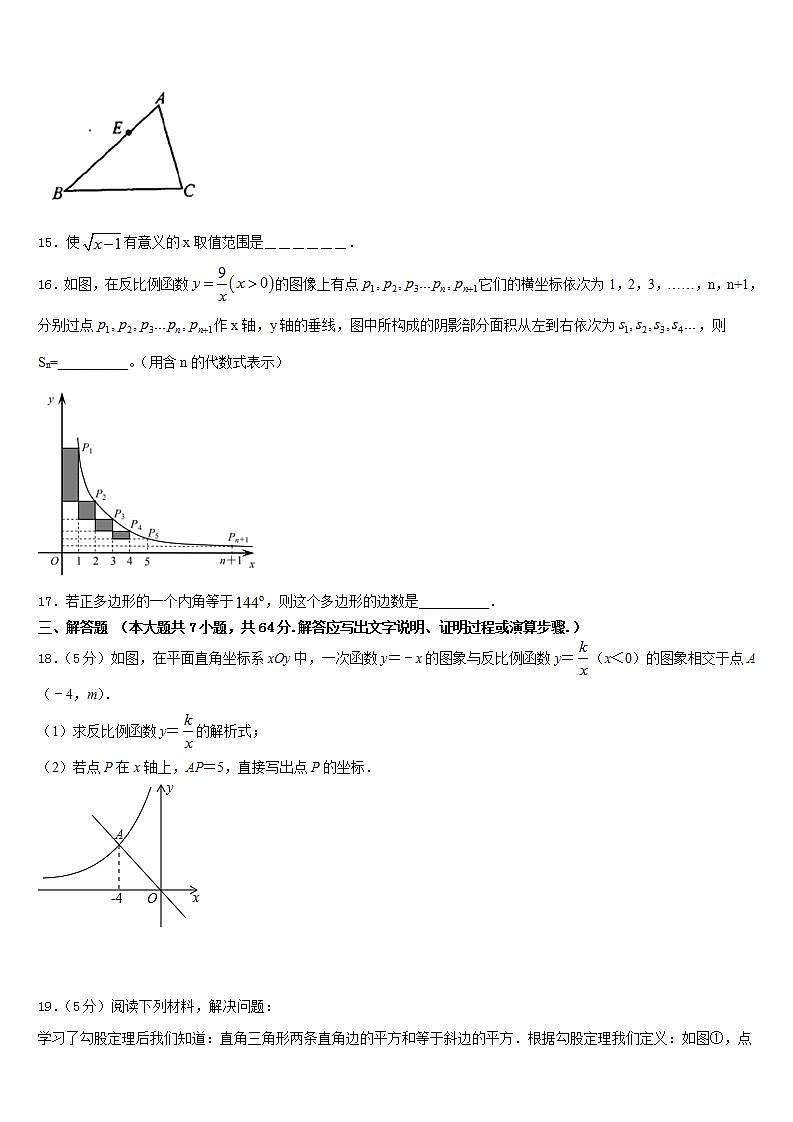
D.![]() 6.如图,在△ABC中,∠B=45°,∠ACB=60°,AB=16,AD⊥BC,垂足为D,∠ACB的平分线交AD于点E,则AE的长为( )
6.如图,在△ABC中,∠B=45°,∠ACB=60°,AB=16,AD⊥BC,垂足为D,∠ACB的平分线交AD于点E,则AE的长为( )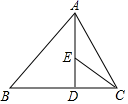 A.
A.![]() B.4
B.4![]() C.
C.![]()
![]() D.6
D.6![]() 7.□ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )A.BE=DF B.AE=CF C.AF//CE D.∠BAE=∠DCF8.某厂接到加工720件衣服的订单,预计每天做48件,正好按时完成,后因客户要求提前5天交货,设每天应多做x件,则x应满足的方程为( )A.
7.□ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )A.BE=DF B.AE=CF C.AF//CE D.∠BAE=∠DCF8.某厂接到加工720件衣服的订单,预计每天做48件,正好按时完成,后因客户要求提前5天交货,设每天应多做x件,则x应满足的方程为( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 9.若代数式
9.若代数式![]() 在实数范围内有意义,则x的取值范围是( )A.x≥﹣2 B.x>﹣2 C.x≥2 D.x≤210.甲、乙二人做某种机械零件,已知甲每小时比乙少做6个,甲做60个所用时间与乙做90个所用时间相等,求甲、乙每小时各做零件多少个.如果设甲每小时做x个,那么所列方程是( )A.
在实数范围内有意义,则x的取值范围是( )A.x≥﹣2 B.x>﹣2 C.x≥2 D.x≤210.甲、乙二人做某种机械零件,已知甲每小时比乙少做6个,甲做60个所用时间与乙做90个所用时间相等,求甲、乙每小时各做零件多少个.如果设甲每小时做x个,那么所列方程是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 11.
11.![]() 的三边长分别为
的三边长分别为![]() ,下列条件:①
,下列条件:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 其中能判断
其中能判断![]() 是直角三角形的个数有( )A.
是直角三角形的个数有( )A.![]() 个 B.
个 B.![]() 个 C.
个 C.![]() 个 D.
个 D.![]() 个12.如图,将一根长为24cm的筷子,置于底面直径为5cm,高为12cm的圆柱水杯中,设筷子露在杯子外面的长度为hcm,则h的取值范围是( )
个12.如图,将一根长为24cm的筷子,置于底面直径为5cm,高为12cm的圆柱水杯中,设筷子露在杯子外面的长度为hcm,则h的取值范围是( )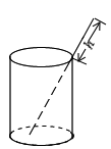 A.12cm≤h≤19cm B.12cm≤h≤13cm C.11cm≤h≤12cm D.5cm≤h≤12cm二、填空题(每题4分,满分20分,将答案填在答题纸上)13.如图,在矩形纸片
A.12cm≤h≤19cm B.12cm≤h≤13cm C.11cm≤h≤12cm D.5cm≤h≤12cm二、填空题(每题4分,满分20分,将答案填在答题纸上)13.如图,在矩形纸片![]() 中,
中,![]() ,
,![]() 折叠纸片,使点
折叠纸片,使点![]() 落在
落在![]() 边上的点
边上的点![]() 处,折痕为
处,折痕为![]() ,当点
,当点![]() 在
在![]() 边上移动时,折痕的端点
边上移动时,折痕的端点![]() ,
,![]() 也随之移动,若限定点
也随之移动,若限定点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 边上移动,则点
边上移动,则点![]() 在
在![]() 边上可移动的最大距离为__________.
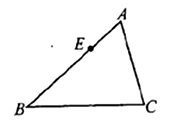
边上可移动的最大距离为__________.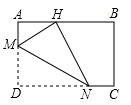 14.如图,在
14.如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() ,点
,点![]() 在
在![]() 上,连结
上,连结![]() ,若
,若![]() 与
与![]() 相似,则
相似,则![]() _____________.
_____________. 15.使
15.使![]() 有意义的x取值范围是______.16.如图,在反比例函数
有意义的x取值范围是______.16.如图,在反比例函数![]() 的图像上有点
的图像上有点![]() 它们的横坐标依次为1,2,3,……,n,n+1,分别过点
它们的横坐标依次为1,2,3,……,n,n+1,分别过点![]() 作x轴,y轴的垂线,图中所构成的阴影部分面积从左到右依次为
作x轴,y轴的垂线,图中所构成的阴影部分面积从左到右依次为![]() ,则Sn=__________。(用含n的代数式表示)
,则Sn=__________。(用含n的代数式表示)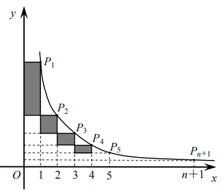 17.若正多边形的一个内角等于
17.若正多边形的一个内角等于![]() ,则这个多边形的边数是__________.三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)如图,在平面直角坐标系xOy中,一次函数y=﹣x的图象与反比例函数y=
,则这个多边形的边数是__________.三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)如图,在平面直角坐标系xOy中,一次函数y=﹣x的图象与反比例函数y=![]() (x<0)的图象相交于点A(﹣4,m).(1)求反比例函数y=
(x<0)的图象相交于点A(﹣4,m).(1)求反比例函数y=![]() 的解析式;(2)若点P在x轴上,AP=5,直接写出点P的坐标.
的解析式;(2)若点P在x轴上,AP=5,直接写出点P的坐标.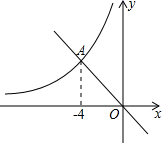 19.(5分)阅读下列材料,解决问题:学习了勾股定理后我们知道:直角三角形两条直角边的平方和等于斜边的平方.根据勾股定理我们定义:如图①,点M、N是线段AB上两点,如果线段AM、MN、NB能构成直角三角形,则称点M、N是线段AB的勾股点解决问题(1)在图①中,如果AM=2,MN=3,则NB= .(2)如图②,已知点C是线段AB上一定点(AC<BC),在线段AB上求作一点D,使得C、D是线段AB的勾股点.李玉同学是这样做的:过点C作直线GH⊥AB,在GH上截取CE=AC,连接BE,作BE的垂直平分线交AB于点D,则C、D是线段AB的勾股点你认为李玉同学的做法对吗?请说明理由(3)如图③,DE是△ABC的中位线,M、N是AB边的勾股点(AM<MN<NB),连接CM、CN分别交DE于点G、H求证:G、H是线段DE的勾股点.
19.(5分)阅读下列材料,解决问题:学习了勾股定理后我们知道:直角三角形两条直角边的平方和等于斜边的平方.根据勾股定理我们定义:如图①,点M、N是线段AB上两点,如果线段AM、MN、NB能构成直角三角形,则称点M、N是线段AB的勾股点解决问题(1)在图①中,如果AM=2,MN=3,则NB= .(2)如图②,已知点C是线段AB上一定点(AC<BC),在线段AB上求作一点D,使得C、D是线段AB的勾股点.李玉同学是这样做的:过点C作直线GH⊥AB,在GH上截取CE=AC,连接BE,作BE的垂直平分线交AB于点D,则C、D是线段AB的勾股点你认为李玉同学的做法对吗?请说明理由(3)如图③,DE是△ABC的中位线,M、N是AB边的勾股点(AM<MN<NB),连接CM、CN分别交DE于点G、H求证:G、H是线段DE的勾股点.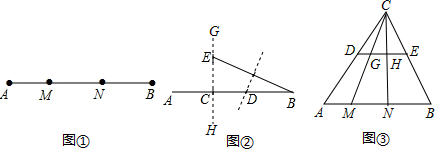 20.(8分)已知点A(2,0)在函数y=kx+3的图象上,(1)求该函数的表达式;(2)求该函数图象与坐标轴围成的三角形的面积. 21.(10分)如图,矩形
20.(8分)已知点A(2,0)在函数y=kx+3的图象上,(1)求该函数的表达式;(2)求该函数图象与坐标轴围成的三角形的面积. 21.(10分)如图,矩形![]() 的对角线
的对角线![]() 垂直平分线与边
垂直平分线与边![]() 、
、![]() 分别交于点
分别交于点![]() ,求证:四边形
,求证:四边形![]() 为菱形.
为菱形. 22.(10分)如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,过点E作EF∥CD交BC的延长线于点F,连接CD.(1)求证:DE=CF;(2)求EF的长.
22.(10分)如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,过点E作EF∥CD交BC的延长线于点F,连接CD.(1)求证:DE=CF;(2)求EF的长.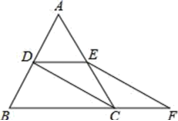 23.(12分)已知某服装厂现有
23.(12分)已知某服装厂现有![]() 种布料70米,
种布料70米,![]() 种布料52米,现计划用这两种布料生产
种布料52米,现计划用这两种布料生产![]() 、
、![]() 两种型号的时装共80套.已知做一套
两种型号的时装共80套.已知做一套![]() 型号的时装需用A种布料1.1米,
型号的时装需用A种布料1.1米,![]() 种布料0.4米,可获利50元;做一套
种布料0.4米,可获利50元;做一套![]() 型号的时装需用
型号的时装需用![]() 种布料0.6米,
种布料0.6米,![]() 种布料0.9米,可获利45元.设生产
种布料0.9米,可获利45元.设生产![]() 型号的时装套数为
型号的时装套数为![]() ,用这批布料生产两种型号的时装所获得的总利润为
,用这批布料生产两种型号的时装所获得的总利润为![]() 元.(1)求
元.(1)求![]() (元)与
(元)与![]() (套)的函数关系式.(2)有几种生产方案?(3)如何生产使该厂所获利润最大?最大利润是多? 参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、A2、D3、C4、B5、B6、C7、B8、D9、C10、A11、C12、C 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、114、2或4.515、x≥116、
(套)的函数关系式.(2)有几种生产方案?(3)如何生产使该厂所获利润最大?最大利润是多? 参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、A2、D3、C4、B5、B6、C7、B8、D9、C10、A11、C12、C 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、114、2或4.515、x≥116、![]() 17、十 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、(1)y=﹣
17、十 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、(1)y=﹣![]() ;(2)P点的坐标是(﹣7,0)或(﹣1,0).19、(1)
;(2)P点的坐标是(﹣7,0)或(﹣1,0).19、(1)![]() 或
或![]() ;(2)对,理由见解析;(3)见解析20、 (1)y=-
;(2)对,理由见解析;(3)见解析20、 (1)y=-![]() x+3(3)3 21、见解析22、 (1)见解析;(2)
x+3(3)3 21、见解析22、 (1)见解析;(2)![]() .23、(1)y=5x+3600;(2)共有5种生产方案;(3)当生产
.23、(1)y=5x+3600;(2)共有5种生产方案;(3)当生产![]() 型号的时装44套、生产
型号的时装44套、生产![]() 型号的时装36套时,该厂所获利润最大,最大利润为3820元.
型号的时装36套时,该厂所获利润最大,最大利润为3820元.
相关试卷
这是一份云南省曲靖市罗平县2023-2024学年九上数学期末复习检测试题含答案,共8页。试卷主要包含了考生必须保证答题卡的整洁,关于抛物线,下列说法错误的是等内容,欢迎下载使用。
这是一份云南省曲靖市2022-2023学年七下数学期末学业质量监测试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,下列命题等内容,欢迎下载使用。
这是一份云南省罗平县联考2022-2023学年数学七年级第二学期期末检测模拟试题含答案,共7页。试卷主要包含了答题时请按要求用笔,如图,设线段AC=1等内容,欢迎下载使用。










