


2022-2023学年云南省云南师范大附属中学七年级数学第二学期期末检测试题含答案
展开
这是一份2022-2023学年云南省云南师范大附属中学七年级数学第二学期期末检测试题含答案,共8页。
2022-2023学年云南省云南师范大附属中学七年级数学第二学期期末检测试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 请考生注意:1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。 一、选择题(每小题3分,共30分)1.下表是小红填写的实践活动报告的部分内容: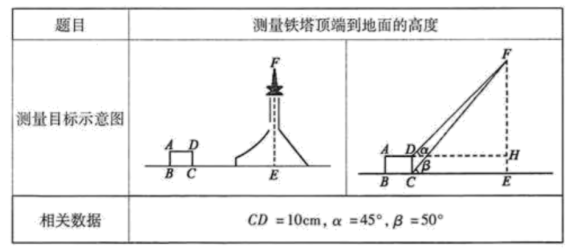 设铁塔顶端到地面的高度
设铁塔顶端到地面的高度![]() 为
为![]() ,根据以上条件,可以列出的方程为( )A.
,根据以上条件,可以列出的方程为( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 2.小华所在的九年级一班共有50名学生,一次体检测量了全班学生的身高,由此求得该班学生的平均身高是1.65米,而小华的身高是1.66米,下列说法错误的是( )A.1.65米是该班学生身高的平均水平B.班上比小华高的学生人数不会超过25人C.这组身高数据的中位数不一定是1.65米D.这组身高数据的众数不一定是1.65米3.不等式组
2.小华所在的九年级一班共有50名学生,一次体检测量了全班学生的身高,由此求得该班学生的平均身高是1.65米,而小华的身高是1.66米,下列说法错误的是( )A.1.65米是该班学生身高的平均水平B.班上比小华高的学生人数不会超过25人C.这组身高数据的中位数不一定是1.65米D.这组身高数据的众数不一定是1.65米3.不等式组![]() 的解集是( )A.
的解集是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 4.在
4.在![]() 中,点
中,点![]() 、
、![]() 分别为边
分别为边![]() 、
、![]() 的中点,则
的中点,则![]() 与
与![]() 的面积之比为
的面积之比为![]()
![]() A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 5.小黄在自家种的西瓜地里随意称了10个西瓜,重量(单位:斤)分别是:5,8,6,8,10,1,1,1,7,1.按市场价西瓜每斤2元的价格计算,你估算一下,小黄今天卖了350个西瓜约收入( )A.160元 B.700元 C.5600 D.70006.在同一坐标系中,函数y=kx与y=3x﹣k的图象大致是( )A.
5.小黄在自家种的西瓜地里随意称了10个西瓜,重量(单位:斤)分别是:5,8,6,8,10,1,1,1,7,1.按市场价西瓜每斤2元的价格计算,你估算一下,小黄今天卖了350个西瓜约收入( )A.160元 B.700元 C.5600 D.70006.在同一坐标系中,函数y=kx与y=3x﹣k的图象大致是( )A.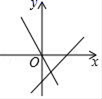 B.
B.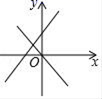 C.
C.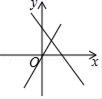 D.
D.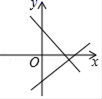 7.多项式4x2﹣4与多项式x2﹣2x+1的公因式是( )A.x﹣1 B.x+1 C.x2﹣1 D.(x﹣1)28.下列等式中,从左到右的变形是因式分解的是( )A.
7.多项式4x2﹣4与多项式x2﹣2x+1的公因式是( )A.x﹣1 B.x+1 C.x2﹣1 D.(x﹣1)28.下列等式中,从左到右的变形是因式分解的是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 9.点(3,-4)到x轴的距离为 ( )A.3 B.4 C.5 D.-410.如图在平面直角坐标系
9.点(3,-4)到x轴的距离为 ( )A.3 B.4 C.5 D.-410.如图在平面直角坐标系![]() 中若菱形
中若菱形![]() 的顶点
的顶点![]() 的坐标分别为
的坐标分别为![]() ,点
,点![]() 在
在![]() 轴上,则点
轴上,则点![]() 的坐标是( )
的坐标是( )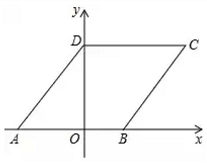 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 二、填空题(本大题共有6小题,每小题3分,共18分)11.将直线y=2x+1向下平移3个单位长度后所得直线的表达式是 ______.12.已知一元二次方程
二、填空题(本大题共有6小题,每小题3分,共18分)11.将直线y=2x+1向下平移3个单位长度后所得直线的表达式是 ______.12.已知一元二次方程![]() 的两个解恰好分别是等腰
的两个解恰好分别是等腰![]() 的底边长和腰长,则
的底边长和腰长,则![]() 的周长为__________.13.如图所示,在△ABC中,∠B=90°,AB=3,AC=5,将△ABC折叠,使点C与点A重合,折痕为DE,则△ABE的周长为 .
的周长为__________.13.如图所示,在△ABC中,∠B=90°,AB=3,AC=5,将△ABC折叠,使点C与点A重合,折痕为DE,则△ABE的周长为 .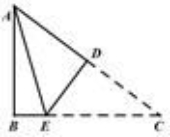 14.已知△ABC的周长为4,顺次连接△ABC三边的中点构成的新三角形的周长为__________.15.评定学生的学科期末成绩由考试分数,作业分数,课堂参与分数三部分组成,并按3:2:5的比例确定,已知小明的数学考试90分,作业95分,课堂参与92分,则他的数学期末成绩为_____.16.若关于
14.已知△ABC的周长为4,顺次连接△ABC三边的中点构成的新三角形的周长为__________.15.评定学生的学科期末成绩由考试分数,作业分数,课堂参与分数三部分组成,并按3:2:5的比例确定,已知小明的数学考试90分,作业95分,课堂参与92分,则他的数学期末成绩为_____.16.若关于![]() 的一次函数
的一次函数![]() (
(![]() 为常数)中,
为常数)中,![]() 随
随![]() 的增大而减小,则
的增大而减小,则![]() 的取值范围是____.三、解下列各题(本大题共8小题,共72分)17.(8分)如图,一次函数y=kx+b的图象经过点A(8,0),直线y=-3x+6与x轴交于点B,与y轴交于点D,且两直线交于点C(4,m).
的取值范围是____.三、解下列各题(本大题共8小题,共72分)17.(8分)如图,一次函数y=kx+b的图象经过点A(8,0),直线y=-3x+6与x轴交于点B,与y轴交于点D,且两直线交于点C(4,m).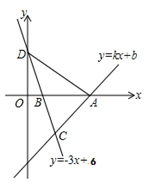 (1)求m的值及一次函数的解析式;(2)求△ACD的面积. 18.(8分)计算:(1)
(1)求m的值及一次函数的解析式;(2)求△ACD的面积. 18.(8分)计算:(1)![]() (2)
(2)![]() 19.(8分)解方程:
19.(8分)解方程: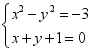 20.(8分)某市篮球队在市一中选拔一名队员.教练对王亮和李刚两名同学进行5次3分投篮测试,每人每次投10个球,如图记录的是这两名同学5次投篮中所投中的个数.
20.(8分)某市篮球队在市一中选拔一名队员.教练对王亮和李刚两名同学进行5次3分投篮测试,每人每次投10个球,如图记录的是这两名同学5次投篮中所投中的个数.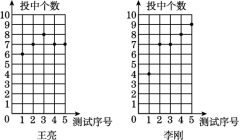 姓名平均数(个)众数(个)方差王亮7 李刚 72.8(1)请你根据图中的数据,填写上表.(2)你认为谁的成绩比较稳定,为什么?(3)若你是教练,你打算选谁?简要说明理由. 21.(8分)为了加强公民的节水意识,合理利用水资源,各地采取价格调控手段达到节约用水的目的,某市规定如下用水收费标准:每户每月的用水量不超过
姓名平均数(个)众数(个)方差王亮7 李刚 72.8(1)请你根据图中的数据,填写上表.(2)你认为谁的成绩比较稳定,为什么?(3)若你是教练,你打算选谁?简要说明理由. 21.(8分)为了加强公民的节水意识,合理利用水资源,各地采取价格调控手段达到节约用水的目的,某市规定如下用水收费标准:每户每月的用水量不超过![]() 立方米时,水费按每立方米
立方米时,水费按每立方米![]() 元收费,超过
元收费,超过![]() 立方米时,不超过的部分每立方米仍按
立方米时,不超过的部分每立方米仍按![]() 元收费,超过的部分每立方米按
元收费,超过的部分每立方米按![]() 元收费,该市某户今年
元收费,该市某户今年![]() 月份的用水量和所交水费如下表所示:月份用水量(
月份的用水量和所交水费如下表所示:月份用水量(![]() )收费(元)
)收费(元)![]()
![]()
![]()
![]()
![]()
![]() 设某户每月用水量
设某户每月用水量![]() (立方米),应交水费
(立方米),应交水费![]() (元)
(元)![]() 求
求![]() 的值,当
的值,当![]() 时,分别写出
时,分别写出![]() 与
与![]() 的函数关系式.
的函数关系式.![]() 若该户
若该户![]() 月份用水量为
月份用水量为![]() 立方米,求该
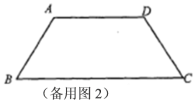
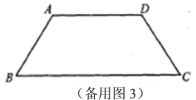
立方米,求该![]() 月份水费多少元? 22.(10分)如图,在等腰梯形ABCD中,
月份水费多少元? 22.(10分)如图,在等腰梯形ABCD中,![]() ,
,![]() ,
,![]() ,
,![]() .点Р从点B出发沿折线段
.点Р从点B出发沿折线段![]() 以每秒5个单位长的速度向点C匀速运动;点Q从点C出发沿线段CB方向以每秒3个单位长的速度匀速运动,过点O向上作射线OKIBC,交折线段
以每秒5个单位长的速度向点C匀速运动;点Q从点C出发沿线段CB方向以每秒3个单位长的速度匀速运动,过点O向上作射线OKIBC,交折线段![]()
![]() 于点E.点P、O同时开始运动,为点Р与点C重合时停止运动,点Q也随之停止.设点P、Q运动的时间是t秒
于点E.点P、O同时开始运动,为点Р与点C重合时停止运动,点Q也随之停止.设点P、Q运动的时间是t秒![]() .(1)点P到达终点C时,求t的值,并指出此时BQ的长;(2)当点Р运动到AD上时,t为何值能使
.(1)点P到达终点C时,求t的值,并指出此时BQ的长;(2)当点Р运动到AD上时,t为何值能使![]() ?(3)t为何值时,四点P、Q、C、E成为一个平行四边形的顶点?(4)
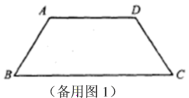
?(3)t为何值时,四点P、Q、C、E成为一个平行四边形的顶点?(4)![]() 能为直角三角形时t的取值范围________.(直接写出结果)(注:备用图不够用可以另外画)
能为直角三角形时t的取值范围________.(直接写出结果)(注:备用图不够用可以另外画)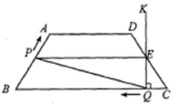
 23.(10分)如图,在平面直角坐标系中,直线y=2x+4与x轴交于点A,与y轴交于点B,过点B的直线交x轴于C,且△ABC面积为1.
23.(10分)如图,在平面直角坐标系中,直线y=2x+4与x轴交于点A,与y轴交于点B,过点B的直线交x轴于C,且△ABC面积为1.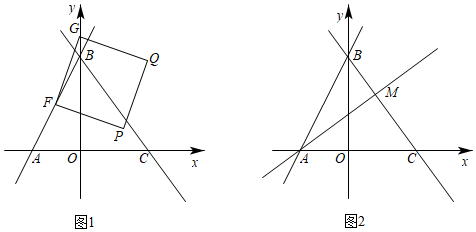 (1)求点C的坐标及直线BC的解析式;(2)如图1,设点F为线段AB中点,点G为y轴上一动点,连接FG,以FG为边向FG右侧作正方形FGQP,在G点的运动过程中,当顶点Q落在直线BC上时,求点G的坐标;(3)如图2,若M为线段BC上一点,且满足S△AMB=S△AOB,点E为直线AM上一动点,在x轴上是否存在点D,使以点D,E,B,C为顶点的四边形为平行四边形?若存在,请直接写出点D的坐标;若不存在,请说明理由. 24.(12分)已知:正方形ABCD,E为平面内任意一点,连接DE,将线段DE绕点D顺时针旋转90°得到DG,连接EC,AG.(1)当点E在正方形ABCD内部时,①根据题意,在图1中补全图形;②判断AG与CE的数量关系与位置关系并写出证明思路.(2)当点B,D,G在一条直线时,若AD=4,DG=
(1)求点C的坐标及直线BC的解析式;(2)如图1,设点F为线段AB中点,点G为y轴上一动点,连接FG,以FG为边向FG右侧作正方形FGQP,在G点的运动过程中,当顶点Q落在直线BC上时,求点G的坐标;(3)如图2,若M为线段BC上一点,且满足S△AMB=S△AOB,点E为直线AM上一动点,在x轴上是否存在点D,使以点D,E,B,C为顶点的四边形为平行四边形?若存在,请直接写出点D的坐标;若不存在,请说明理由. 24.(12分)已知:正方形ABCD,E为平面内任意一点,连接DE,将线段DE绕点D顺时针旋转90°得到DG,连接EC,AG.(1)当点E在正方形ABCD内部时,①根据题意,在图1中补全图形;②判断AG与CE的数量关系与位置关系并写出证明思路.(2)当点B,D,G在一条直线时,若AD=4,DG=![]() ,求CE的长.(可在备用图中画图)
,求CE的长.(可在备用图中画图)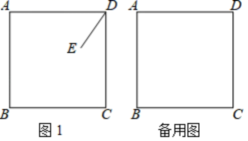 参考答案 一、选择题(每小题3分,共30分)1、A2、B3、A4、C5、C6、B7、A8、D9、B10、B 二、填空题(本大题共有6小题,每小题3分,共18分)11、y=1x-112、213、114、215、9216、
参考答案 一、选择题(每小题3分,共30分)1、A2、B3、A4、C5、C6、B7、A8、D9、B10、B 二、填空题(本大题共有6小题,每小题3分,共18分)11、y=1x-112、213、114、215、9216、![]() 三、解下列各题(本大题共8小题,共72分)17、(1)一次函数的解析式为y=
三、解下列各题(本大题共8小题,共72分)17、(1)一次函数的解析式为y=![]() x-12(2)3618、(1)
x-12(2)3618、(1)![]() ; (2)
; (2)![]() 19、
19、![]() 20、 (1)从左到右依次填7,7,0.4;(2)王亮的成绩比较稳定;(3)选王亮,理由见解析.21、(1)y=6x-27;(2)
20、 (1)从左到右依次填7,7,0.4;(2)王亮的成绩比较稳定;(3)选王亮,理由见解析.21、(1)y=6x-27;(2)![]() 元.22、 (2)
元.22、 (2) ![]() 秒,
秒,![]() ;(2)详见解析;(3)
;(2)详见解析;(3)![]() ;(4)
;(4)![]() 或
或![]() .23、(1)C(3,0),直线BC的解析式为y=﹣
.23、(1)C(3,0),直线BC的解析式为y=﹣![]() x+4;(2)满足条件的点G坐标为(0,
x+4;(2)满足条件的点G坐标为(0,![]() )或(0,﹣1);(3)存在,满足条件的点D的坐标为(
)或(0,﹣1);(3)存在,满足条件的点D的坐标为(![]() ,0)或(﹣
,0)或(﹣![]() ,0)或(﹣
,0)或(﹣![]() ,0)24、 (1) ①见解析;②AG=CE,AG⊥CE,理由见解析;(2)CE的长为
,0)24、 (1) ①见解析;②AG=CE,AG⊥CE,理由见解析;(2)CE的长为![]() 或
或![]()
相关试卷
这是一份云南省云南师范大附属中学2023-2024学年九上数学期末达标测试试题含答案,共7页。试卷主要包含了下列计算错误的是等内容,欢迎下载使用。
这是一份云南省昆明市云南师范大附属中学2023-2024学年九年级数学第一学期期末检测模拟试题含答案,共8页。试卷主要包含了计算的结果是等内容,欢迎下载使用。
这是一份云南省昆明市云南师范大附属中学2023-2024学年八年级数学第一学期期末检测试题含答案,共7页。试卷主要包含了点P关于x轴的对称点的坐标为等内容,欢迎下载使用。










